Lab 02: Graphics + Recursion = Fractals

DUE: Friday, February 26, 23:59 AOE

Prerequisites

• Read Chapter 10 of Java Programming on recursion.

• Read the notes Recursive Fractals

• Read the notes A Recursive Image

• Download, compile, and run RecursiveSquares.java.

Your Assignment

For this lab, you will write a program that generates four variations of a fractal consisting of overlapping squares. The final output should look something like this:

The square figures are generated in the following manner: each time a square is drawn, four smaller squares are also drawn: one centered at the square’s four corners. The relative size of the smaller squares should controlled using the variable SQUARE_RATIO, which is set to 2.2 by default. Thus, if the central has width 200 pixels, the squares placed on its corners will have width 200 / 2.2 = 91 pixels (note that all dimensions should be ints).

In addition to drawing the “default” image, your program should take a command line argument that allows the user to specify the depth of the image. The supplied code in RecursiveSquares.java already reads an integer input (if supplied by the user) and stores it as a variable private int depth:

1
2
3
        if (args.length > 0) {
            depth = Integer.parseInt(args[0]);
        }

To specify a recursion depth, you should run the program with an integer following the usual execution command:

1
    java RecursiveSquares 2

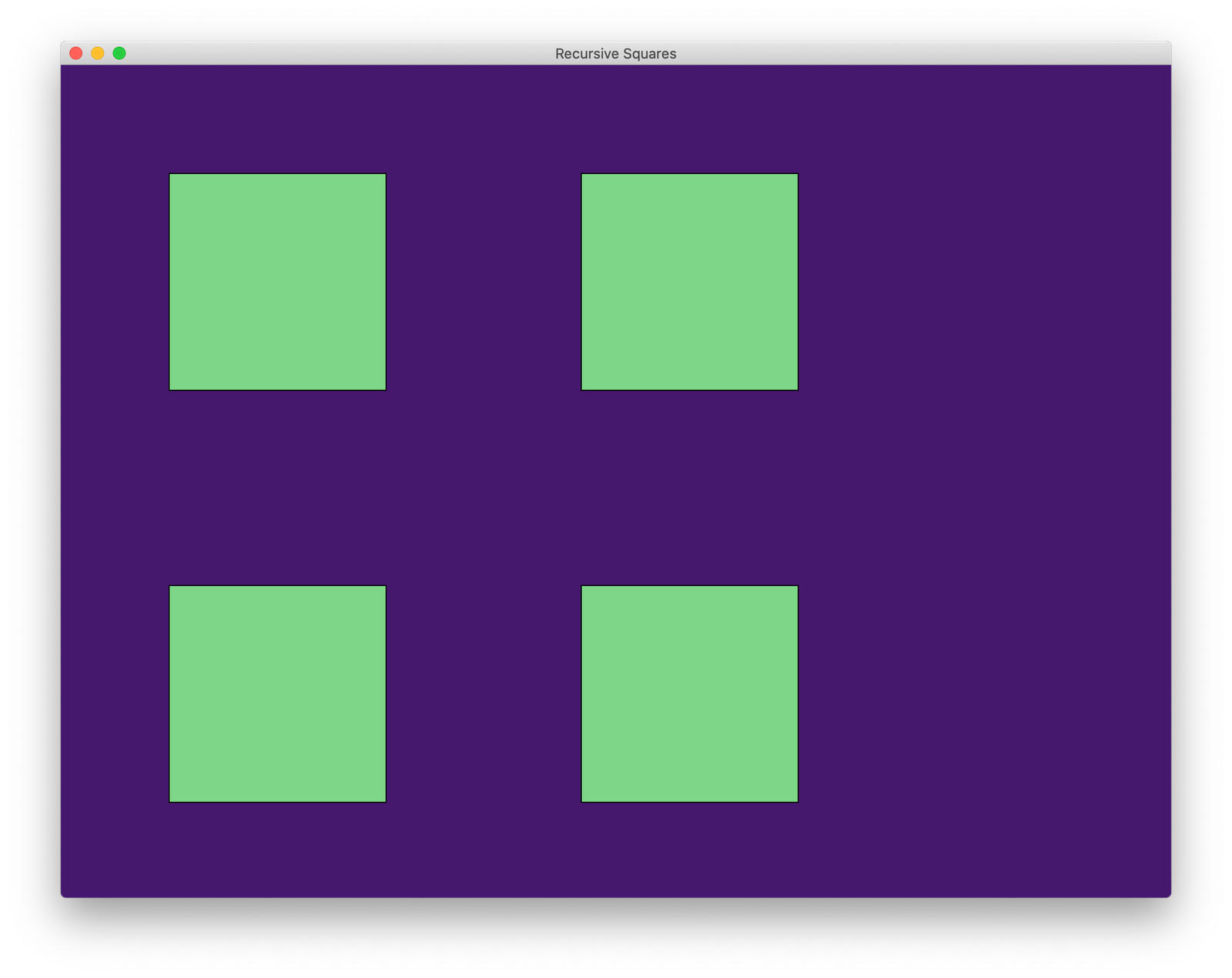
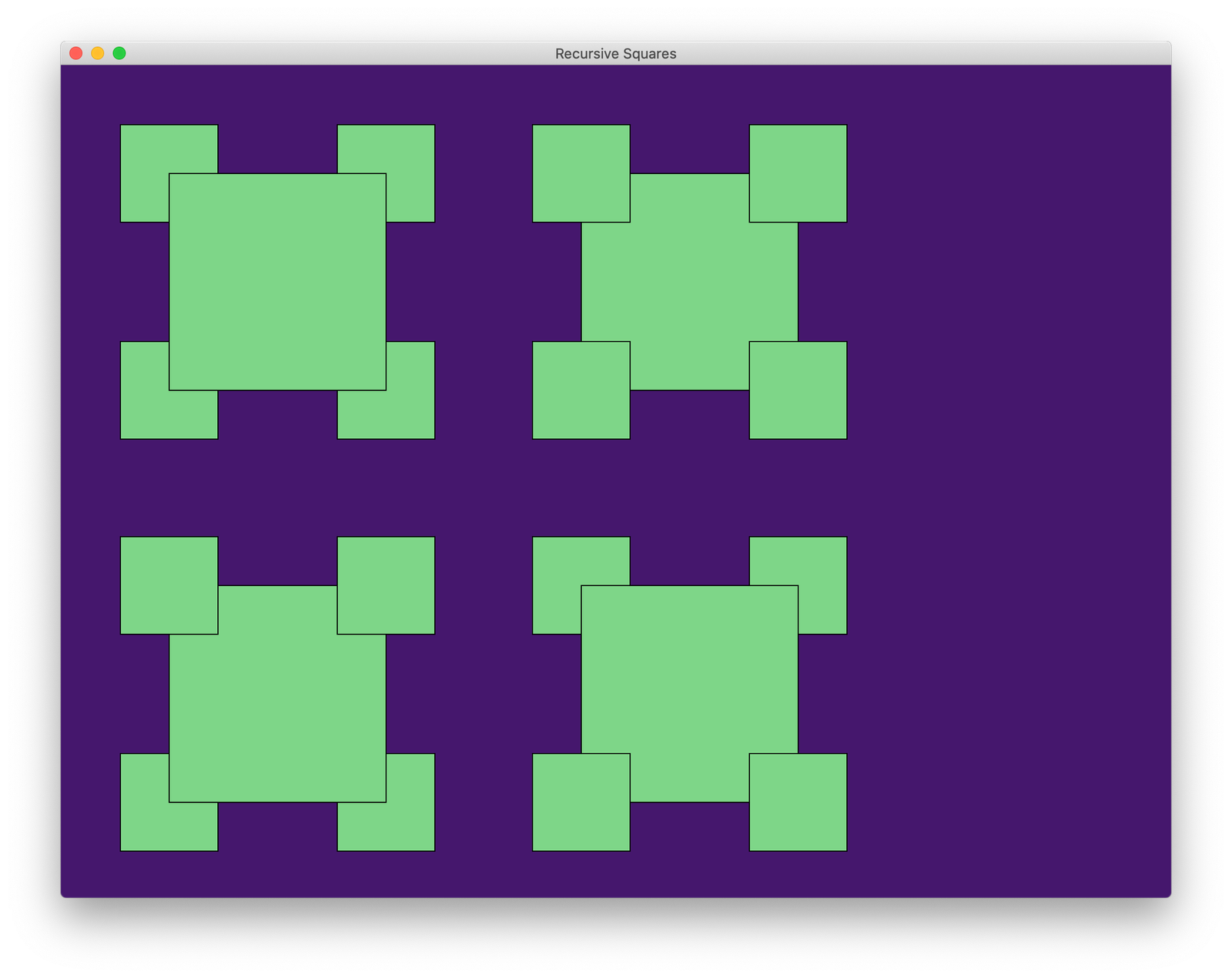
For example, the following three images show the desired outputs for

1
2
3
    java RecursiveSquares 0
    java RecursiveSquares 1
    java RecursiveSquares 2

respectively.

Suggestions

1. Start simple. First, define a method that draws a single square. Note that to draw an outlined square (as in the figures above), you must draw the interior and boundary separately. Look at the Graphics documentation to figure out how.

2. First figure out how to draw the upper left figure in the images above, then figure out how to modify the code to draw the other three figures. You should only need very small modifications to the code once you can draw the upper left figure!

3. Use recursion! Once you can draw a single square, drawing the complete figure recursively should require a very small amount of code (think less than 10 lines per figure).

4. Figure out how to control the depth of recursion. When does a recursive call to a function know it is “done” (i.e., shouldn’t make further recursive calls)?. Be sure to use the variable depth in the provided code.

Extensions

There are a lot of ways to extend this assignment. Here are a few suggestions, but don’t feel constrained to doing one of this extensions (if any). Just be sure to turn in the basic assignment, as well as your extension if you are doing an extension.

1. Color by depth of recursion. Specifically, pick a color corresponding to the depth of each recursive call, and color all squares at that depth the same color. Here is some example output (drawn without square outlines because it looks better):

   

2. Turn the figure you drew from Lab 01 into a fractal by drawing that figure instead of squares! For example, the dog I drew in my solution turns into the following creepy fractal animal:

   

3. Generate one of the “classic” fractals depicted in the Fractals notes.

4. Generate some other crazy fractals using recursion!

To Turn In

All code should be turned in to the Moodle submission page by 23:59 AoE on Friday, February 26th. (This corresponds to 7:59 am on Saturday February 26th, Eastern Time.) Please upload your own modified copy of RecursiveSquares.java, and separate files for extensions (if any).

Grading

Your basic assignment will be graded on a 3 point scale as follows:

• 3 points. Submission produces the desired output in the manner specified by the assignment. Code is clearly organized with comments describing what different components of the code (e.g., methods) do.

• 2 points. Submission produces more-or-less the desired output, but may diverge from the program description in the assignment. Code is not clearly organized and/or lacking helpful comments.

• 1 point. Submission compiles, but does not produce the desired output. Code is confusingly written without useful comments.

• 0 points. Submission does not compile.

In addition to the points above, you will receive credit for any extenion(s) as specified in the course syllabus.