Recursive Fractals
An introduction to recursively generated fractals.
What are fractals?
Informally, fractals are geometric figures that exhibit self-symmetry: that is, there is a regular structure that repeats on different scales. Visually, they tend to be characterized by intricate repeating patterns. A prototypical example of a fractal is the Sierpinski Triangle, depicted here:
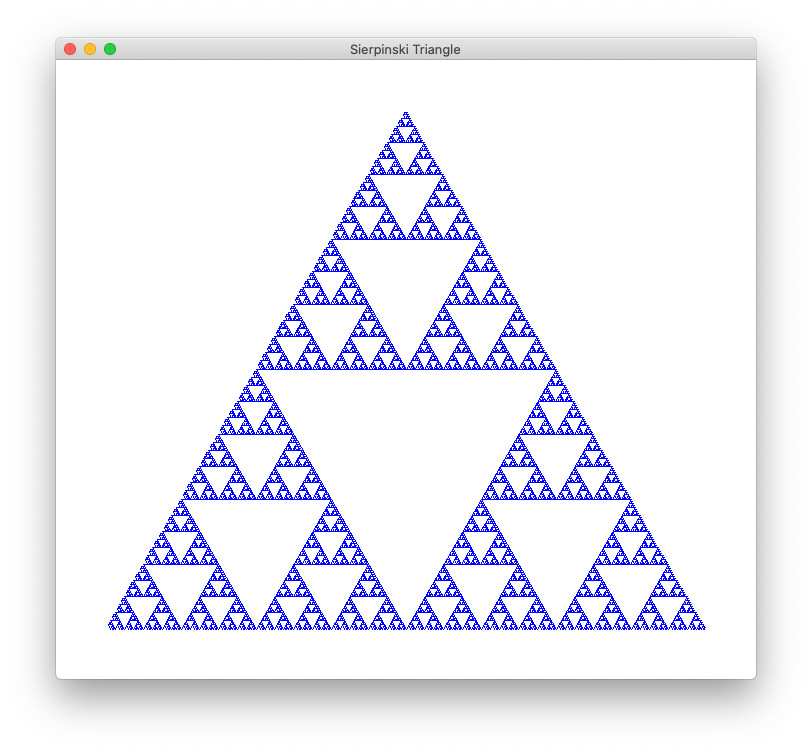
The figure consists of a large triangle broken into 4 triangular parts: central, top, left, and right. The central triangle is white with a blue outline. The other three regions are similar to the whole triangle, but at 1/2 the scale. One can construct the Sierpinski triangle in stages. In the first stage, only the central triangle is drawn. In the second stage, the upper, left, and right triangles are replaced with “copies” of the first stage image, scaled by a factor of 1/2. In the next and subsequent stages, each sub-triangle is further subdivided into 4 regions, with the non-central regions being drawn as scaled-down copies of the first stage image.

Procedurally, we can generate the Sierpinski Triangle recursively: to draw a Sierpinski triangle, first draw the central triangle. Then draw (smaller) Sierpinski triangles in the top, left, and right regions, each of which consists of a scaled-down Sierpinski triangle. Thus, we can draw the Sierpinski triangle to a specified recursion depth. The image above shows generations of this procedure stopped at depths 0, 1, 2, and 3 from left to right.
To turn this idea into code, we need to specify when the procedure is completed—i.e., when the base case is reached. There are two natural ways of doing this:
- Have the user specify a fixed depth of recursion.
- Stop drawing new objects once they become too small to draw (e.g., the scale becomes less than, say, a single pixel).
The previous image was generated using method 1 above, specifying a fixed depth and stopping recursive calls once that depth was reached.
The Koch curve
Another well-known example of a fractal is the Koch curve or Koch snowflake. This curve can be generated as follows. Start with an equilateral triangle. Then each (recursive) step makes the following transformation: replace each line segment with 4 line segments, each 1/3 the length of the previous line segment in the following configuration:
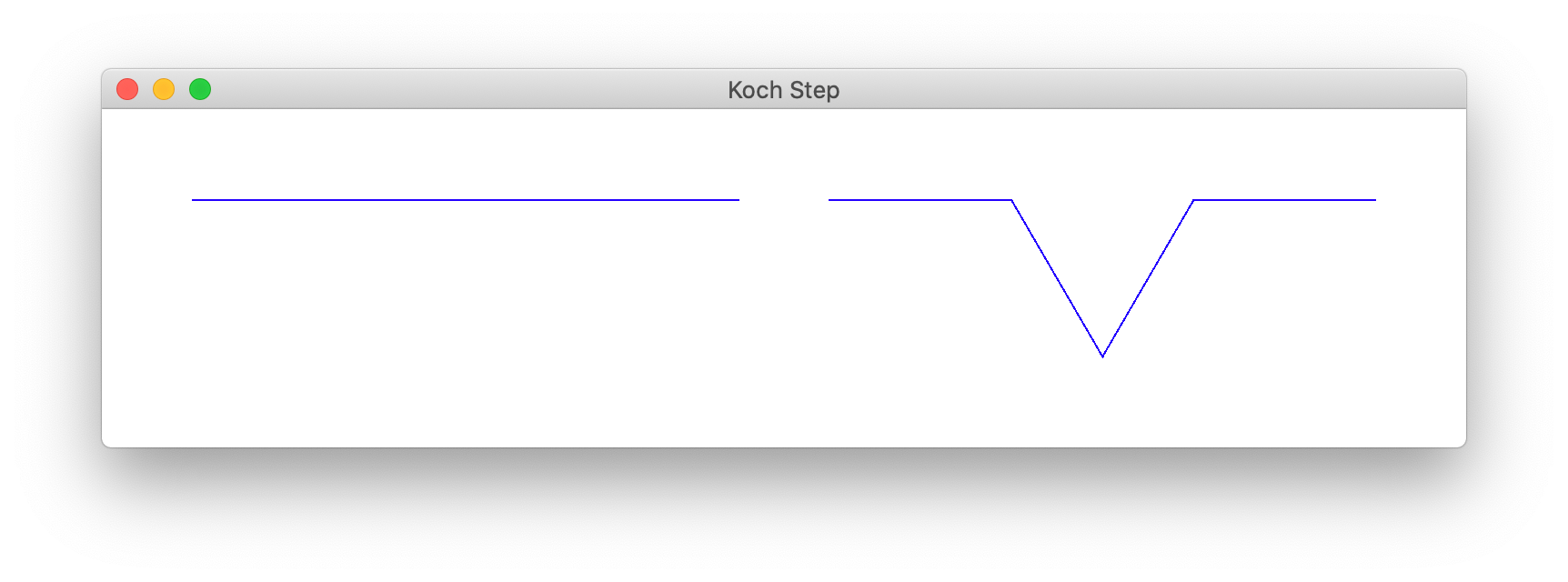
The following figure shows the images generated after applying this procedure to recursion depth 0, 1, 2, and 3, respectively, from left to right.

Applying the same procedure indefinitely (or until the line-segments become smaller than a single pixel), we arrive at the following picture:

General approaches to generating (some) fractals
The two examples above—the Sierpinski triangle and Koch curve—illustrate two general techniques for generating fractals. The first method (which we used to draw the Sierpinski triangle) is to do the following:
- Draw a (simple) figure (e.g., a triangle)
- Recursively draw one or more transformed copies of the same figure (scaled, translated, and/or rotated).
The second method (used to draw the Koch curve) is the following:
- Define a simple figure (e.g., a line segment)
- Subdivide the simple figure, and apply a simple transformation (e.g., turn the line segment into 4 connected segments)
- Recursively apply the subdivision/transformation to each subdivision.
Using these general strategies, you can generate a wide range of intricate, beautiful, and often surprising images. A few other notable examples include:
- Barnsley fern, a fern-like fractal generated by surprisingly simple rules.
- Hilbert curve, a “space filling curve” with surprising applications in geometry and computer science.
- Wiener process, a construction made by choosing an appropriate subdivision of a line and randomly transforming the subdivisions. This random process has been studied for its applications to physics, probability, and even mathematical finance.
IYI: A mathematical aside
While many people are attracted to fractals for their visual properties, fractals have been studied in mathematics for their often surprising and counter-intuitive mathematical features. For example, consider the Koch curve generated above. Suppose we start with an equilateral triangle with side length 1. After a single transformation (recursion depth 1), each side is replaced by 4 line segments, each of length 1/3. Thus the perimeter of the new figure is 4. Similarly, at recursion depth 2, the perimeter increases by a factor of 4/3, so the depth-2 figure has a perimeter of 16/3. Continuing indefinitely, the perimeter increases exponentially, so “in the limit” the Koch curve has an infinite perimeter.
Despite having an infinite perimeter, the region enclosed by the curve is bounded—its area is finite! In fact, a careful calculation shows that the area enclosed is precisely 8/3 times the volume of the original triangle. So the Koch curve gives an example of a figure with infinite perimeter but enclosing only a finite area.