Lab 02: Computing Shortcuts
exploiting parallelism to find shortcuts in a network
DUE: Friday, February 24, 11:59 pm
Background
Suppose we have a network consisting of \(n\) nodes and directed links or edges between each pair of nodes. That is, given nodes \(i\) and \(j\), there is an edge \(e = (i, j)\) from \(i\) to \(j\). For example, the following figure illustrates a network with three nodes, and the arrows indicate the directions of the links: \((i, j)\) is indicated by an arrow from \(i\) to \(j\), while \((j, i)\) is indicated by an arrow from \(j\) to \(i\).
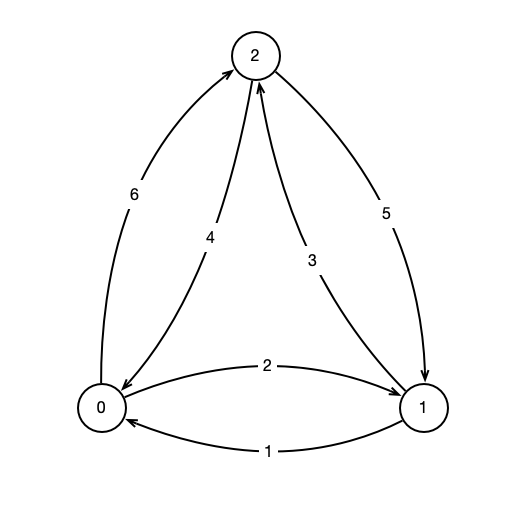
Each edge \((i, j)\) has an associated weight, \(w(i, j)\) that indicates the cost of moving from node \(i\) to node \(j\) along \((i, j)\). The weights of the edges are indicated in the figure above. For example, \(w(0, 1) = 2\). Given the weights of the edges, it might be the case in order to move from \(i\) to \(j\), it would be less expensive to travel via an intermediate node \(k\), i.e. travel from \(i\) to some \(k\), then from \(k\) to \(j\). Traveling in this way, we incur a cost of \(w(i, k) + w(k, j)\). For example, in the figure above, traveling from \(0\) to \(2\) across the edge \((0, 2)\), we incur a cost of \(w(0, 2) = 6\), while traveling from \(0\) to \(1\) to \(2\) has a cost of \(w(0, 1) + w(1, 2) = 2 + 3 = 5\). Thus, the path \(0, 1, 2\) is a shortcut from \(0\) to \(2\).
In this assignment, you will write a program that, given any network and weights, computes the cheapest route between every pair of nodes along a path of length at most 2 (i.e., with at most a single intermediate node).
Network Representation
We assume that the edge weights are positive real numbers (i.e., decimals). For a network with \(n\) nodes labeled, say \(1, 2, \ldots, n\), we must specify the weights \(w(i, j)\) for all \(i, j \leq n\). By convention, we take \(w(i, i) = 0\) for all \(i\). We can represent the network as an \(n \times n\) matrix \(D\)—i.e., a 2 dimensional \(n\) by \(n\) array of numbers. The entry in the \(i\)th row and \(j\)th column, \(d_{ij}\) stores the weight \(w(i, j)\). For example, here is the matrix corresponding to the previous figure:
\[D = \left( \begin{array}{ccc} 0 & 2 & 6\\ 1 & 0 & 3\\ 4 & 5 & 0 \end{array} \right)\]If \(D\) represents the original matrix of weights, then the shortcut distances can also be represented by a matrix \(R\), where the entry \(r_{ij}\) stores the shortcut distance from node \(i\) to \(j\). More formally,
\[r_{ij} = \min_{k} d_{ik} + d_{kj}.\]Notice that by taking \(k = i\), we have \(r_{ij} \leq d_{ii} + d_{ik} = d_{ik}\), because we assume \(d_{ii} = 0\). Using the \(D\) from our previous example, we compute the corresponding \(R\):
\[R = \left( \begin{array}{ccc} 0 & 2 & 5\\ 1 & 0 & 3\\ 4 & 5 & 0 \end{array} \right).\]Notice that \(D\) and \(R\) are the same, except that \(d_{0, 2} = 6\), while \(r_{0, 2} = 5\). This corresponds to the shortcut \(0 \to 1 \to 2\) which has weight \(5\).
Internally, we can represent the original matrix as a two dimensional array of floats, e.g., with float[][] matrix = new float[n][n];. For the previous examples, we’d store \(D\) as follows.
1
2
3
[[0.0, 2.0, 6.0],
[1.0, 0.0, 3.0],
[4.0, 5.0, 0.0]]
A Note on Efficiency
Given an \(n \times n\) matrix \(D\), the resulting shortcut matrix \(R\) can be computed by taking the minimum \(r_{i j} = \min_{k} d_{i k} + d_{k j}\) directly. For each pair \(i, j \leq n\), taking this minimum requires \(n\) additions and comparisons: one addition and comparison for each value of \(k\). Thus the total number of elementary operations (floating point arithmetic, comparisons, etc.) is \(O(n^3)\). Therefore, even for a fairly modest network size of \(n \approx 1,000\), we already need billions of elementary operations. For a network of size 10,000, we need to perform trillions of operations. For reference, the network of city streets in New York City contains approximately 12,500 intersections with traffic signals (i.e., nodes), so naively computing shortcuts for New York would already require trillions of operations. (The structure of New York City streets allows for more efficient means of computing shortcuts, but this example shows the scale of a real-world application to finding shorter routes, say, for driving directions.)
Program Description
For this assignment, you will write a program that, given a matrix \(D\) (i.e., 2d array) of non-negative weights of edges, computes the shortcut matrix \(R\) as described above. Specifically, you will complete an implementation of the SquareMatrix class provided below by writing a method getShortcutMatrixOptimized(), that returns a SquareMatrix instance representing the shortcut matrix of this instance. To get started, download lab02-shortcuts.zip:
The archive contains three files: SquareMatrix.java, ShortcutTester.java, and run-test.sh.
-
SquareMatrix.javaprovides two main methods, as well as some auxiliary methods for creating and comparing matrices:-
getShortcutMatrixBaseline()gives a baseline implementation of the shortcut finding method. You should not modify this method in any way. Instead, you should use it as a point of comparison for your optimized method. -
getShortcutMatrixOptimized()is the method that you will complete for your assignment. Currently, the method simply calls the baseline method. However, you should write a more performant version of the method that employs multithreading as well as memory access optimizations.
-
-
ShortcutTester.javaperforms tests to compare the performance and correctness of yourgetShortcutMatrixOptimized()method. Specifically, the program runs both shortcut computing methods several times on several input sizes and reports (1) the average run-time of the optimized method, (2) the run-time improvement compared to baseline, (3) the number of iterations performed per microsecond (where an iteration consists of single \(\min\) computation in the definition of \(r_{ij}\) above), and (4) whether or not the optimized method produces the same output as the baseline (it should!). -
run-test.shis a shell script that you will use to test your program on the HPC cluster. For now, you should not modify this file.
Hints and Resources
There are two main ways to improve the performance of getShortcutMatrixOptimized () compared to the baseline implementation. The first is to use multithreading. As we saw in Lab 01: Estimating Pi, multithreading can give a sizable speedup for performing operations that can be done parallel. Your optimized method should employ multithreading. Specifically, think about how to break up the task of computing \(D\) into sub-tasks that can be performed in parallel.
We also saw that depending on your own computer hardware, using different numbers of threads will give the best performance. Specifically, your computer cannot perform more threads in parallel than it has (virtual) cores. Since the number of cores varies from computer to computer, it is helpful to know how many processors are available to your program. Thankfully, Java can tell you using the Runtime class. Specifically, the Runtime class provides a method, availableProcessors() which will return the number of processors available on the machine running the program. Using a number of threads roughly equal to this number will tend to give the best performance (assuming you aren’t concurrently running other computationally intensive tasks). You can get the number of available processors by invoking
1
Runtime.getRuntime().availableProcessors();
For relatively small instances (\(n\) up to around 1,000 on my computer), multithreading alone leads to a pretty good performance boost. However, the performance is worse on larger instances. In one run, the baseline program took 2.2s on an instance of size 1024, while an instance of size 2048 took 54.7s. Given the basic algorithm we are applying, we would expect that doubling in instance size increases the number of operations performed by a factor of about \(8 (= 2^3)\). However in this case, doubling the instance size led to a factor 25 increase in run-time. The main reason for this unwelcome slow-down comes down to exactly how modern computers access items stored in their memory through a process of caching. In class, we will discuss caching and how we can improve the performance of our program by making the program behave in a way consistent with how our system expects our program to behave.
Running Your Program on the HPC Cluster
You should do your main development for this (and all other assignments) on your personal computer. You should then use the HPC cluster only for testing and tweaking the performance of your program.
The main documentation for the HPC cluster can be found here: https://hpc.amherst.edu. Note that you need to use the VPN to connect to the website from off campus. The documentation includes instructions for copying files from your computer to the cluster (Files and File Transfer). Note that these instructions refer to romulus, which is an older computing system at the college. To get your files the cluster, you need to replace instance of romulus with hpc.amherst.edu.
From campus, you can log into the HPC cluster from using a terminal/shell on your computer using the command
1
ssh [your-user-name]@hpc.amherst.edu
If everything was successful, you will be greeted with the following screen:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
-------------------------------------------------------------
Amherst College High-Performance Computing Cluster
at MGHPCC in Holyoke, Massachusetts
-------------------------------------------------------------
&&&&#
,&&&/
/&&&/ */// &&&
#&&&&&&&&&&&&&, &&& &&&
,&&&&&&&&&&&&&&&&&&&&&& &&&* &&&
.&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&. ,&& &&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&& &&, &&&
%&&&&&&&&&&&&&&&&&&&&&&&&,&&&&&&&&&&&&& && (&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&& && &&&&&& &&& && &&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&*&&&&&&&&&( *& &&&&#
(&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&& &&&&&&&&%/&&&&&&&.
,&&&&&&&&&&&&&&&&&&&&&&&&&&&&, ,&&&&&&&&&&
&&&&&&&&&&&&&&&&(&&&&&&& &&&&&&&/ (&&&
&&&&&&& #&&&&&/ ,&&&&&& &&&&&&& &&&
&&&&&&& &&&&&&% .&&&&&&, %&&&&&& &&&&%
&&&&&&& &&&&&&& &&&&&&/ &&&&
We welcome our Mammoth Students and Faculty to this new facility.
You can type the command ls to list the files/directories in your home directory. For example, I see the following directories that I created:
1
2
[wrosenbaum@hpc-login1 ~]$ ls
cosc-273 sandbox
You can move to a directory with the cd command. For example, I can move to the directory cosc-273 and see its contents as follows:
1
2
3
[wrosenbaum@hpc-login1 ~]$ cd cosc-273/
[wrosenbaum@hpc-login1 cosc-273]$ ls
activities examples hw labs schedule.md
You can move back to the parent directory of the current directory with cd .., and you can show the path of the current directory with pwd (present working directory).
Once you navigate to the directory storing the program you want to test, you should run the program as specified below. Do not test your program by compiling/running the files directly from the command line! Instead, you should use the provided script run-test.sh and the cluster management software called SLURM. SLURM will allocate the resources necessary to run your test, then will write the output to a specified file. To do this, issue the command sbatch run-test.sh. You will see some output like this:
1
2
[wrosenbaum@hpc-login1 lab02-shortcuts]$ sbatch run-test.sh
Submitted batch job 25360
Then you need to wait until the job completes. (This may take up to 10 minutes if you are testing matrix of size n = 4096.) When the process is complete, the output will be written to a file called shortcutTest.out. You can print the contents of this file to the terminal by using the command cat shortcutTest.out. When the program completes, you should see something like this:
1
2
3
4
5
6
7
8
9
10
11
[wrosenbaum@hpc-login1 lab02-shortcuts]$ cat shortcutTest.out
|------|------------------|-------------|------------------|---------|
| size | avg runtime (ms) | improvement | iteration per us | passed? |
|------|------------------|-------------|------------------|---------|
| 128 | 184 | 0.05 | 11 | yes |
| 256 | 56 | 0.82 | 294 | yes |
| 512 | 19 | 9.22 | 6972 | yes |
| 1024 | 85 | 33.15 | 12497 | yes |
| 2048 | 257 | 88.33 | 33317 | yes |
| 4096 | 1124 | 324.66 | 61095 | yes |
|------|------------------|-------------|------------------|---------|
And that’s it! You’ve compiled and run your program on the HPC cluster! When you’re done, issue the command exit to close your connection with the HPC cluster.
What to Turn In
Be sure to turn in:
SquareMatrix.javawithgetShortcutMatrixOptimized()implemented and commented.- Other
.javafiles defining other classes (you will probably have one implementing theRunnableinterface). - A PDF or plain text document that describes the optimizations you made, and the effect you saw that these optimizations had. Please also mention changes, experiments, or tests you made even if they negatively affected your programs performance. This file need not be more than a couple short paragraphs of text, but it should document the main parts of your program’s development. Your write-up must include the output of
ShortcutTester.javafor executions both on your personal computer as well as the HPC cluster.
Grading
Your programs will be graded on a 10 point scale according to the following criteria:
-
Correctness (2 pts). Your program compiles and completes the task as specified in the program description above. If you program does not pass the correctness tests, you will not receive any points for correctness or performance.
-
Style (1 pt). Code is reasonably well-organized and readable (to a human). Variables, methods, and classes have sensible, descriptive names. Code is well-commented.
-
Performance (4 pts). Code performance is comparable to the instructor’s implementation. Program shows a significant improvement over the baseline when run on the HPC cluster for instances of size 2048 and 4096:
- 0 pts: no siginificant improvement (2048)
- 1 pt: 2-5x improvement (2048)
- 2 pt: 5-10x improvement (2048)
- 3 pt: 10-50x improvement (2048), <200x improvement (4096)
- 4 pt: 50x+ improvement (2048), 200x+ improvement (4096)
-
Documentation (3 pts). Submission includes a
READMEfile indicating (1) the main optimizations made over the baseline implementation, (2) the effect of these optimizations (individually and together), and (3) any other optimizations tested, whether or not they had a positive, negative, or insignificant effect on the program performance. The document should be concise (not more than a couple short paragraphs are necessary), but it should give an indication of the optimizations you tested, what worked, and what didn’t.
Baseline Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public SquareMatrix getShortcutMatrixBaseline () {
int size = matrix.length;
float[][] shortcuts = new float[size][size];
for (int i = 0; i < size; ++i) {
for (int j = 0; j < size; ++j) {
float min = Float.MAX_VALUE;
for (int k = 0; k < size; ++k) {
float x = matrix[i][k];
float y = matrix[k][j];
float z = x + y;
if (z < min) {
min = z;
}
}
shortcuts[i][j] = min;
}
}
return new SquareMatrix(shortcuts);
}