Assignment 08: Tidy Drawings of Trees
nicer tree drawings
For extra credit, submit by Wednesday, May 17 at 5:00 pm
Overview
In class we saw implementations of two methods for drawing binary trees: a greedy method that stacks vertices at the same depth from left to right, and Knuth’s algorithm, which spreads the vertices out horizontally such that each vertex occupies its own column in the figure. In both layout algorithms, vertices are organized in rows, where each row contains all vertices of a given depth. Subject to this constraint, the greedy algorithm ensures that the figure is as narrow as possible. The downside is that the greedy algorithm does not convey information about whether a vertex is the left or right child of its parent. Here is a tree drawn with the greedy procedure:

In contrast, Knuth’s algorithm ensures that if a vertex \(v\) is a left (or right) child of another vertex \(u\), then \(v\) is drawn in a column to the left (or right) of \(u\). Since each vertex occupies its own column, the figure is always \(n\) columns wide for a tree with \(n\) vertices. Here is the same tree as above drawn with Knuth’s algorithm:
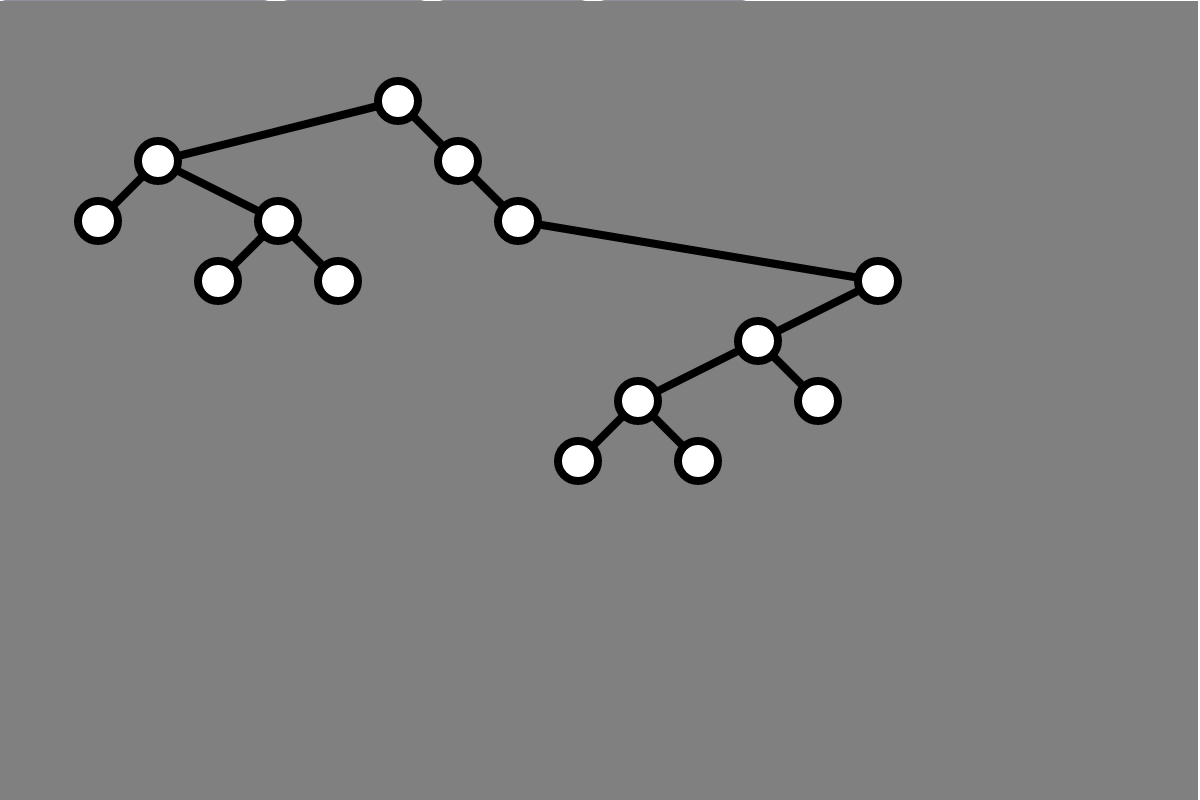
Wetherell and Shannon introduced a procedure that draws a binary tree that maintains the same properties as Knuth’s algorithm, but typically using less horizontal space. Additionally, Wetherell and Shannon’s algorithm ensures that the horizontal position of a parent vertex is always half way between the horizontal position of its children. Here is the resulting figure for the same tree as in the previous two figures:

In this assignment, you will implement Wetherell and Shannon’s Tidy Tree procedure to automatically draw binary trees.
Resources
Wetherell and Shannon’s algorithm is described in Lecture 14 of our course. Additionally, you may refer to their original paper, Tidy Drawings of Trees.
Specification
For your submission, you should implement Wetherell and Shannon’s algorithm in order to visualize any binary tree represented as a BinaryTree object (defined in binary-tree.js):
Specifically, you should complete the method setLayoutTidy in the BinaryTreeViewer class defined in binary-tree.js. The setLayoutTidy method should update the Maps this.xCoords and this.yCoords store the \(x\)- and \(y\)-coordinates of the final position of each vertex in the tree.
You need only submit the file binary-tree.js. Only the setLayoutTidy method should be modified from the original (though you may define additional auxiliary functions called by setLayoutTidy if you’d like).
Assessment
10 points for tidy-tree implementation