Assignment 02: Circular Array Deque Implementation
implementing a double ended queue (deque) with a circular array
Due: Friday, February 18th by 5:00pm
Overview
In class, we saw the List abstract data type (ADT), as well as two
implementations: one using an array data structure, and the other using a linked list. We also saw three related ADTs—Stack, Queue, and
Deque—and how each can be implemented from any List
implementation. In this assignment, you will provide another
implementations of a Deque using a variation of an array called a circular array.
Background
In this assignment, you will provide an implementation of the Deque ADT. The Deque is described in ODS, Section 1.2. See also Chapter 02: Array-based lists.
Circular Arrays/Buffers
An array stores its elements sequentially in a contiguous block at indices \(0, 1, 2, \ldots, n-1\), where \(n\) is the capacity of the array. We often depict arrays as a block of cells storing elements \(0, 1, \ldots, n-1\) from left to right, like this:
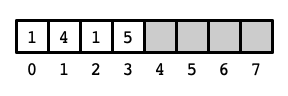
Above is an array of size 8 storing 4 elements with values \(1, 4, 1, 5\), respectively, at indices 0 through 3. It is often helpful, however, to view the elements of the array as if they are arranged in a circle or ring:
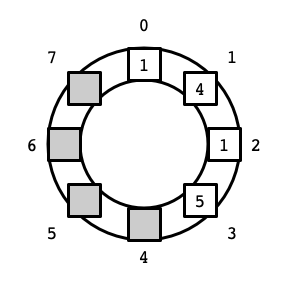
In particular, this view is useful for implementing a deque where elements can be added and removed from both sides of a contiguous block of elements in the array. In our first List implementation using an array, if we wanted to insert an element—say the value 3—before the first element in the list (at index 0), we needed to move all of the other elements to make room for the new element. Viewing the array as a circle makes it evident that there is another way: we can place the new element to the left of 0 at index 7 (assuming this position is not already occupied). Thus, we might store the list of elements \(3, 1, 4, 1, 5\) in the circular array as follows:
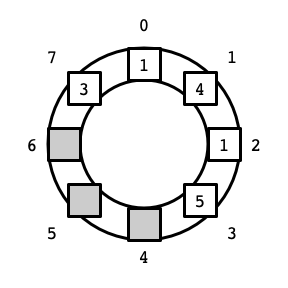
There are two slight complications. The first is that we now need to keep track of two indices: the upper (front) index, and the lower (back) index. In the example above, the lower index is 7 (storing the value 3), and the upper index is 3 (storing the value 5).
The second complication is that when we increase or decrease an index, we might go beyond the bounds of the original array. As the picture above indicates, this can be dealt with in a straightforward manner: if we increase past \(n - 1\) (going over the top of the circle counter-clockwise), we arrive at index \(0\). Symmetrically, decreasing an index from \(0\) brings us to index \(n - 1\). (Arithmetic in which \(0\) is the successor of \(n - 1\) and \(n - 1\) is the predecessor of \(0\) is known as modular arithmetic.) Here is a picture of the contents of the array in its traditional depiction as a block of cells:
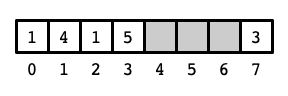
By storing elements in the circular array, elements can be added to and removed from either side of the block storing the contents of a deque without displacing the other elements. In this assignment, you will see that this approach yields significantly better performance of the data structure compared to our original array-based implementation of a deque.
Code
Download this archive containing the following files:
- Interfaces
SimpleDeque.javaSimpleList.java
- Utilities
DequeTester.javaCSVWriter.javaRunTimer.java
- Implementations
ArraySimpleList.javaLinkedSimpleList.javaASLDeque.javaLSLDeque.java
Your Task
For this assignment, you will write and test an implementation of the
Deque ADT: CADeque.java, which implements SimpleDeque using a circular array.
Be sure to test the correctness of your implementation using the provided DequeTester.java. The provided version of DequeTester currently tests the (provided) LSLDeque implementation, so you’ll need to add your implementation to the test. For example, you can test CADeque by setting
1
SimpleDeque<Integer> deque = new CADeque<Integer>();
at the beginning of the main method in DequeTester.java.
You should also write a program that tests the performance of your SimpleDeque implementation. Specifically, it should be able to measure the (average) running times of the SimpleDeque operations for a range of instance sizes (i.e., for various numbers of elements stored in the deque). You should use its output to answer the questions below. For example, you should test the amount of time required for addFirst and addLast for various sizes of deques—say around 50 different values—to get a sense of the trend of how these running times depend on deque size.
Resizing
Your CADeque implementation must dynamically resize its underlying array. That is, if the array is full and a new element is added to the deque, your implementation should create a larger array to store the elements. Good performance can be achieved by doubling the size of the array whenever it is resized.
Testing
The provided tester DequeTester performs some “randomly” chosen operations to check the correctness of your implementation. The parameters of the tester are chosen in the following lines:
1
2
static Random rand = new Random(10);
static final int TEST_SIZE = 1_000;
In this case ther “random seed” is set to 10, and the instance size is set to 1000. The random seed determines which operations are performed, so that if you run the tester with the same parameters multiple time, it will perform exactly the same tests. Different operations will be performed if the random seed and/or TEST_SIZE are set to different values. A correct implementation of a SimpleDeque should pass all tests with any choice of these parameters, while incorrect implementations may pass the tests for some and fail tests for others. Your submission will be tested with different parameters than those above.
Questions
Please answer the following questions about your programs. Be sure to support claims with evidence (e.g., running times).
-
Consider the
addFirstandaddLastmethods for yourCADeque. How does the running time of these methods depend of the size of the deque? -
How do the running times of
addFirstandaddLastcompare between your implementations and the provided list-based implementations,ASLDequeandLSLDeque?
What to Submit
You should submit:
CADeque.javacontaining yourSimpleDequeimplementation using a circular array,responses.pdfcontaining your responses to the questions above.- any code you used to generate
responses.pdf
Evaluation
Your submission will receive a score out of 10 points, broken down as follows:
- 5 points each for
DLLDeque.java- code compiles, runs, and passes all tests in
SimpleDequeTester.java - code correctly implements a circular array
- code is well organized and documented with comments
- code compiles, runs, and passes all tests in
- 5 points for responses to the questions above