Lecture 27 Ticket

At the end of Lecture 26, we discussed a generalization of the shortest paths problem to directed graphs. In a directed graph, each edge has an associated direction. Pictorially, we can represent directed edges as an arrows between vertices:

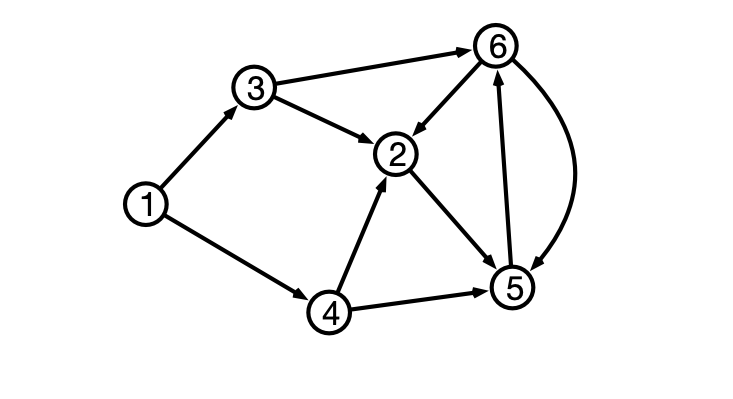
In the figure above, there is a directed edge from \(1\) to \(3\), but not from \(3\) to \(1\). We call this edge an outgoing edge for vertex \(1\) and an incoming edge for vertex \(3\). We denote a directed edge from \(u\) to \(v\) by \((u, v)\). Here, the order of vertices is important: \((u, v) \neq (v, u)\) as the former indicates an edge from \(u\) to \(v\), while the latter indicates an edge from \(v\) to \(u\). A directed graph is allowed to contain both of these edges. The example above contains both the edges \((5, 6)\) and \((6, 5)\).

Directed graphs can be represented by adjacency lists, where each vertex’s adjacency list contains only its outgoing neightbors. For example, the graph depicted above can be represented by the following adjacency lists:

In directed graphs, we can consider directed paths. As before, a path \(P\) is a sequence of the form \(v_0 e_1 v_1 e_2 v_2 \cdots v_{k-1} e_k v_k\) where each \(v_i\) is a vertex, and \(e_i\) and edge. For a directed path, \(e_i = (v_{i-1}, v_i)\) is a directed edge from \(v_{i-1}\) to \(v_i\). In the example above, there are directed paths from \(1\) to \(6\) (e.g., \(1, 3, 6\)), but there is no directed path from \(6\) to \(1\). We can also consider weighted directed graphs where each (directed) edge has an associated weight. For weighted directed graphs, it can be the case that the graph contains directed edges \((u, v)\) and \((v, u)\) with different weights: \(w(u, v) \neq w(v, u)\). As with undirected graphs, the weight or length of a directed path is defined to be the sum of the weights of the (directed) edges of the graph.

The two algorithms for single source shortest paths–breadth-first search (BFS) and Dijkstra’s algorithm–both work just as well for directed graphs as undirected graphs, given the adjacency list representation. (You should convince yourself this is true.) However, BFS works only for unweighted graphs, and Dijkstra’s algorithm is only guaranteed to work when all edge weights are non-negative. In this exercise, you will show that things are more subtle when edge weights are allowed to be negative.

1. Give an example of a weighted directed graph with one edge with negative weight and at most four vertices such that Dijkstra’s algorithm produces incorrect distances.

2. Give an example of a graph with both positive and negative edge weights such that there is a directed path from a vertex \(u\) to another vertex \(v\), but there is no shortest (directed) path from \(u\) to \(v\).