Lecture 04 Ticket Solution

Consider the following method that on input a positive integer \(n\) sums the odd numbers from \(1\) to \(2 n - 1\):

1
2
3
4
5
6
  Sum(n):
    total <- 0
    for k = 1 up to n do
      total <- total + 2 * k - 1
    endfor
    return total

Observe that for \(n = 1, 2, 3, 4\), \(\mathrm{Sum}(n)\) returns the values \(1, 4, 9, 16\). In each case, the value returned by \(\mathrm{Sum}(n)\) is \(n^2\). Use induction to argue that this formula always holds: for every positive integer \(n\), the value returned by \(\mathrm{Sum}(n)\) is \(n^2\).

Solution

Consider the for loop in lines 3-5. We claim that for each iteration \(k\), the value of \(\total\) at the end of iteration \(k\) is \(k^2\). We prove this claim by induction.

Base case. For the base case, \(k = 1\), note that before the first iteration of the loop, we have \(\total = 0\) (from line 2). Therefore, in iteration \(k = 1\), at line line 4 \(\total\) gets assigned the value \(0 + 2 * (1) - 1 = 1 = k^2\). Therefore the claim holds for \(k = 1\).

Induction step. Now suppose the claim holds for some value of \(k\). That is, after iteration \(k\), we have \(\total = k^2\). Consider iteration \(k + 1\). Then in line 4, \(\total\) is assigned the value

Thus, after iteration \(k+1\), we have \(\total = (k+1)^2\), so the claim holds.

Since both the base case and inductive step hold, the claim holds for all iterations \(k\) by induction. Finally, observe that loop terminates after iteration \(n\), so the value of \(\total\) returned by \(\mathrm{Sum}(n)\) is \(n^2\).

A Note on the Formula

Given a positive integer \(n\), we can interpret the value \(n^2\) geometrically as the area of a square with side length \(n\). For example, the square figure below (left) has side length 8, and is (evidently) comprised of \(64 = 8^2\) unit squares.

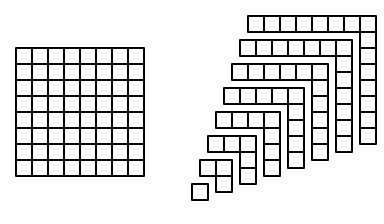
We can decompose the \(8 \times 8\) square grid into \(8\) “L”-shapes as on the figure on the right. The “L”s have width and height \(1, 2, 3, \ldots, 8\), and their areas are \(1, 3, 5,\ldots 15\). Since the figure on the right is just a partition of the figure on the left, they have the same area. Thus, the figures give a geometric interpretation to the formula