Final Exam Study Guide
your guide for the final exam for COSC 311: Algorithms, fall 2022 edition
Overview
The final exam for Algorithms will be held in SCCE E110 on Friday, December 16th from 9:00 am to 12:00 pm.
The exam will be cumulative, though emphasis will be given to topics that have not appeared on previous exams. Below you will find a complete list of topics that are fair game for the exam.
The format of the exam is closed book/closed note and any form of collaboration is strictly prohibited. You will be provided with a “cheat sheet” containing (at least) the following information:
- statement of the master theorem
- definition of the class NP and verifier
- a list of NP complete problems
The exam consists of approximately 8 questions. Most questions will be of the following types:
-
Simulate an algorithm examined in class by hand to solve a given instance. You should be able to do this for the “named” algorithms in class, e.g., Dijkstra’s algorithm, Prim’s algorithm, the Ford-Fulkerson algorithm, etc.
-
Devise an algorithm for a new problem using a particular paradigm (e.g., greedy, divide and conquer, dynamic programming). It will be helpful to be familiar with the examples of problems we encountered in lecture and the homework assignments.
-
Derive a reduction between a new problem and some problem we examined in class (e.g., reduction to maximum flow or proving NP completeness).
Below is a list of 6 questions that are representative of the types of queestions you might expect to see on the exam.
Topics
Analysis of Algorithms
Lectures 1–3
- big O notation
- induction and loop invariants
Sorting
- elemenatry algorithms (lectures 1–3)
- selection sort
- insertion sort
- bubble sort
- divide and conquer algorithms (lectures 4–9)
- merge sort
- quicksort
- radix sort
- comparison based lower bound for sorting (lecture 8)
Divide and Conquer Algorithms
- Karatsuba multiplication (lecture 10)
- binary search, maximization (lecture 12)
- master theorem for analysis (lectures 11–12)
Greedy Algorithms
- Eulerian circuit/brideges of Koenigsberg (lecture 13)
- breadth-first search (BFS) and unweighted single source shortest paths (SSSP) (lectures 14–15)
- Dijkstra’s algorithm (lectures 16–17)
- minimum spanning trees (MST) (lectures 17-20)
- Prim’s algorithm
- Kruskal’s algorithm
- interval scheduling (lecture 21)
Dynamic Programming
- profit maximization (lecture 22)
- weighted interval scheduling (lecture 23)
- weighted knapsack (lecture 24)
- sequence alignment (lectures 25–26)
- Bellman-Ford (lectures 27–28)
Network Flow
- maximum flow problem definition (lecture 28)
- Ford-Fulkerson algorithm (lecture 29)
- max-flow/min-cut (lecture 30)
Reductions and NP
- maximum bipartite matching reduction to MaxFlow (lecture 32)
- polynomial time reductions (lecture 33)
- P and NP (lecture 34)
- NP completeness (lecture 35)
- NP complete problems and reductions (lecture 36)
Example Problems
Problem 1 (graph distance and spanning trees). Consider the following weighted graph:
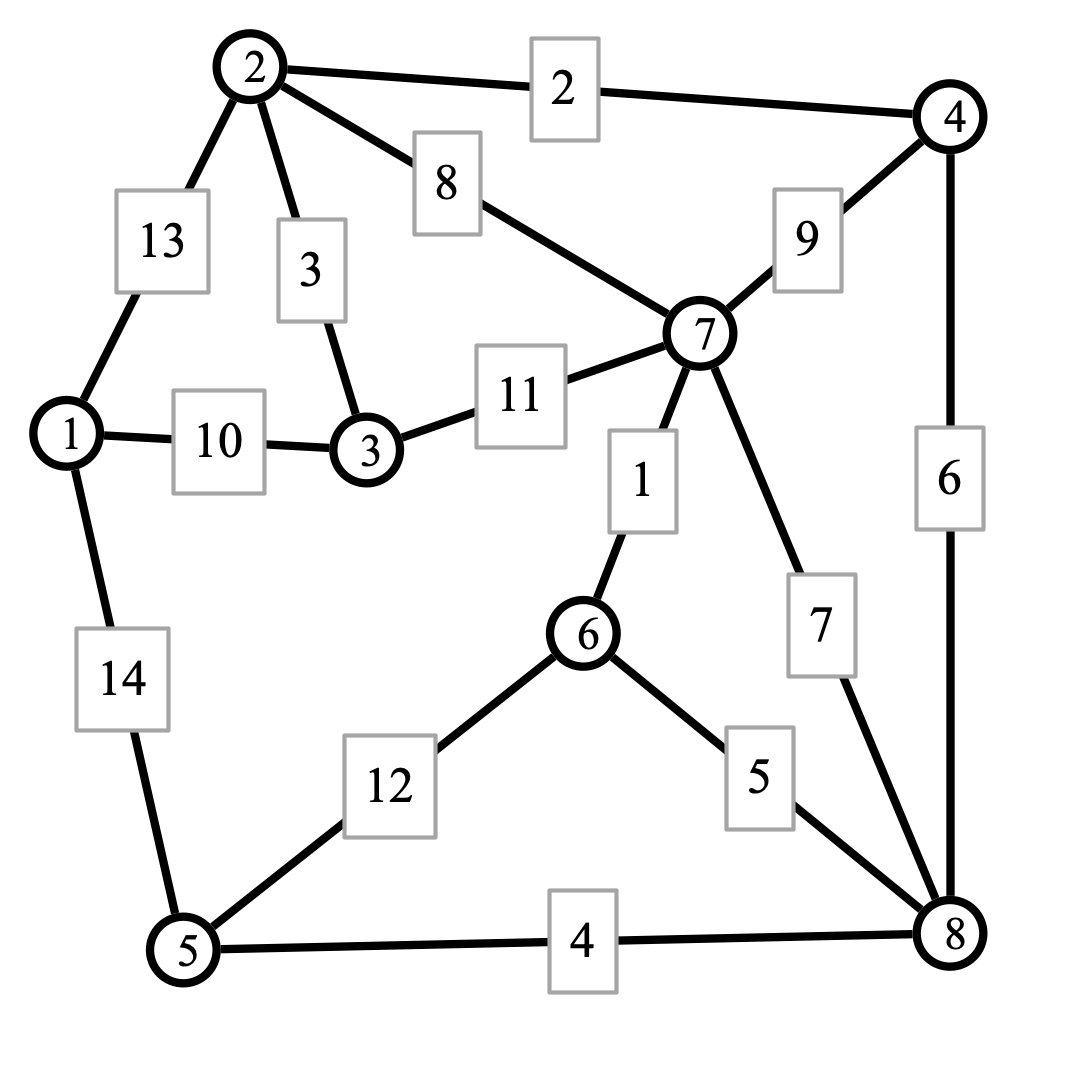
-
Apply Dijkstra’s algorithm to find the distance of every other vertex from vertex 1. Also indicate the shortest paths from 1 to each other vertex. (Note that the shortest paths form a spanning tree.)
-
Apply your favorite algorithm to find a minimum spanning tree (MST) for the graph.
Problem 2 (counting inversions). Suppose \(a\) is an array of integers of size \(n\). Recall that two indices \(i, j\) are an inversion if \(i < j\) and \(a[i] > a[j]\). It is straightforward to count the total number of inversions in an array in time \(O(n^2)\) by iterating over all pairs of indices \((i, j)\) and checking if each is an inversion.
Suppose you are given a method \(\SplitInversions(a, r, s, t)\) that, given an array \(a\) and indices \(r, s, t\) satisfying \(r < s < t\), computes the number of inversions \((i, j)\) in \(a\) with \(r \leq i < s\) and \(s \leq j < t\), and whose running time is \(O(t - r)\). Design a divide and conquer algorithm that uses \(\SplitInversions\) as a subroutine to compute the number of inversions in \(a\). Use the master theorem to compute the running time of your procedure (which should be substantially faster than \(O(n^2)\).
Challenge. Modify MergeSort so that it outputs the number of inversions in the array it sorts. In particular, your “merge” subroutine should output the result of a corresponding call to \(\SplitInversions\).
Problem 3 (longest common subsequences). Suppose \(a\) and \(b\) are arrays of length \(n\) and \(m\), respectively. We say that \(a\) and \(b\) have a common subsequence of length \(k\) if there are indices \(1 \leq i_1 < i_2 < \cdots < i_k \leq n\) and \(1 \leq j_1 < j_2 < \cdots < j_k \leq m\) such that \(a[i_1] = b[j_1], a[i_2] = b[j_2], \ldots, a[i_k] = b[j_k]\). For example, if \(a = [A, L, G, O, R, I, T, H, M]\) and \(b = [A, M, H, E, R, S, T]\), then \(A, R, T\) is a common subsequence of \(a\) and \(b\) of length 3.
Use dynamic programming to devise an algorithm that computes the length of the longest common subsequence of two arrays in time \(O(n m)\).
Hint. Suppose \(a\) and \(b\) are given. For \(i \leq n\) and \(j \leq m\), let \(\lcs(i, j)\) be the length of the longest common subsequence of \(a[1..i]\) and \(b[1..j]\). How does \(\lcs(i, j)\) relate to other values of \(\lcs\)? What if \(a[i] = b[j]\)? Or if \(a[i] \neq b[j]\)?
Problem 4 (Ford-Fulkerson computation). Consider the following directed weighted graph \(G\) with source \(s\) and sink \(t\):
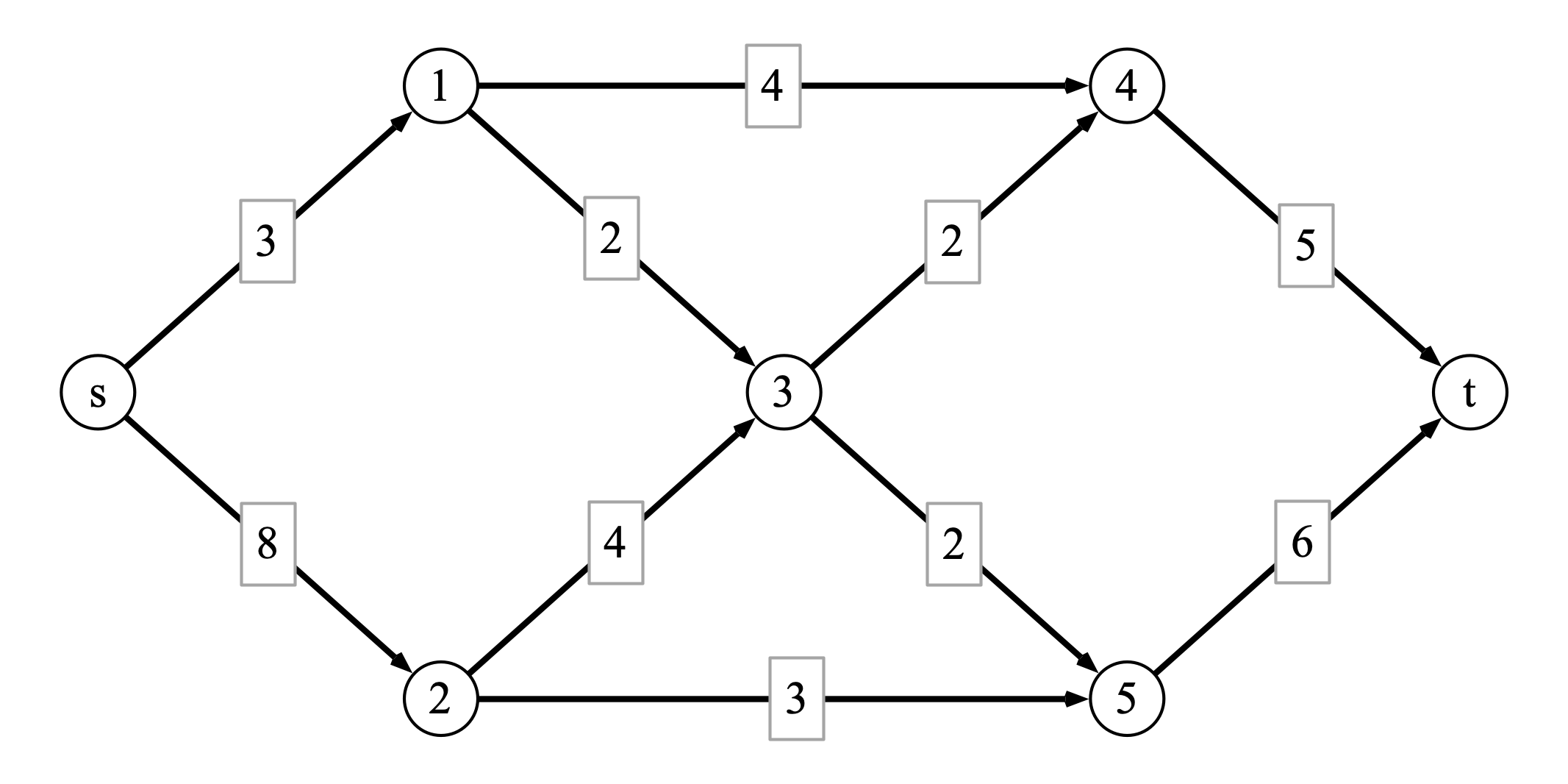
At some intermediate step of executing the Ford-Fulkerson algorithm, you find the flow \(f\) defined as follows:

The following questions refer to the process of completing an execution of Ford-Fulkerson on the graph.
- What is the value of the flow \(f\) defined above?
- Draw the residual graph \(G_f\) resulting from the flow \(f\) on \(G\).
- Find an augmenting path for the graph \(G_f\).
- Write the flow resulting from routing additional flow through the augmenting path you found in step 3.
- Argue that the flow you found in part 4 is a maximum flow.
Problem 5 (MaxFlow reduction). After college, three friends, Alice, Bob, and Carol, decided to move to the city and live together as roommates. In order to save time and money, they decide that every night except Saturdays, one of them will cook for everyone in the apartment. In order to do things equitably, they would like to come up with a schedule in which each person cooks dinner two nights a week. The roommates lead busy lives, however, and they are not available to cook every night: Alice is only able to cook on Mondays, Wednesdays, and Fridays; Bob is only availble on Tuesdays, Thursdays, and Fridays; Carol can only cook on Wednesdays, Fridays, and Sundays.
- Draw a bipartite graph that indicates the three roommates’ availabilities to cook.
- Given the graph of part 1, how could you determine if there is a cooking schedule such that each roommate cooks two nights a week, and someon cooks every night (except Saturdays).
- How could you transform the graph from 1 into an instance of MaxFlow such that finding a maximum flow will either reveal a cooking schedule as in part (2) or indicate that no such schedule exists?
Problem 6 (NP completeness). In a film class at Cook-Levin University, the \(m\) students are asked to list a few of their favorite movies for a list of “The \(n\) Greatest Movies of All Time,” (for some value of \(n\)). A semester lasts \(k\) weeks, and the class can only screen a single film each week. Your task is to determine whether or not it is possible to choose a selection of \(k\) movies such that at least one movie from each student’s list is screened at some point in the semester. Show that your task is NP-complete.