Will Rosenbaum | Homework 05

Download this assignment in pdf format or .tex source.

\[\def\lis{ {\mathrm{lis}} }\]

Exercise 1 (scriptio continua). In modern writing in most Western languages, it is customary to distinguish words by writing spaces between words. Many ancient texts, however, are written in scriptio continua (for “continuous script”): the text appears as a continuous string of characters without punctuation or spaces between words. Thus (an English translation of) the opening to Homer’s Iliad might appear as

  singgoddessoftheangerofachillessonofpeleus
  accursedwhichbroughtcountlesspainsuponthea
  chaeanshurledtohadesmanystrongsoulsofheroe
  sservedthemupascarrionforthedogsandalltheb
  irdsthewillofzeusbeingfulfilledsincetheson
  ofatreuslordofmenandgodlikeachillesfirstfe
  udedandquarreled

For those unaccustomed to reading scriptio continua, this style of writing might be troublesome to read.

For this problem, assume you are given a text written in scriptio continua, represented as an array $a$ of $n$ characters. Your goal is to determine whether or not the text can be segmented into a sequence of words. To this end, you are given access to a dictionary that will tell you if a given sequences of letters form a word. The dictionary can be accessed via a method called isWord(a, i, j) which returns true if the letters $a[i..j]$ form a word, and false otherwise.

Write a dynamic programming algorithm that, given an array $a$ of size $n$, returns true if $a$ can be segmented into words and false otherwise. Assuming each call to isWord can be computed in time $O(1)$, the running time of your procedure should be no more than $O(n^2)$.
(Challenge). Modify your procedure from part 1 to return the number of ways in which $a$ can be segmented into words. Argue that for some strings $a$, the number of possible segmentations is $2^{\Omega(n)}$.

Exercise 2. Imagine that you have decided to open a small business, and your grand entrepreneurial idea is to take steel rods of length $n$, cut up the rods into smaller pieces, and sell the pieces. You know something about the market for steel rods, so you know that you can sell a piece of length $i$ for price $p_i$, where $p_i \leq p_j$ if $i < j$ (a longer piece is worth at least as much as a shorter piece). Your goal is to figure out how best to cut up the length-$n$ rods in order to make the highest profit. The rod cutting problem is defined as follows:

Input: a length $n$, and, for all (positive, integer) $i \leq n$, a price $p_i$ for which you can sell a rod of length $i$. You may assume that these values are stored as an array $p$ of length $n$ so that $p_i = p[i]$.
Output: a decomposition of the length-$n$ rod into shorter pieces so that the total price of all of the shorter pieces is maximized. That is, you should output an array $d$ of length $n$, where $d[i]$ is the number of pieces of length $i$ in your decomposition.

Note that the decomposition may contain multiple pieces of the same size.

Give a recursive solution to the rod cutting problem. Your recursive function price(n, p) should determine the best sale price for a rod of length $n$, which may be cut up in any possible way.
Here’s an example for a rod of length 5:
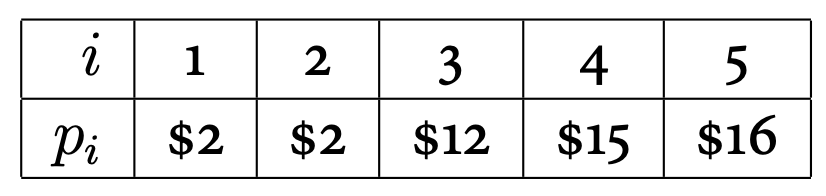
- On this example, trace enough of your recursive algorithm to show that there are repeated subproblems.
- Estimate the (worst-case) runtime of your recursive algorithm in terms of $n$, the length of the original rod.
Now, design a bottom-up dynamic programming algorithm based on your recursive solution.
- Your algorithm should fill in a table. Describe that table: how many columns, how many rows, what is in the cells?
- Describe your algorithm.
- Show what happens when you run your algorithm on the input above (i.e., what solution does your algorithm find, and how does it go about finding this solution?)
In terms of $n$ (the length of the original rod), what is the runtime of your algorithm?
Explain how you know that your algorithm produces an optimal solution.

Exercise 3 (Challenge). Given a sequence of numbers $a_1, a_2, a_3, \ldots, a_n$, we say that a subseqeunce $a_{i_1}, a_{i_2}, \cdots, a_{i_k}$ is an increasing subsequence of length $k$ if $a_{i_1} < a_{i_2} < \cdots < a_{i_k}$ with $i_1 < i_2 < \cdots < i_k$. For example, the sequence $8, 2, 5, 4, 3, 9, 6, 1, 7$ contains the increasing subsequence of length 4, $2, 4, 6, 7$. Given a sequence $a = (a_1, a_2, \ldots, a_n)$, let $\lis(a)$ denote the length of the longest increasing subsequence in $a$. The value $\lis(a)$ can be viewed as a measure of how sorted $a$ is: if $\lis(a) = n$, then $a$ is sorted, while $\lis(a) = 1$ only if $a$ is descending.

In this exercise, you will devise an algorithm that finds the longest increasing subsequence of a sequence $a$. Specifically, your algorithm will read the sequence $a$ only once in order and produce its solution.

Suppose the values from $a[1..i-1]$ (i.e., $a_1, a_2, \ldots, a_{i-1}$) have been read, and you are given an array $\min$ with the following semanics: If $\min[j] = b$ then
1. $a[1..i-1]$ contains an increasing sequence of length $j$ ending with the value $b$, and
2. $b$ is the smallest value for which $a[1..i-1]$ contains an increasing sequence of length $j$ terminating terminating at $b$.
If you are given the next value of the sequence, $a[i]$, how can you update the array $\min$ so that conditions 1 and 2 above hold for $a[1..i]$?
Argue that your update described above can be performed in $O(\log k)$ time if $\lis(a) = k$. (Hint: What can you say about the values of $\min[1], \min[2], \ldots$? How large can the array $\min$ be?)
Using your solutions to parts 1 and 2, devise a procedure that computes $\lis(a)$ in time $O(n \log n)$.
(Uber challenge.) Suppose $n \geq (r - 1) (s - 1) + 1$ for some values of $r, s \geq 1$. By analyzing your algorithm from part 3, argue that every sequence of length $n$ has either an increasing subsequence of length at least $r$ or a decreasing subsequence of length at least $s$. This result is known as the Erdős–Szekeres theorem. (Hint: The size of $\min$ is $\lis(a)$, and $\min$ is updated $n$ times. If a particular index $\min[i]$ is updated $\ell$ times, what can you say about the sequence of update values?)