Homework 2
You can download a PDF of this assignment here.
Instructions
You may work in groups of up to 4 and submit a single assignment for the group. For computational problems, please show your work; for conceptual questions, please explain your reasoning. Solutions may be neatly hand-written and scanned or typeset. Please submit your solution to Moodle in PDF format.
Due: Friday, March 19, 23:59 AoE
Exercises
Exercise 1. Consider the following Bouncer object:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Bouncer {
public static final int DOWN = 0;
public static final int RIGHT = 1;
public static final int STOP = 2;
private boolean goRight = false;
private int last = -1;
int visit () {
int i = ThreadID.get();
last = i;
if (goRight)
return RIGHT;
goRight = true;
if (last == i)
return STOP;
else
return DOWN;
}
}
Suppose \(n\) threads call the visit() method. Argue that the following hold:
- At most one thread gets the value
STOP. - At most \(n - 1\) threads get the value
DOWN. - At most \(n - 1\) threads get the value
RIGHT.
Exercise 2. So far in this course, we have assumed that all threads have IDs that are reasonably small numbers. In Java, however, thread IDs can be arbitrary long values (see getId() documentation). In this exercise, we will see how to use Bouncer objects as above to create unique IDs that are reasonably small compared to the number of threads.
Consider a 2D triangular array of Bouncer objects arranged as follows:
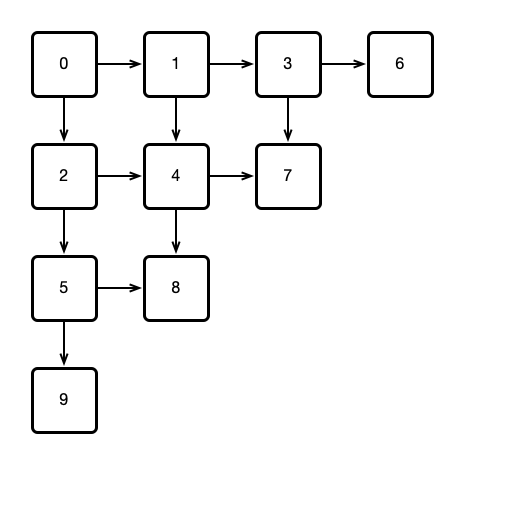
Suppose each thread performs the following procedure: All threads start by calling visit() on Bouncer 0. Whenever a thread visits a Bouncer, if the Bouncer returns STOP, the thread adopts the number of the Bouncer as its ID. If DOWN is returned, the thread then visits the Bouncer below; if RIGHT is returned, the thread visits the Bouncer to the right.
- Show that for a sufficiently large array of
Bouncers, every thread will eventuallySTOPat someBouncer, thereby adopting its ID. - If the number \(n\) of threads is known in advance, how many
Bouncers are required to ensure that all threads adopt an ID?
Hint. For each thread, consider its location before each call to visit(). That is, in the first step, all threads call visit at Bouncer 0. In the second step, some threads might visit Bouncer 1, and others visit Bouncer 2, while at most one thread STOPs at Bouncer 0. At a given step, call a Bouncer occupied if a thread is STOPped at it, or at least one thread will call visit() on it. For example, only the first Bouncer is occupied in step 1, while Bouncers 0, 1, and 2 could be occupied in step 2. Consider the number of occupied Bouncers each step. Can this number decrease? Could this number ever be greater than \(n\)? If the number of occupied Bouncers is strictly less than \(n\) (i.e., multiple threads are visiting some Bouncer), is it possible that the same number of Bouncers will be occupied in the next step?
Exercise 3. Consider the following histories of executions of read/write registers (variable), r and s. Please explain your answers to the following questions.
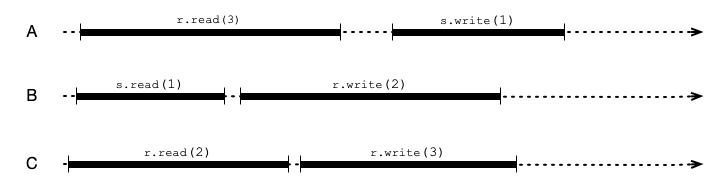
-
Restricting attention only to register
r, is the execution sequentially consistent? Linearizable? -
Restricting attention only to register
s, is the execution sequentially consistent? Linearizable? -
Is the entire execution (including both registers) sequentially consistent? Linearizable?