How Slow is Recursive Fibonacci?
Examining the efficiency of a recursive method.
In lecture, we saw that the recursive solution to computing the Fibonacci numbers is much slower than the iterative version. How much slower? These were the results comparing the amount of time the two programs required for a few reasonably large values:
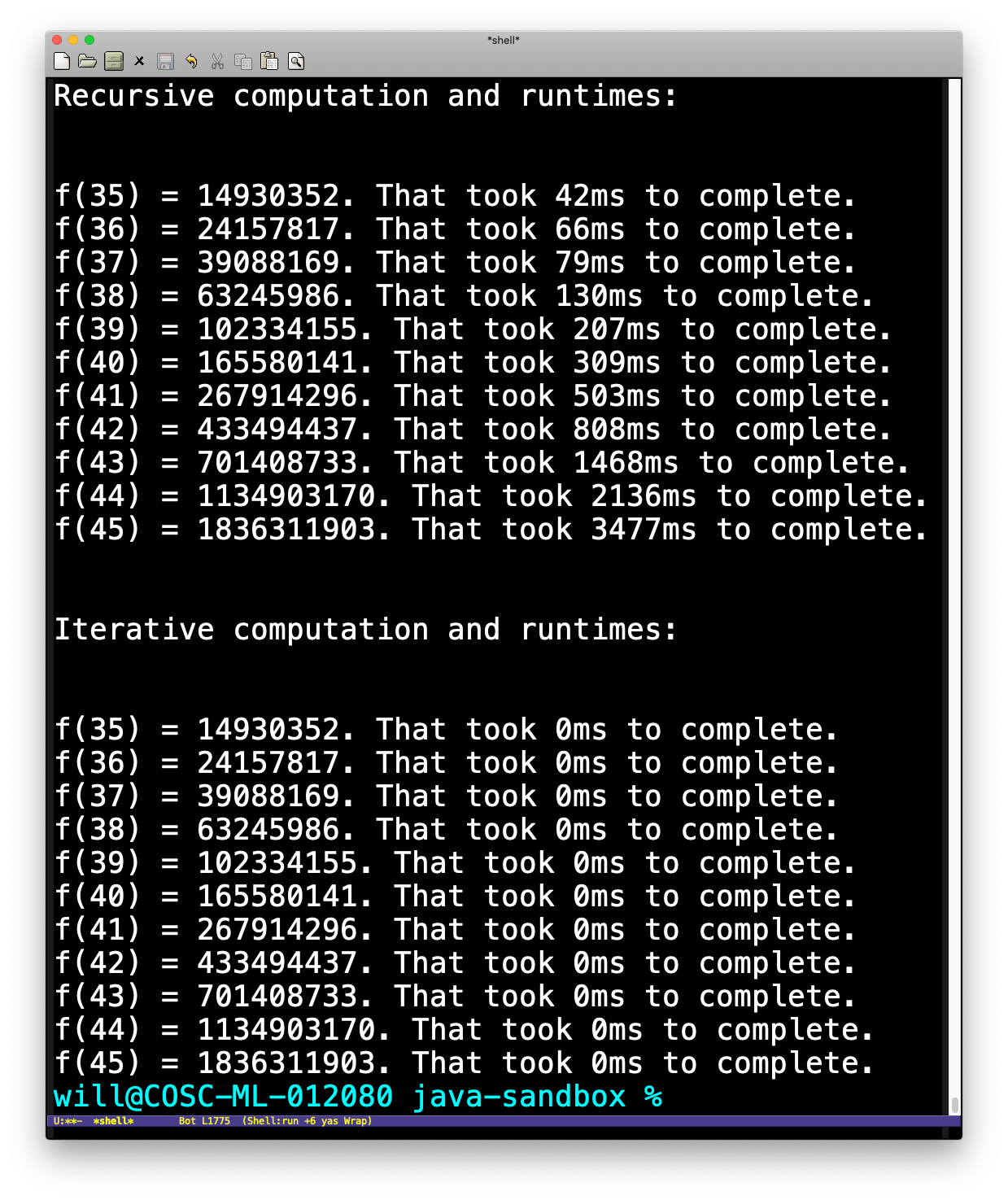
For example, computing f(45) recursively required almost 3 1/2 seconds, while the iterative solution finished in less that 1 ms. So the recursive solution is (at least) 3,500 times slower than the iterative solution! But why?
Recursive Calls
To understand why the recursive fibonacci method is so slow, it helps to understand how many “recursive calls” the method makes. That is, if we execute fibonacci(n), how many times does fibonacci(<something>) actually get called? Here is the code for reference:
1
2
3
4
5
private static int fibonacci (int n) {
if (n <= 2) return 1;
return fibonacci(n-1) + fibonacci(n-2);
}
For small values of n, we can compute the number of recursive calls directly. For n = 1 and n = 2, the function hits return 1, without any recursive calls to fibonacci(...). Now fibonacci(3) executes
1
return fibonacci(2) + fibonacci(1);
so there are 2 recursive calls made. What about fibonacci(4)? In this case, we execute
1
return fibonacci(3) + fibonacci(2);
Thus there are 2 recursive calls again. But fibonacci(3) itself makes 2 recursive calls (by the above), while fibonacci(2) makes none. So the total number of calls to fibonacci(<something>) by fibonacci(4) is 2 + 2 + 0 = 4.
Note that we are already seeing some repeated work: fibonacci(4) calls fibonacci(3) and fibonacci(2), but fibonacci(3) also calls fibonacci(2). So the code is computing the same thing twice, and having to waste time performing each repeated call!
The following figure shows the so-called recursion tree corresponding to an execution of fibonacci(6):
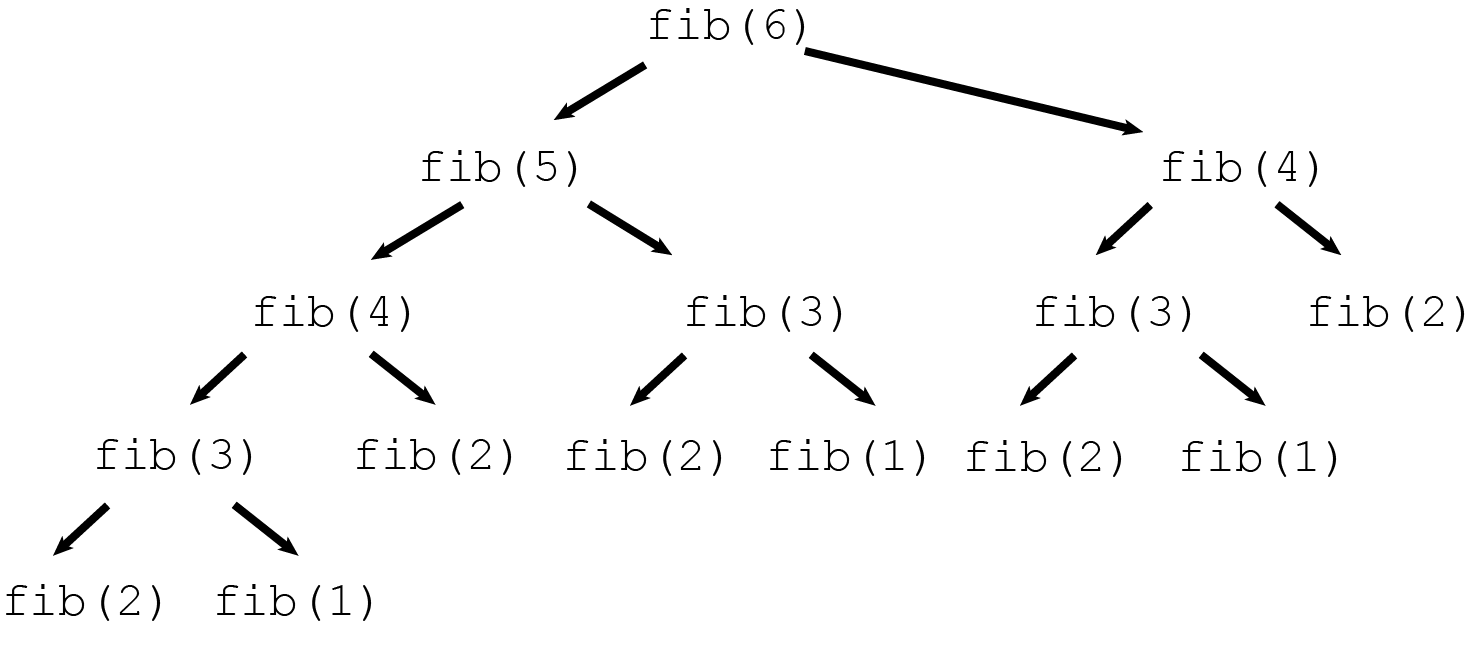
This tree illustrates which calls to fibonacci (fib in the image) make recursive calls. Note that fib(4) gets called twice, fib(3) three times, fib(2) 5 times, and fib(1) 3 times. That is a lot of wasted effort!
The diagram above is what computer scientists and mathematicians call a tree. The bottom-most nodes (labeled fib(2) and fib(1)) are the leaves. These correspond to the “base cases” in the recursion, as these cases do not make recursive calls to fib. The root is the top-most node, labeled fib(6) in our picture. Weirdly, mathematicians and computer scientists draw “trees” with “leaves” at the bottom and a “root” on top, which is the opposite of how an actual tree outside grows. Go figure.
Depth of recursion
The depth of a recursion tree is the is the length of the longest path from the root to any leaf. For example, in the image above, the longest path from the root (labeled fib(6)) to any leaf is the path following the recursive calls fib(5) , fib(4), fib(3), fib(2) (or fib(1)). This path has length 4 (there are 4 recursive calls along both the paths to fib(2) and fib(1) the path), so the depth of recursion for this computation of fib(6) is 4.
Computing the number of recursive calls
In general (for n > 3), a call to fibonacci(n) makes 2 recursive calls to fibonacci(n-1) and fibonacci(n-2). These recursive calls in turn make more recursive calls. How many?
Well… we can compute it! We can write a method numberOfCalls(int n) that counts the number of recursive calls fibonacci(n) makes. Note that we should have
numberOfCalls(1)returns 0numberOfCalls(2)returns 0
On the other hand, for n > 2, fibonacci(n) makes recursive calls to fibonacci(n-1) and fibonacci(n-2). So numberOfCalls(n) should return 2 + \numberOfCalls(n-1) + \numberOfCalls(n-2). So we are led to another recursive function definition:
1
2
3
4
5
6
7
private static int numberOfCalls (int n) {
if (n == 1 || n == 2) {
return 0;
}
return 2 + numberOfCalls(n - 1) + numberOfCalls(n - 2);
}
Here’s the the output for the first few values of n:
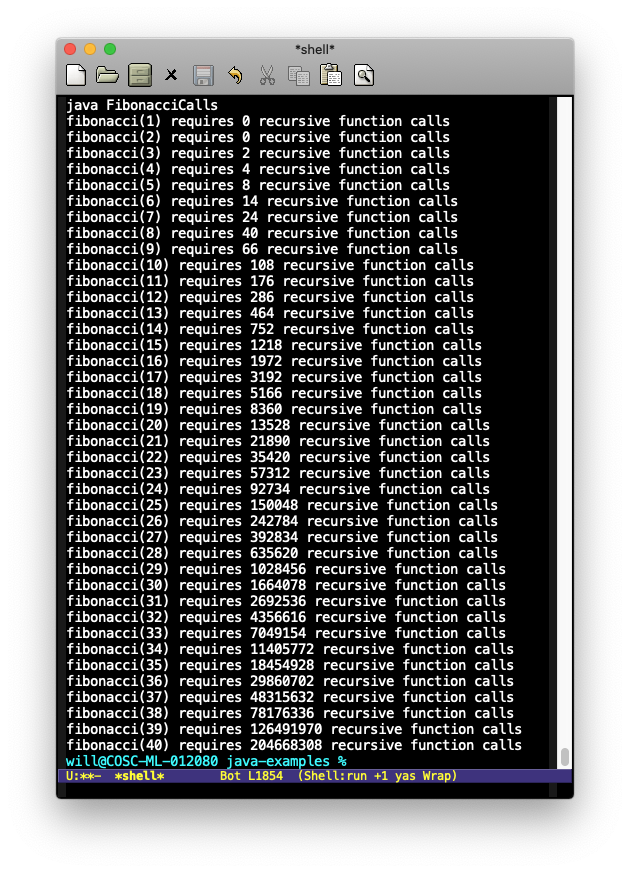
Note the pattern: the number of recursive calls almost doubles each time n increases by one. So computing fibonacci(11) this way requires almost twice as much work as fibonacci(10), and so on. Obviously, this is wasteful!
A more efficient thing to do would be store each value of fibonacci(n) when it is computed, say, in an array. Instead of re-computing each value from scratch, the program could then look up a value to see if it has been computed before. If so, it can simply fetch the stored value rather than making a new recursive call.
Question
How many recursive calls does numberOfCalls(n) make?