Lab 05: Monte Carlo
using randomness to estimate areas
Due: Friday, April 16, 23:59 AoE.
Background
Monte Carlo simulation is a tool that employs randomness to estimate quantities that are difficult—if not imppossible—to compute precisely. In this lab, you will use a Monte Carlo simulation to estimate the area of shapes composed of overlapping disks. We call such a shape a blob. Here, we have a blob consisting of a single disk:
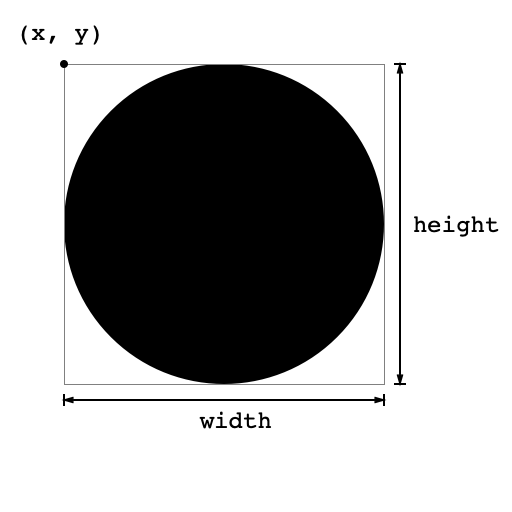
Depicted above is the blob together with its bounding box: the smallest axis-aligned rectangle that contains the blob. The bounding box is specified by the \((x, y)\)-coordinates of its upper left conrner, its width, and its height.
In the case of a blob consisting of a single disk, it is easy to compute the area of the blob using the well-known formula for the area of a disk \(A = \pi r^2\). However, what if we have a more complicated blob, like the one picture below?

This blob consists of 5 disks. I am not aware of any nice formula for computing the area of such a figure, so in order to estimate its area, we will use a Monte Carlo simulation. The idea is as follows. If we generate a random point inside the bounding box—say, by throwing a dart at the figure—the probability that the point hits the blob is the ratio of the area of the blob to the area of the bounding box. Symbolically:
\[p = \mathrm{Pr}[\text{point hits blob}] = \frac{A_{\mathrm{blob}}}{A_{\mathrm{box}}}.\]Here \(A_{\mathrm{blob}}\) is the area of the blob, and \(A_{\mathrm{box}} = \mathrm{width} \times \mathrm{height}\) is the area of the bounding box. Solving for \(A_{\mathrm{blob}}\)—our quantity of interest—we obtain
\[\begin{equation} A_{\mathrm{blob}} = p \cdot A_{\mathrm{box}}. \end{equation}\]Thus, in order to estimate \(A_{\mathrm{blob}}\), we need only estimate \(p\), the probability that that a randomly chosen point in the bounding box hits the blob. We can obtain an estimate of \(p\) by repeatedly choosing random sample points, and taking as our estimate the proportion of samples that land in the blob. Symbolically:
\[\begin{equation} p \approx \frac{\text{# samples hitting blob}}{\text{# total samples}}. \end{equation}\]Putting together, equations (1) and (2), we get
\[\begin{equation} A_{\mathrm{blob}} \approx \frac{\text{# samples hitting blob}}{\text{# total samples}} \cdot A_{\mathrm{box}}. \end{equation}\]For example, suppose we generate 25 random points in the bounding box of previously depicted blob:

A total of 17 points are contained in the blob. If the bounding box has a width and height of \(4 \mbox{cm}\), hence an area of \(4 \mbox{cm}^2\), our estimate of the area of the blob is
\[A_{\mathrm{blob}} \approx \frac{17}{25} \cdot 16 = 10.88 \mbox{cm}^2.\]We may need to produce a lot of samples in order to estimate the area of a blob accurately, but thankfully computers are good at doing a lot of computations quickly!
Your Task
Your task is to implement a Monte Carlo simulation to estimate the area of a blob. To get started, download the program files below:
MonteCarlo.zip contains four program files:
AbstractShape.java: an abstract class representing a shape.Circle.java: a subclass ofAbstractShapethat represents a disk.Blob.java: a class representing a blob consisting of one or moreAbstractShapes.AreaTester.java: a program to start testing your Monte Carlo estimation program.
You will implement the main methods in Blob.java. The Blob is represented as ArrayList<AbstractShape> shapes, where the individual elements of shapes are the constituent shapes making up the Blob. Specifically, you should implement the following methods:
double getXMin()returns the minimumxcoordinate of the blob—i.e, thex-coordinate of the left side of the bounding box,double getXMax()returns the maximumxcoordinate of the blob—i.e, thex-coordinate of the right side of the bounding box,double getYMin()returns the minimumycoordinate of the blob—i.e, they-coordinate of the top of the bounding box,double getYMax()returns the maximumycoordinate of the blob—i.e, they-coordinate of the bottom of the bounding box,boolean contains(double x, double y)which returnstrueif the point(x, y)is contained in theBlob,double estimateArea(int nPoints)which uses a Monte Carlo simulation to estimate the area of theBlob. The parameternPointsis the number of sample points the simulation should use, and the returned value should be computed according to Equation (3) above.
In order to generate random points for your Monte Carlo simulation, you can use the Random class—see the Random documentation here. Specifically, to generate a random point (x, y) in the bounding box of your blob, it is enough to generate x and y separately using the nextDouble() method for Random (doing some transformation to ensure these numbers have the appropriate maximum and minimum values).
What to submit
Submit all code needed to run your program to the Moodle site by Friday, April 16th, 11:59 AoE. Additionally, please fill out the survey linked to from the Moodle submission site.
Grading
The lab will be graded on a 3 point scale as follows:
- 3 Everything compiles and runs as specified in this document; code is fairly readable and contains comments briefly describing the main functionality of methods defined/larger chunks of code.
- 2 The program produces more-or-less correct output, but is sloppy/hard to read; comments may be there, but are not helpful.
- 1 Program compiles, but is far from producing the expected output and/or does not run as specified; comments unhelpful or absent.
- 0 Program doesn’t compile or outputs garbage; no comments explaining why.
Additionally, extra credit will be awarded for early submissions (up to 4 days early) as specified in the course syllabus.
Extensions
Here are a couple of suggested extensions:
- Make a program that draws your
Blobon the screen, together with its bounding box. Note that you will need to transform the coordinates of theBlob(stored asdoubles) to make an appropriately sized image on the screen. You may want to modify the defaultdraw()methods inAbstractShapeandCircleso that it allows you to rescale the image. - If extension 1 isn’t enough, you might also want to modify the program so that the sampled points are also drawn on the screen with different colors to indicate “hits” and “misses”.
- Generalize the
Blobto consist of more shapes! Make otherAbstractShapes such as rectangles (easy), triangles (medium), or general polygons (hard). YourAreaTestershould still compute the correct (estimate of the)Blob’s area.
If you complete an extension, please include a README file with your submission explaining what you did and how to use it.