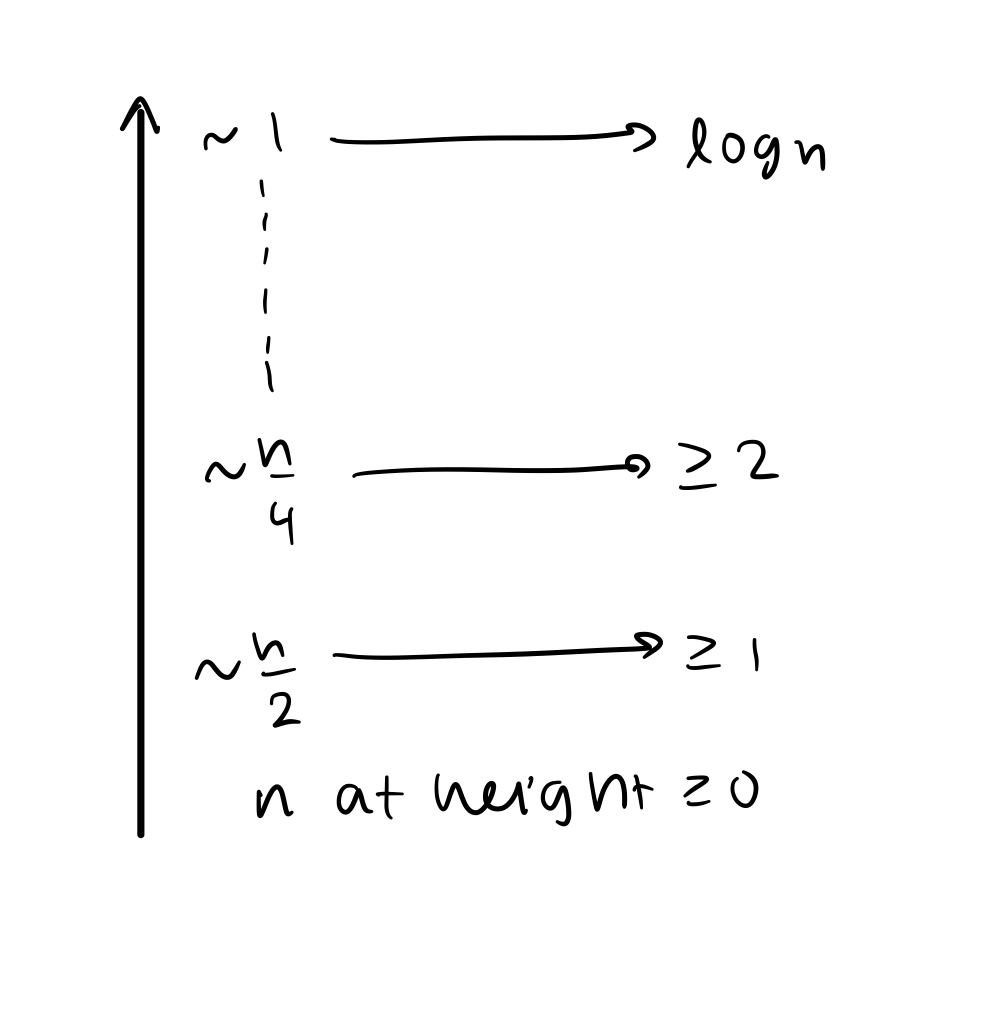Lecture 15

A template for scribe notes

Scribes:

  • Tanmai Pathak

Lecture 15

  1. Skiplists

Announcements

  • Quiz 03 (due Tuesday)
  • Assignment 5 posted tonight (no data structures!)

Last Time

Sorted Sets: S = {x_0, x_1, … , x_n} where x_0 < x_1 < … < x_n

  1. Linked list of nodes: all operations are O(n)
  2. Sorted array: add/remove are O(n), find is O(logn) because of binary search
  3. Unbalanced BST: all operations O(h)
    • h = height of tree
      • depends on order of operations
    • h <= n-1 (always)
    • random adds h is typically O(logn)
  4. Balanced BST (AVL tree): operations are still O(h) but maintain h = O(logn) which is always true

Going Forward

Randomized data structures

  • Introduce randomness
  • Probabilistic guarantees
    • good behavior, most of the time independent of what user is doing
  • Often: simpler solutions than deterministic

Skiplists

LinkedList:

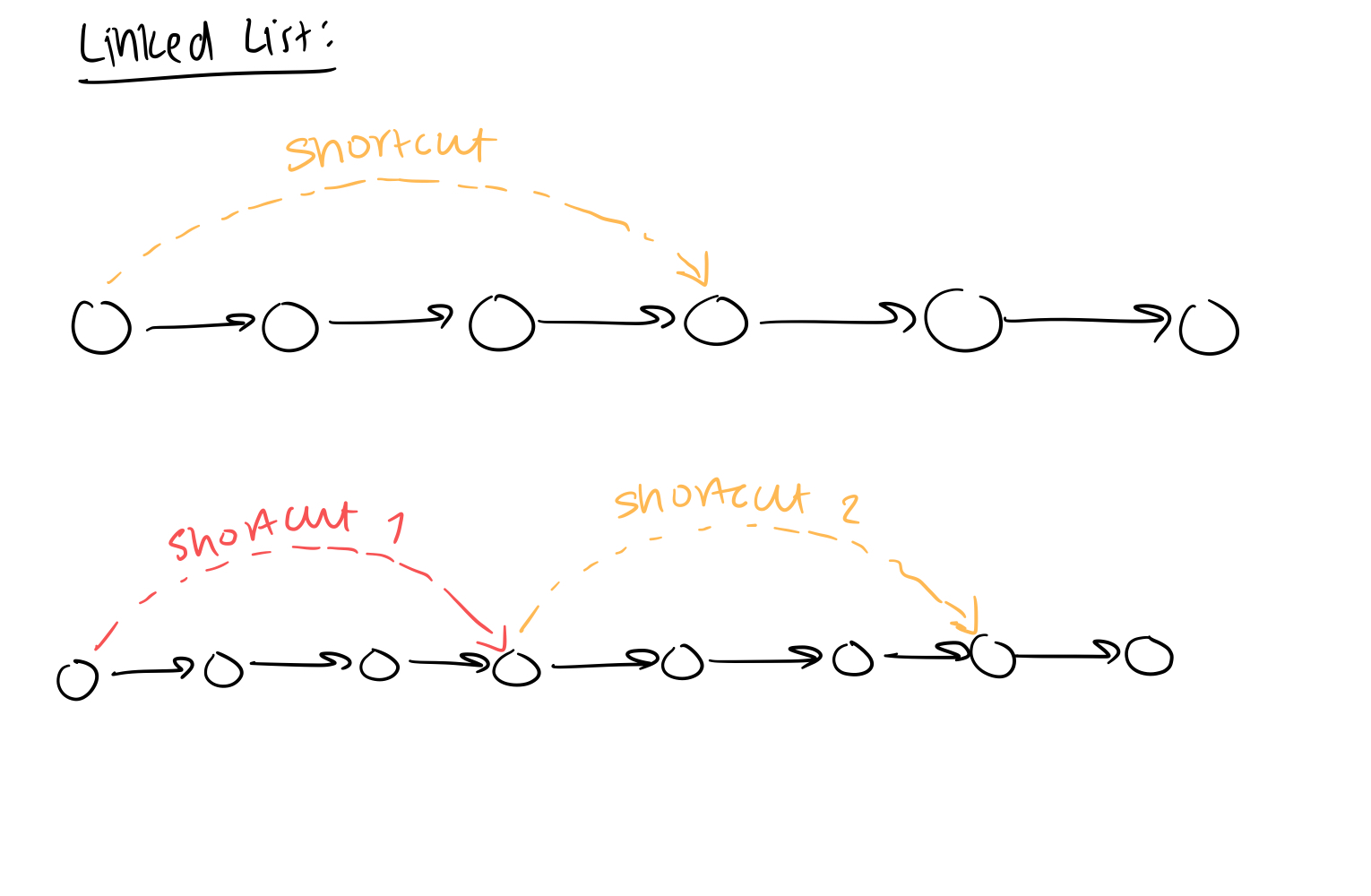
Image_1

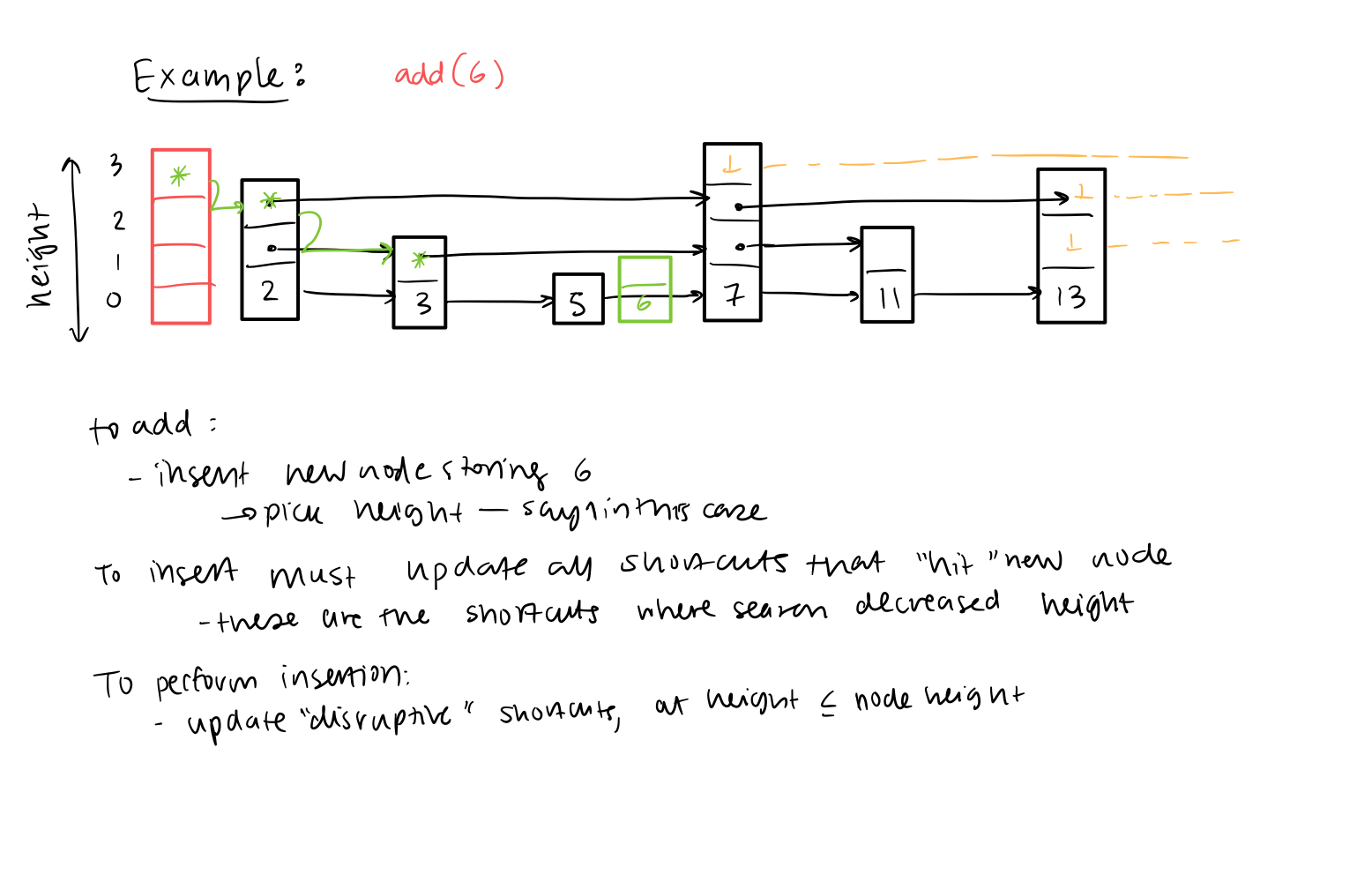
  • Adding shortcuts might improve search time
  • When adding and removing, the shortcuts have to be changed
    • might be really expensive to maintain the shortcuts

Idea:

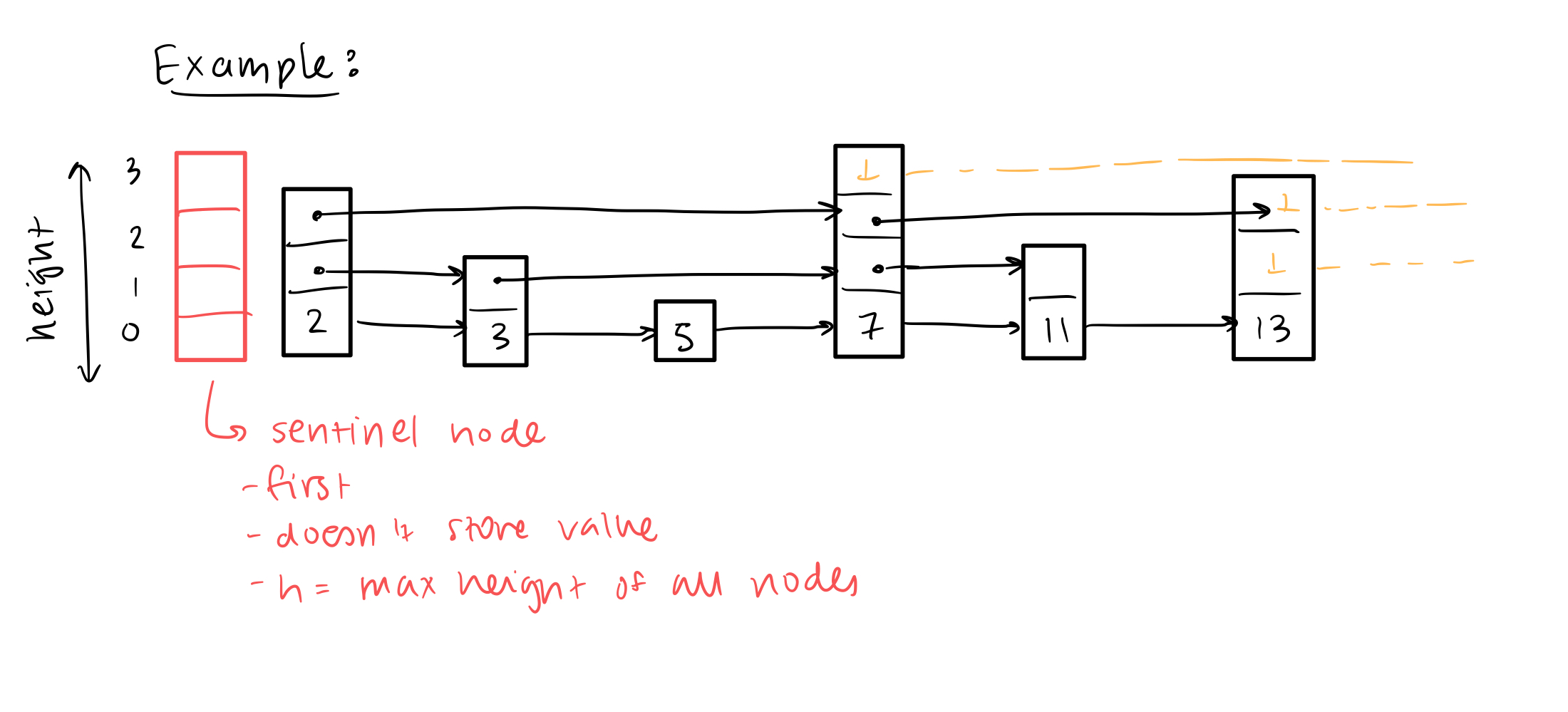
  • Associate height to each node
  • if node v has a height h, store a shortcut to next nodes of height at least h, h-1, …, 0
  • Sentinel node
    • first
    • doesn’t store value
    • h = max heigh of all nodes
  • More formally: each node v stores an array of h(v) “next” nodes next[i] = shortcut at height i
    • only applies to nodes that also have at least the same height as the nodes being pointed to

Image_2

How to find(x)?

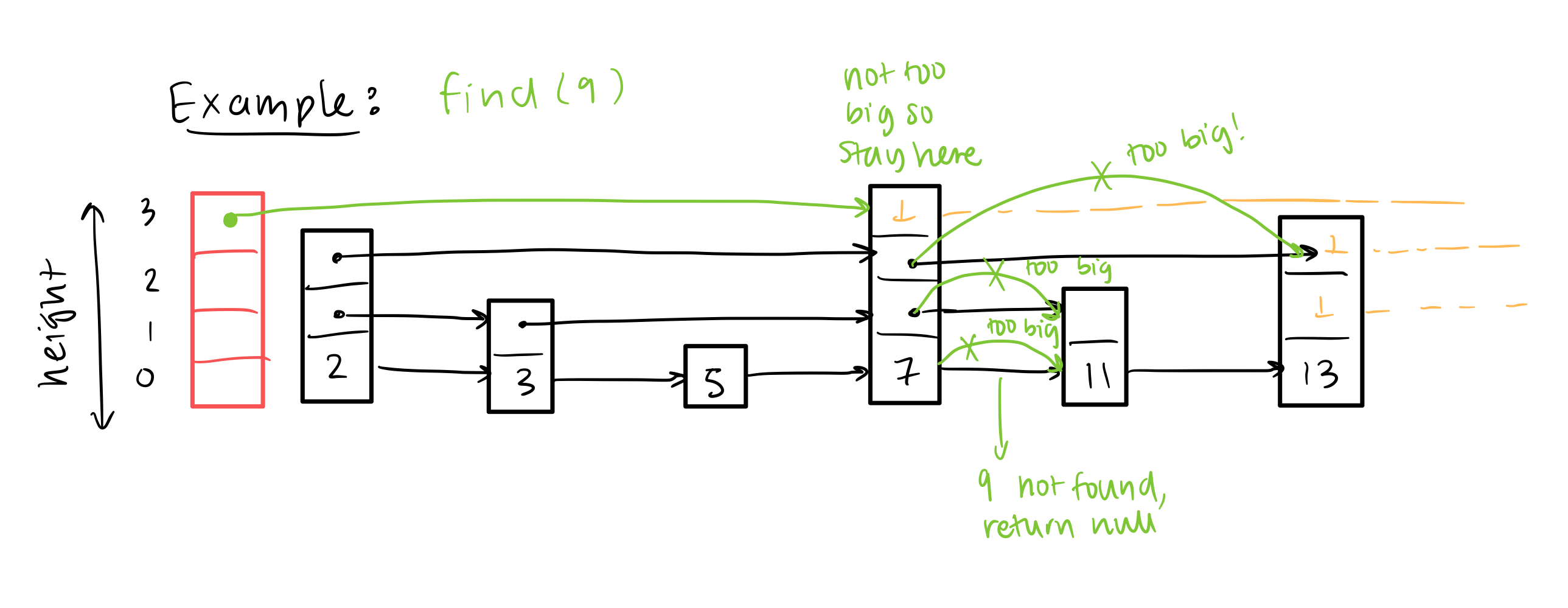
Image_3

Generally:

  1. Start at v = setinel node
  2. h = max height
  3. Find next node (w) at height >= h (next[h])
    • if value of w = x, return value of w
    • if value of w < value of x, update v = w
    • if value of w > value of x, decrease height and repeat step 3
    • if h < 0, return null

How to add(x)?

Image_4

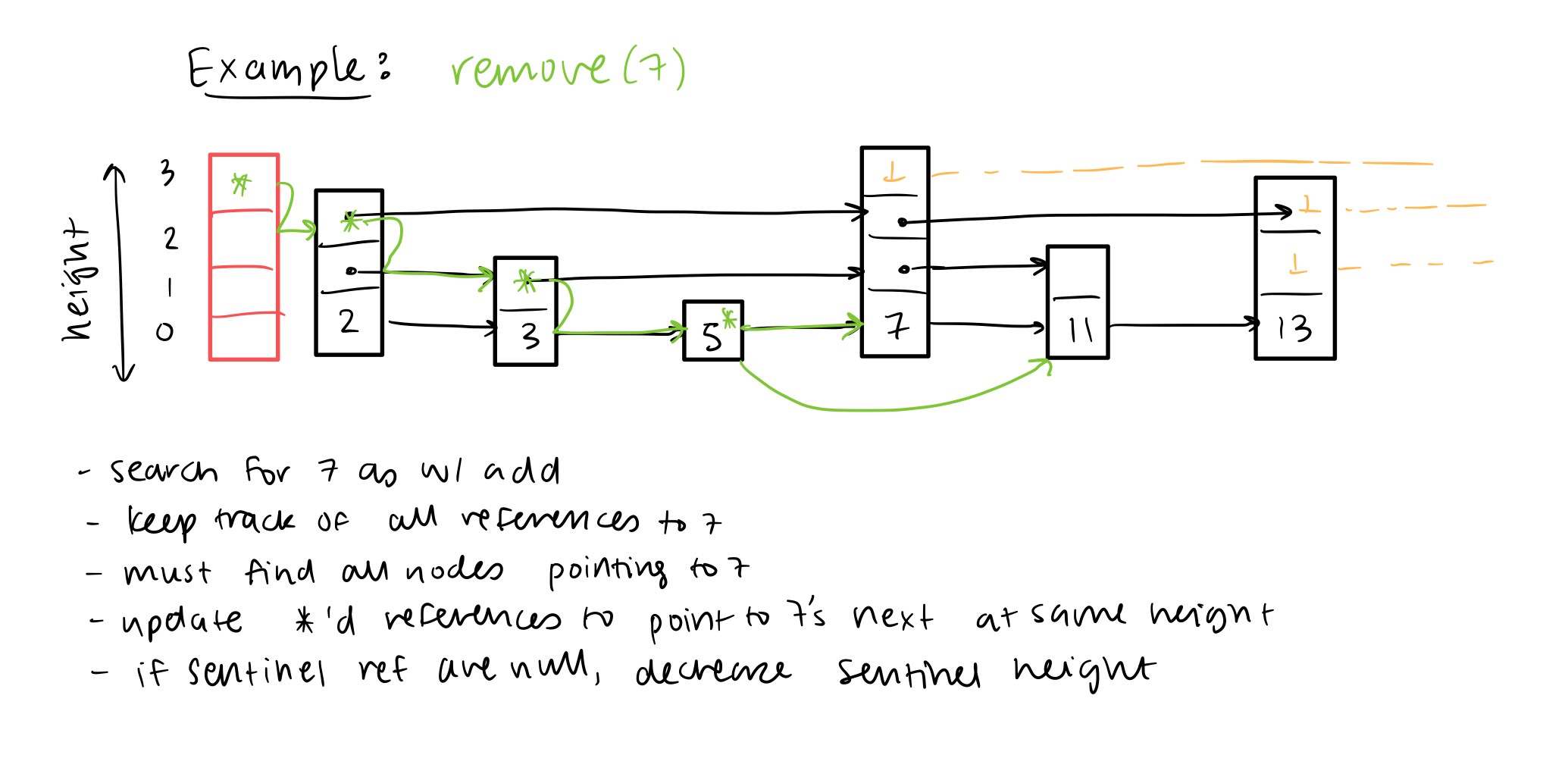
How to remove(x)?

Image_5

Lingering Question

How to choose height of new nodes?

  • What do we want?
    • hierarchical structure:
      • if “balanced BST - like”
      • one tallest node in the middle - height = h
      • two (or few) nodes at height h - 1
      • fourish at height h - 2
      • n at heigth >= 0
  • Random process to generate height:
    • flip coins: each flip is H/T (equally likely)
    • h = # of T before first H
  • Then:
    • about n have height 0
    • about 1/2n have height >= 1
    • about 1/4n have height >= 2
    • about 1/8n have height >= 3

Image_6