Lecture 13: Template
A template for scribe notes
Scribes:
- Tanmai Pathak
Lecture 13
- Empirical Comparison
- Unbalanced BST vs AVL Trees
- Heaps and Priority Queues
- Implementing a Heap
Announcements
- Return Q1, Q2
- HW 04 Posted (Due Thursday)
- Quiz 03 Next Week (on trees)
Last Time
Height-balanced tree: AVL tree
Property: T is AVL if every node v is height-balanced:
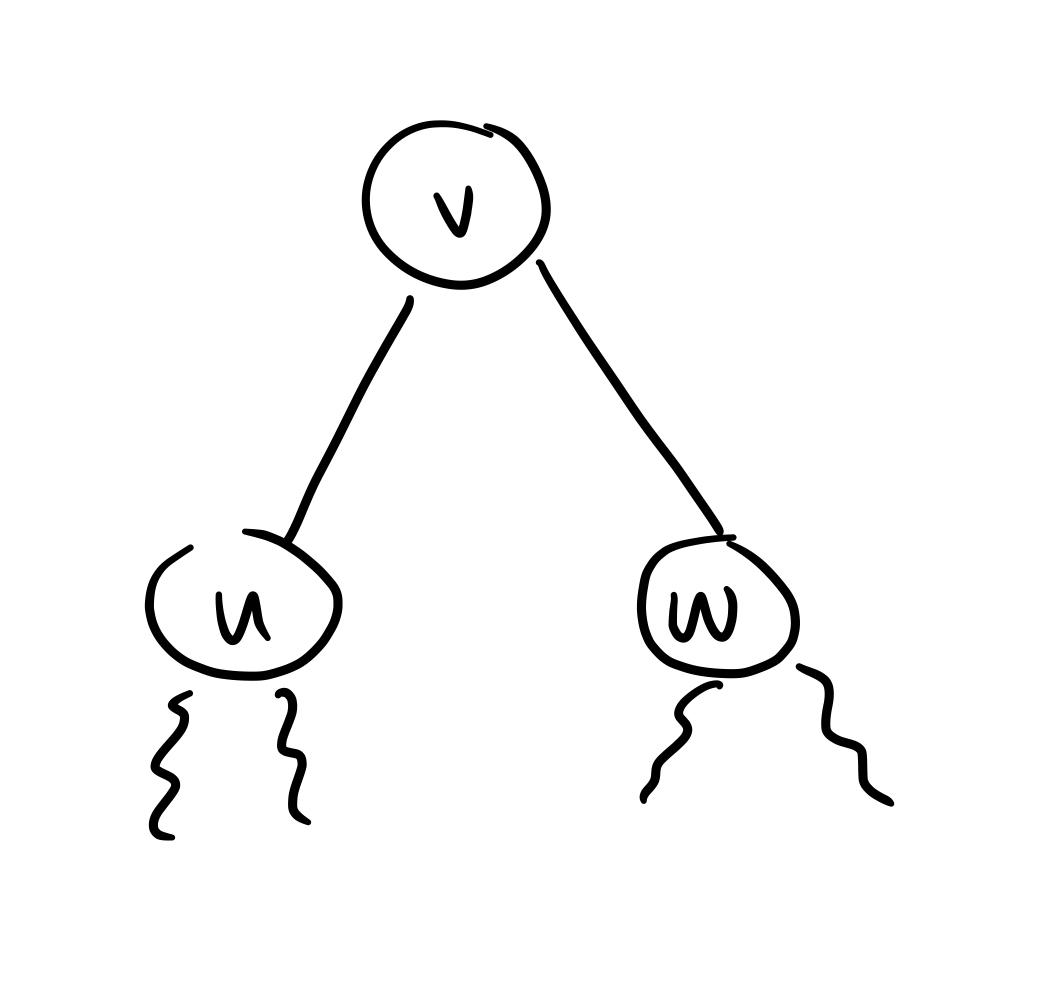
| We have | h(u) - h(w) | <= 1 |
Consequence: If T is AVL tree with n nodes, then h(T) = O(logn)
Consequence: If T is AVL then find, add, remove can be performed in O(logn) time.
Updating:
If T was AVL before add/remove, then AVL property can be restored in time O(logn) after performing operation:
- each node additionally store height –> see lecture 13 code for implementation
- update heights of ancestors on add/remove (O(logn) time)
- check for imbalance
- restore balance by restructuring (O(logn) time)
Conclusion: We can implement sorted set ADT where all operations can be performed in O(logn) time.
Priority Queue and Sorted Set
Previously:
- BST –> sorted sets (add, find, remove)
- Queues –> access first-in, first-out (FIFO)
- Queue specializes SSet - only add largest (latest element), and only remove smallest (oldest element)
Today: further restriction of sorted set functionality, still generalizing a Queue
- Priority Queue
- add/remove elements
- for add –> specify priority for element
- for remove –> always remove highest priority element
- Ex: to-do list with relative importance of tasks
- add/remove elements
Priority Queue from Sorted Set?
- Define Pair datatype that stores:
- priority (k = key)
- element (v = value)
- (k, v)
- Comparison of pairs:
- (k, v) < (k’, v’) if k < k’
- SSet stores Pairs
- to add, v with priority k, create pair (k, v) and add to SSet
- Removal: removeMin?
- removeMin for SSet returns (k, v)
- Priority Queue just returns v
- Note: higher the priority, smaller numerical value of key
Complete Binary Trees (CBT)
T is a CBT of depth d if:
- all nodes at depth <= d-2 have 2 children
- at most 1 node at depth d-1 with 1 child, and it is left child
- if u and v are at depth d-1, u to left of v and v has a child, then u has 2 children
This implies there is a unique location to add a new node to any CBT
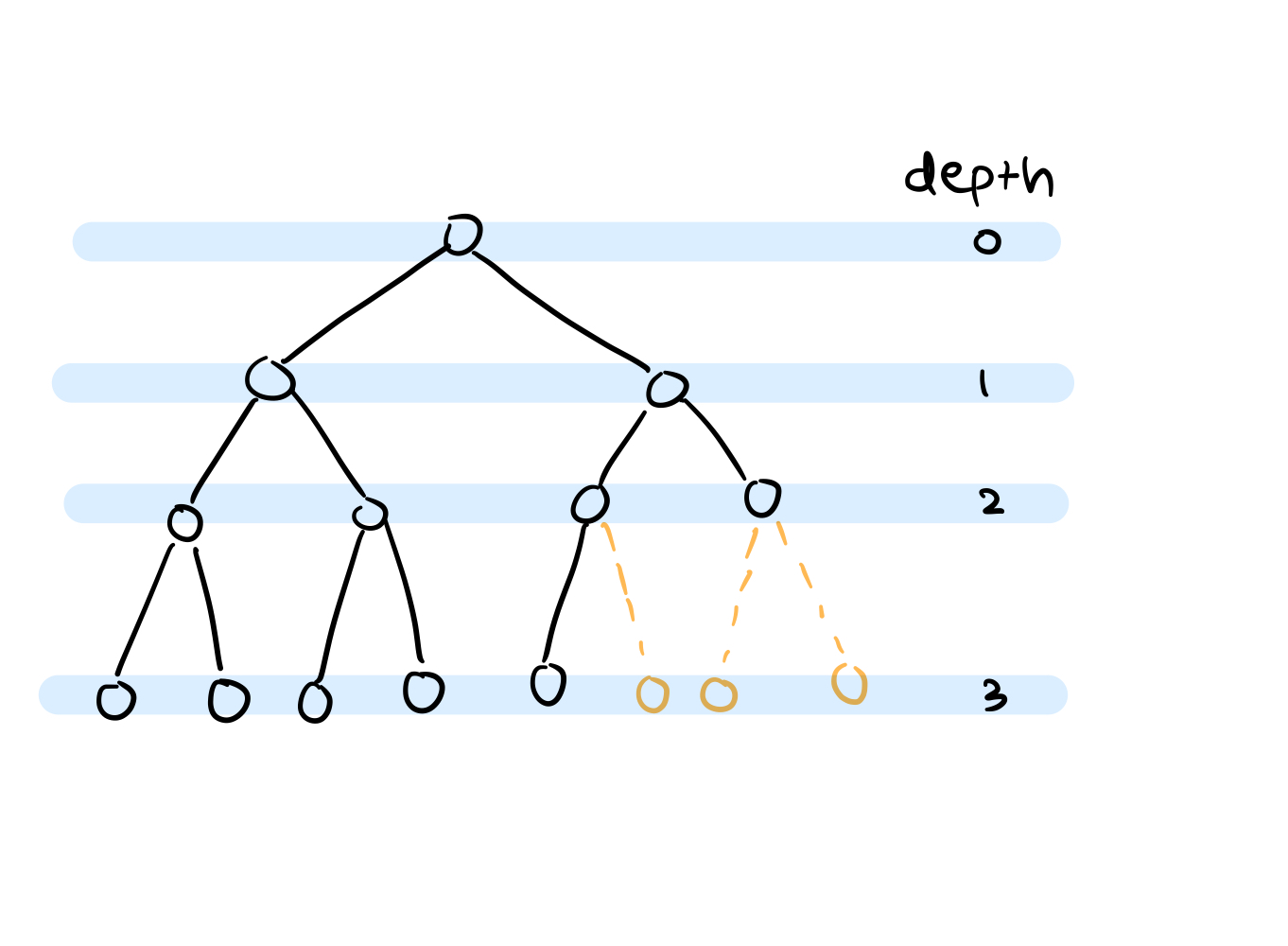
Observation: A CBT of depth d has at least:
\(1 + 2 + 2^2 + 2^3 + ... + 2^{d-1} + 1\) (1 represents at least 1 leaf at depth d)
\[(2^d - 1) + 1 = 2^d\]Therefore: If T is a CBT with n nodes, then depth(T) <= logn
Binary Heap
- a binary heap is a CBT where each node stores a comparable element and if

(v has children u and w) then v <= u and v <= w
Why we like Heaps
- very balanced
- with our Priority Queue, we want to find the smallest element which has the highest priority, which is root of a Heap
- very quick access to the smallest element
How to add(2)?
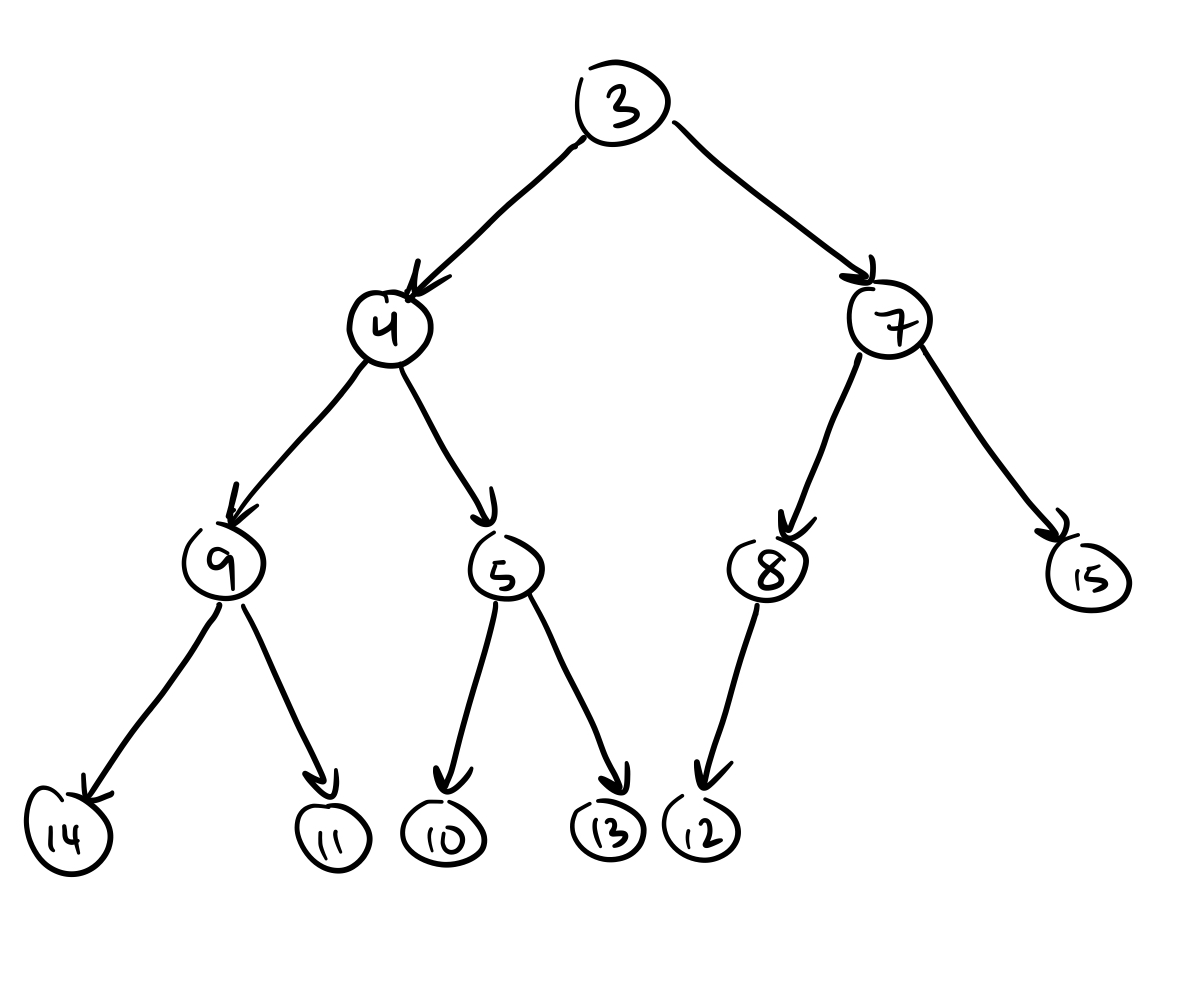
- 2 must end up at root
- Other elements are pushed down to the unique space for new node
Implement with “bubble up” procedure
- Add 2 at unique new node location
- Repeat: if new value is smaller than parent, swap, then move to parent
Work: convince yourself that this maintains Heap property
How to remove min?
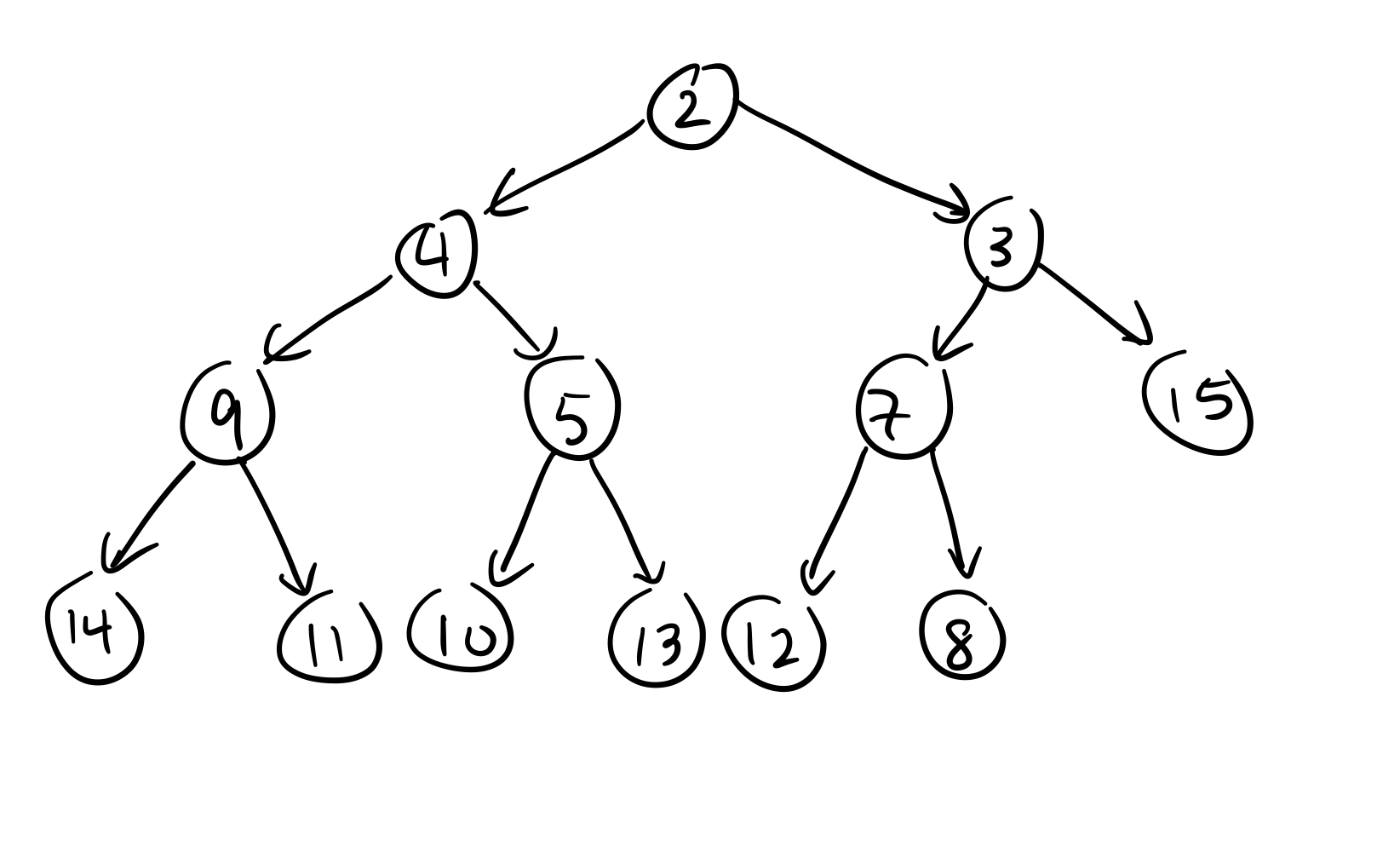
- Copy value at “last” leaf (in this case 8) to root and remove leaf.
- Then “bubble down”
- Swap root value with smaller child
- Repeat: until the copied value is smaller than both children