Lecture 10: Balancing BSTs
Scribe notes on balancing binary search trees
Scribes:
- Andy Arrigoni Perez
- Sawyer Pollard
- Luxin Sun
- Cesaire Mugishawayo
Overview:
- Defining height balance
- Benefits of balance
- Maintaining balance efficiency
- Add
- Remove
Section 1: Defining height balance
Goal: Since find, add and remove run at O(h) (Where h is the height of the tree, we want to support the add/remove methods to maintain h as small as we can.
Definition of height:
Let \(v\) be a node in a binary tree.
Then, \(h(v)= height\) (Distance to the most distant descendant leaf)
Note: Convention is that \(h(null) = -1\)
Observation:
If \(u = v.left\) and \(w = v.right\),
then \(h(v) = 1 + max(h(u), h(w))\)
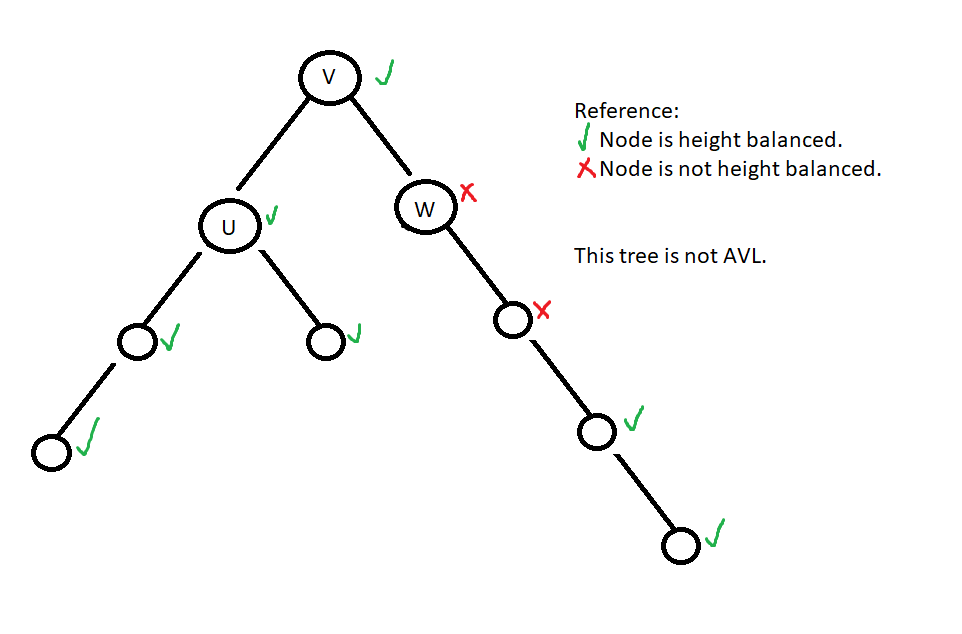
Definition: Node \(v\) is height balanced if the heights of \(v\)’s children differ at most by 1. Formally: \(\lvert h(u) - h(w) \rvert \leq 1\)
Importantly, a binary tree T is (height) balanced or AVL (named for its creators Georgy Adelson-Velsky and Evgenii Landis) if all nodes in T are height balanced.
Example:
Section 2: Benefits of Balance
Goal: If T is balanced (or AVL), then its height \(h\) is \(O(log(n))\) where \(n\) is the number of nodes in the tree.
Roundabout Method: Consider \(m(h) = \text{minimum number of nodes in AVL tree of height h}\)
If \(n \leq m(h)\), then the height of the tree is at most \(h\).
What is \(m(h)\) for small values? m(0)=1 | \(m(h)\) values for small \(h\) | |–| | \(m(0) = 1\) | | \(m(1) = 2\) | | \(m(2) = 4\) | | \(m(3) = 7\) | | \(m(4) = 12\) | | \(m(5) = 20\) |
What can we say about the structure of an AVL tree of height \(h\) with a minimal number of nodes? (when height of the tree is at least 2)
Firstly,
\[m(h) = 1 + m(h - 1) + m(h - 2)\](Note: \(m(h - 1) > m(h - 2)\))
So,
\[m(h) > 2 * m(h - 2 > 4*m(h-4) > 8*m(h-6) > \ldots\]This pattern can be generalized to: \(m(h) > 2^i * m(h - 2i)\)
If, \(i=\frac{h}{2} - 1\)
(Note: “round up” \(\frac{h}{2}\) to the nearest integer.)
Then, \(h-2i\) can only be \(0\) or \(1\).
So,
\[m(h - 2i)= m(0) \text{ or } m(1) = 1 \text{ or } 2\] \[m(h) \leq 2^i * m(0 \text{ or } 1)\] \[m(h) \leq 2^{\frac{h}{2} - 1}\]Taking \(log\) of both sides:
\[log(m(h)) \geq \frac{h}{2} - 1\] \[2 * log(m(h)) + 2 \geq h\]Conclusion: If T is an AVL tree with \(n\) nodes and height \(h\), then:
\[2 * log(m(h)) + 2\] \[h \leq 2 * log(n) + 2\]✅ \(h = O(log(n))\)
Section 3: Maintaining Balance
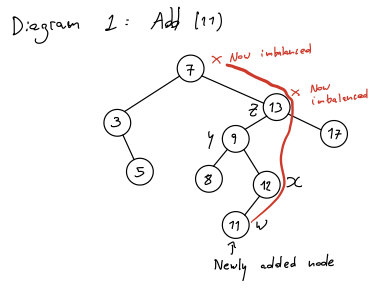
When can imbalance occur?
- Only at an ancestor of a newly added node.
- Only in at most \(h\) nodes, since the tree was previously balanced, and the imbalance only occurs at the ancestors of the newly added node.
Let:
\[W = \text{newly added node causing an imbalance (11 in our example)}\] \[Z = \text{deepest node where imbalance occurs (13 in our example)}\] \[Y = \text{child of z in the direction of W (9 in our example)}\] \[X = \text{child of y in the direction of W (12 in our example)}\]Because of the properties of BSTs, we know that: \(Y < X < Z\)
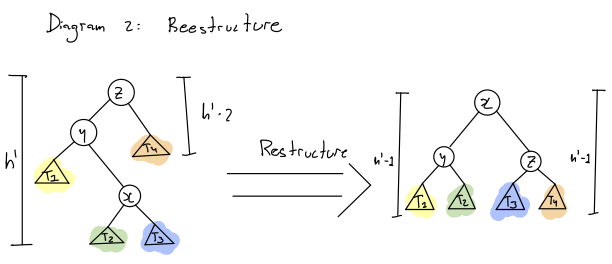
What we want: (Picture of restructure)
Questions worth thinking about:
- Why does this restructure maintain BST property?
- Why does it restore balance?
- What is its running time?