Assignment 01
Deque implementions with arrays and linked lists
Overview
In class, we saw the List abstract data type (ADT), as well as two
implementations: one using an array data structure, and the other using a linked list. We also saw three related ADTs—Stack, Queue, and
Deque—and how each can be implemented from any List
implementation. In this assignment, you will provide two more
implementations of a Deque using variations of an array and linked
list, respectively.
Pair Assignment
This assignment is a pair assignment. You will be randomly paired with a partner, and you will complete your work together. Please complete this survey in order to be assigned a partner.
Background
In this assignment, you will provide two implementations of the Deque ADT. The Deque is described in ODS, Section 1.2. See also Chapter 02: Array-based lists and Chapter 03: Linked Lists.
To complete this assignment, you will need to use two data structures that are variations of data structures we used in class: circular arrays and doubly linked lists.
Circular Arrays/Buffers
An array stores its elements sequentially in a contiguous block at indices \(0, 1, 2, \ldots, n-1\), where \(n\) is the size of the array. We often depict arrays as a block of cells storing elements \(0, 1, \ldots, n-1\) from left to right, like this:
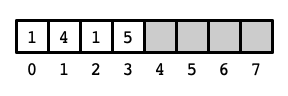
Above is an array of size 8 storing 4 elements with values \(1, 4, 1, 5\), respectively, at indices 0 through 3. It is often helpful, however, to view the elements of the array as if they are arranged in a circle or ring:
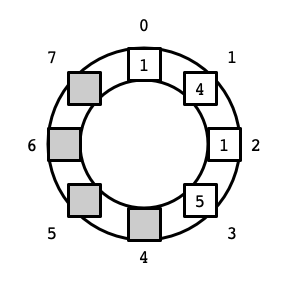
In particular, this view is useful for implementing a deque where elements can be added and removed from both sides of a contiguous block of elements in the array. In our first List implementation using an array, if we wanted to insert an element—say the value 3—before the first element in the list (at index 0), we needed to move all of the other elements to make room for the new element. Viewing the array as a circle makes it evident that there is another way: we can place the new element to the left of 0 at index 7 (assuming this position is not already occupied). Thus, we might store the list of elements \(3, 1, 4, 1, 5\) in the circular array as follows:
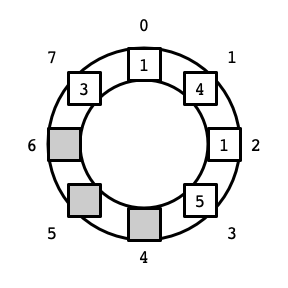
There are two slight complications. The first is that we now need to keep track of two indices: the upper (front) index, and the lower (back) index. In the example above, the lower index is 7 (storing the value 3), and the upper index is 3 (storing the value 5).
The second complication is that when we increase or decrease an index, we might go beyond the bounds of the original array. As the picture above indicates, this can be dealt with in a straightforward manner: if we increase past \(n - 1\) (going over the top of the circle counter-clockwise), we arrive at index \(0\). Symmetrically, decreasing an index from \(0\) brings us to index \(n - 1\). (Arithmetic in which \(0\) is the successor of \(n - 1\) and \(n - 1\) is the predecessor of \(0\) is known as modular arithmetic.) Here is a picture of the contents of the array in its traditional depiction as a block of cells:
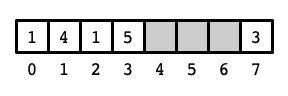
By storing elements in the circular array, elements can be added to and removed from either side of the block storing the contents of a deque without displacing the other elements. In this assignment, you will see that this approach yields significantly better performance of the data structure compared to our original array-based implementation of a deque.
Doubly Linked Lists
In class, we saw an implementation of a List using a linked list data
structure. While accessing and modifying elements at the head of a
linked list is efficient, accessing the “tail” of the list is not, as
all preceding elements must be traversed to reach the final node in the
list. A doubly linked list is modification of a linked list in which:
- references to both the head and tail nodes are stored, and
- each node stores references to both its next and previous nodes.
For example, the following figure depicts a doubly linked list storing the elements 1, 4, 1, 5.
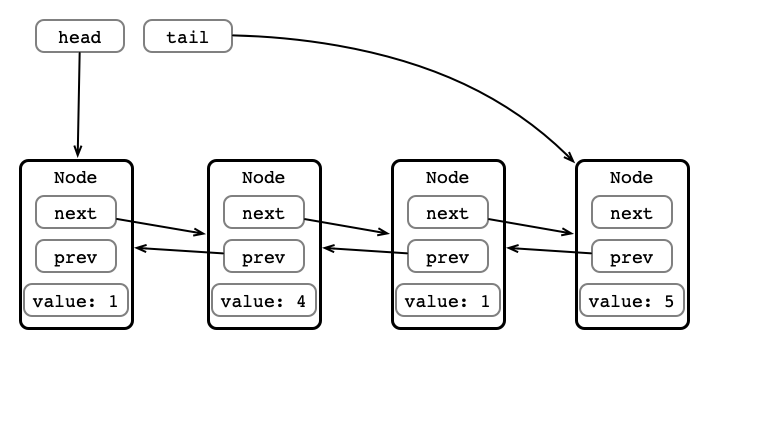
With a doubly linked list, both the head and tail elements can be accessed directly, so adding/removing elements at both ends of the data structure can be performed efficiently.
Code
Download this archive containing the following files:
- Interfaces
SimpleDeque.javaSimpleList.java
- Utilities
DequeTester.javaCSVWriter.javaRunTimer.java
- Implementations
ArraySimpleList.javaLinkedSimpleList.javaASLDeque.javaLSLDeque.java
Your Task
For this assignment, you will write and test two implementations of the
Deque ADT:
CADeque.java, which implementsSimpleDequeusing a circular array, andDLLDeque.java, which implementsSimpleDequeusing a doubly linked list.
Be sure to test the correctness of your implementation using the provided DequeTester.java. The provided version of DequeTester currently test the (provided) LSLDeque implementation, so you’ll need to add your implementation to the test. For example, you can test CADeque by setting
1
SimpleDeque<Integer> deque = new CADeque<Integer>();
at the beginning of the main method in DequeTester.java.
You should also write a program that tests the performance of your SimpleDeque implementations. Specifically, it should be able to measure the (average) running times of the SimpleDeque operations for a range of instance sizes (i.e., for various numbers of elements stored in the deque). You do not need to submit this program, but you should use its output to answer the questions below. For example, you should test the amount of time required for addFirst and addLast for various sizes of deques—say around 50 different values—to get a sense of the trend of how these running times depend on deque size.
You may find the examples in class (found in SimpleLists.zip) helpful. Also, CountTimer.zip contains a simpler demonstration of the usage of RunTimer and CSVWriter to measure and record running times of methods.
Questions
Please answer the following questions about your programs. Be sure to support claims with evidence (e.g., running times).
-
Consider the
addFirstandaddLastmethods for yourCADeque. How does the running time of these methods depend of the size of the deque? -
Consider the
addFirstandaddLastmethods for yourDLLDeque. How does the running time of these methods depend of the size of the deque? -
How do the running times of
addFirstandaddLastcompare between yourCADequeandDLLDequecompare with each other? Which is faster for large deques? For small deques? -
How do the running times of
addFirstandaddLastcompare between your implementations and the provided list-based implementations,ASLDequeandLSLDeque?
What to Submit
You should submit:
CADeque.javacontaining yourSimpleDequeimplementation using a circular array,DLLDeque.javacontaining yourSimpleDequeimplementation using a doubly linked list, andresponses.mdcontaining your responses to the questions above.
You may include other files linked to from responses.md, such as graphs that indicate the running times for your tests.
Evaluation
Your submission will receive a score out of 10 points, broken down as follows:
- 3 points each for
CADeque.javaandDLLDeque.java.- code compiles, runs, and passes all tests in
SimpleDequeTester.java - code is well organized and documented with comments
- code compiles, runs, and passes all tests in
- 4 points for responses to the questions above