Lecture 37: Consensus III & Final Thoughts

COSC 273: Parallel and Distributed Computing

Spring 2023

Annoucements

1. Final Submissions: Tuesday, 05/09 by 5:00pm
   • documentation = 40% of grade
   • code style = 10% of grade
     • remove all debugging messages!
   • test on cluster (timeout/compile errors)
2. Assignment/Quiz grading this week

Leaderboard 3

Primes Task (baseline 58810ms):

1. The AMA (2024ms)
2. Test Group Name Please Ignore (2217ms)
3. IsaM (2222ms)
4. Team 2 (2295ms)

Sorting Task (baseline 8034ms):

1. Deadlock Dodgers (1309ms)
2. MRC (1356ms)
3. Daily Mammoth (1451ms)
4. Benchmark (1509ms)

Binary Consensus

Setup: $n$ processes with binary inputs

• Agreement: all processes output the same value
• Validity: if all systems have the same input, they all output that valuex
• Termination: all (non-faulty) processes decide on an output and terminate after a finite number of steps

Bivalent & Critical Executions

An execution $E$ is…

• …bivalent if the final output is not yet determined
• …critical if the execution is bivalent, but no extension

Outline of Proof of FLP

Assume only 2 processes, $P_0$ and $P_1$

1. Start from a critical execution $E$
   • $E$ is bivalent, but any extension is univalent
2. Consider all possibilities for next step:
   • both threads read for next step
   • one thread reads, the other writes
   • both threads write
3. Show that in any case, we contradict either criticality of E or correctness of protocol

Assumptions

Without loss of generality:

1. There are two processes $P_0$ and $P_1$
2. $E$ is a critical state
   • if $P_0$ has next step, resulting execution is $0$-valent
   • if $P_1$ has next step, resulting execution is $1$-valent

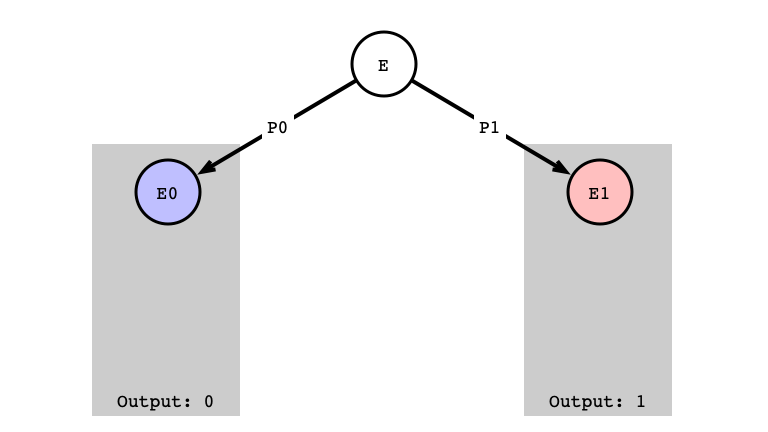
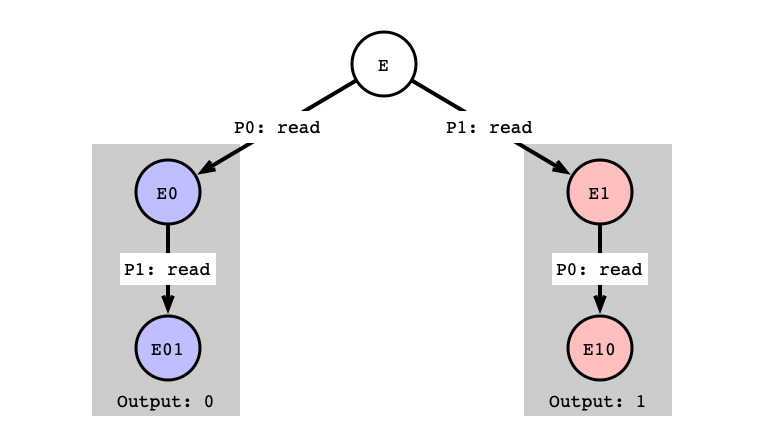
Case 1: read/read

Assumption: next operations for both $P_0$ and $P_1$ are read

• Start from critical state $E$
  • if $P_0$ steps next, output is 0
  • if $P_1$ steps next, output is 1

read/read

read/read Next Step

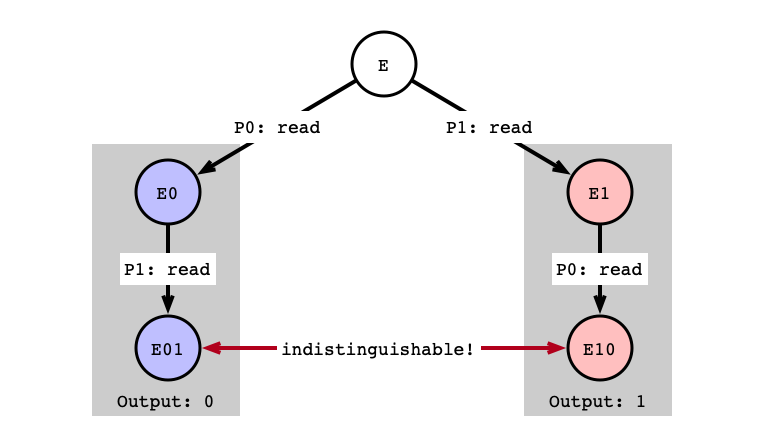
read/read Problem

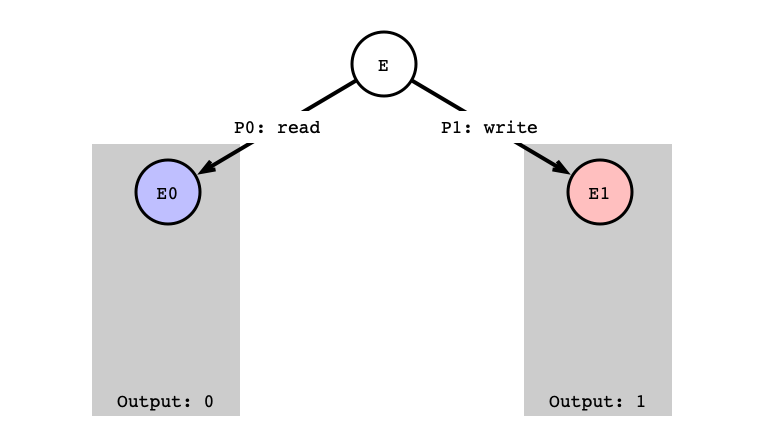
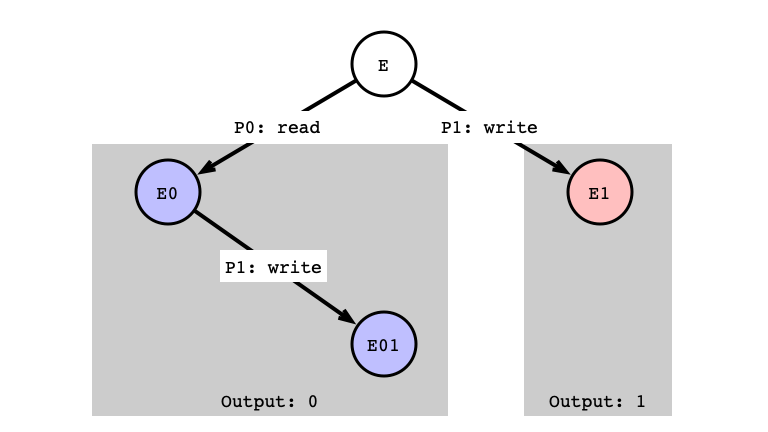
Case 2: read/write

Assumption:

• $P_0$’s next step is read

• $P_1$’s next step is write

• Start from critical state $E$
  • if $P_0$’s read step is next, output is 0
  • if $P_1$’s write step is next, output is 1

read/write Setup

read/write Next Step

read/write Indistinguishable

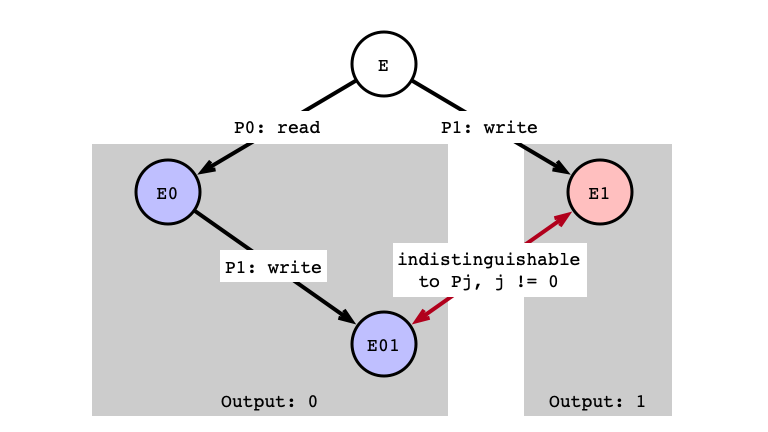
read/write $P_0$ Crashes

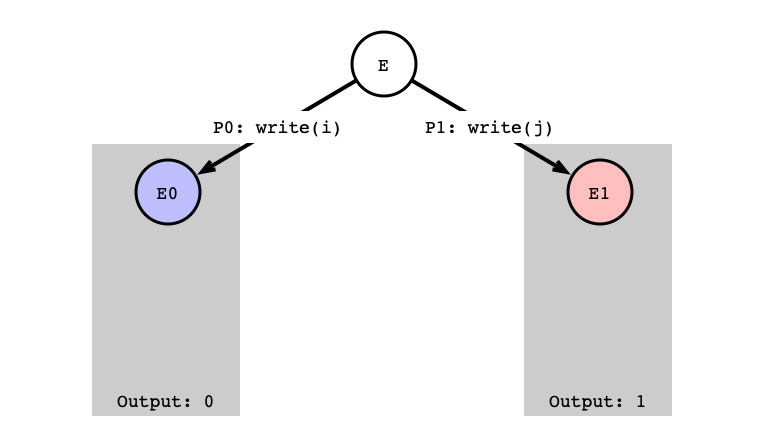
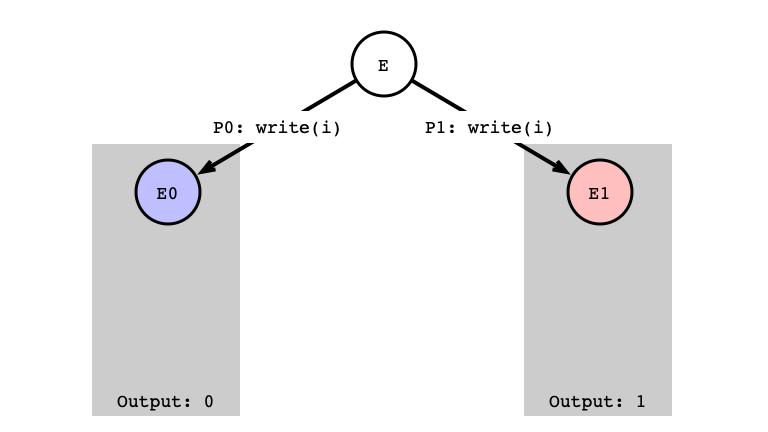
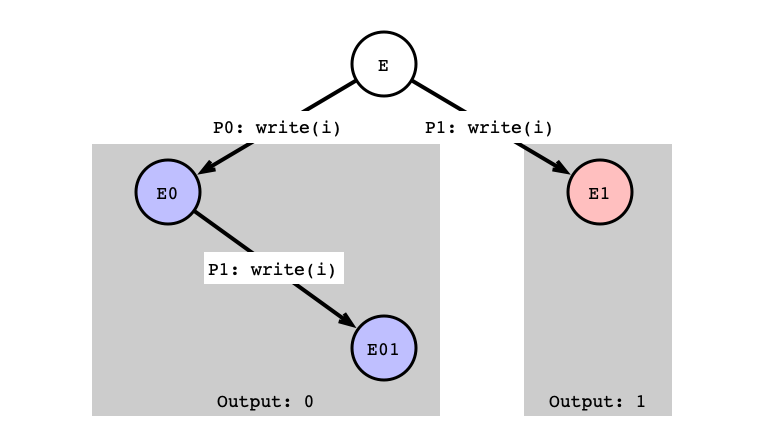
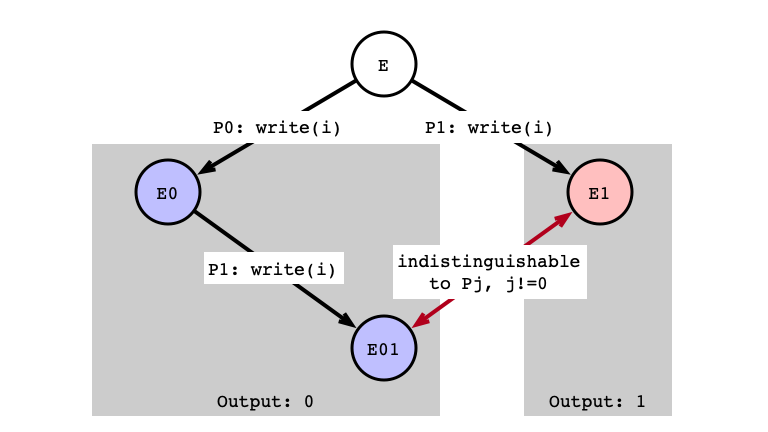
Case 3: write/write

Assumption: next operation for both $P_0$ and $P_1$ is write

Subcases:

• Sub-case a: write to different registers
• Sub-case b: write to same register

write/write Different Registers

write/write Next Step

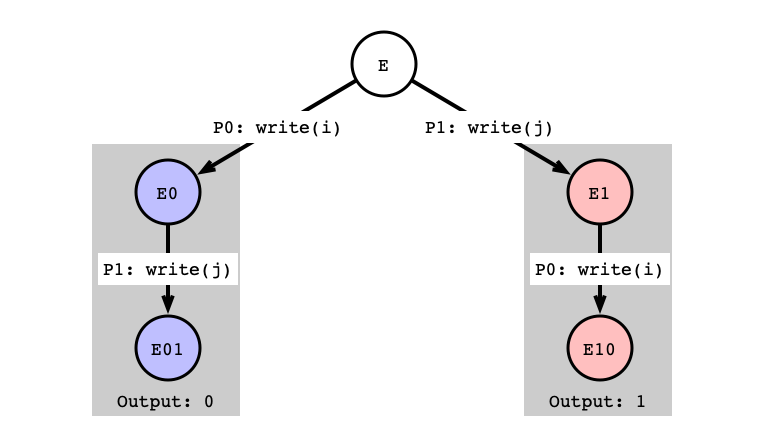
write/write Indistinguishable

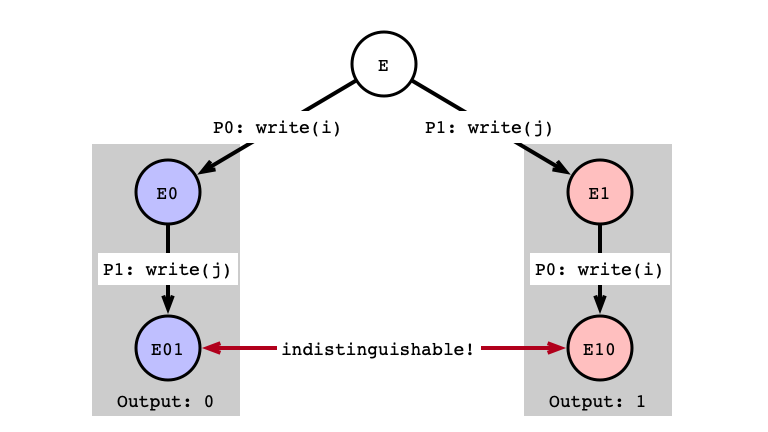
write/write Same Register

write/write Next Step

write/write Indistinguishable

Conclusion

In general:

• Indistinguishable executions produce same output

Assuming a wait-free consensus protocol using only read/write registers:

1. Showed there is a bivalent initial state
2. Showed there is a critical execution
3. Given a critical execution
   • found indistinguishable states that must give different outputs
   • this is a contradiction!

Consensus is Impossible?

Well not quite!

• We just proved impossibility in our computational model!
  • atomic read/write registers
  • wait-free (or faults)
  • nasty scheduler!

Does the Model Reflect Reality?

• single CPUs have stronger primitives!
  • compareAndSet
  • …
• we might have better schedulers
  • round-robin/synchronous
• computation could be distributed
  • how to implement compareAndSet for a communication network?
• faults could be worse
  • Byzantine faults

Implications

1. Atomic read/write registers are insufficient to solve fundamental tasks in parallel computing
   • this drives the development of hardware primitives (e.g. CAS)
2. We can quantify the computational power of primitive operations
   • read/write registers have consensus number 1
   • FIFO queues have consensus number 2
     • given wait-free queues, 2 threads can solve consensus (How?)
     • $\implies$ cannot implement concurrent queues with read/write registers
   • Can use compareAndSet to achieve consensus (How?)

Coda: Four Morals

1. Parallelism is Powerful

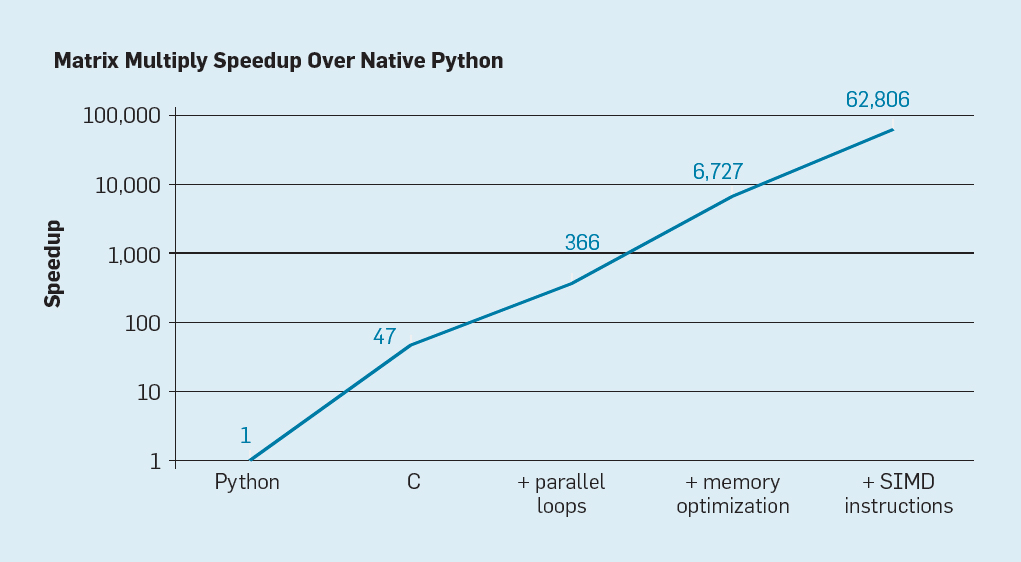
2. Communication is Costly

3. Synchronization is Subtle

• locks
• atomic operations
• concurrent data structures
• progress and correctness
• consensus

4. Definitions & Proofs are Critical

• computing technology affects every aspect of modern life
• systems are built upon computational primitives (e.g., consensus)
• to reason about effects of a system, we must clarify
  1. desired outcomes (definitions)
  2. component capabilities (assumptions)

Thank You!