Lecture 36: Consensus II
COSC 273: Parallel and Distributed Computing
Spring 2023
Annoucements
- Quiz due tonight
- Leaderboard 3 submissions, run Sunday morning
- Final Submissions: Tuesday, 05/09 by 5:00pm
- documentation = 40% of grade
Leaderboard 2
Primes Task (baseline 58810ms):
- The AMA (2070ms)
- Test Group Name Please Ignore (3530ms)
- Deadlock Dodgers (4467ms)
Sorting Task (baseline 8034ms):
- Deadlock Dodgers (1548ms)
- MRC (1550ms)
- Benchmark (2013ms)
Binary Consensus
Setup: $n$ processes with binary inputs
- Agreement: all processes output the same value
- Validity: if all systems have the same input, they all output that valuex
- Termination: all (non-faulty) processes decide on an output and terminate after a finite number of steps
Theorem (FLP, 1985). There is no algorithm that achieves consensus in the presence of even a single faulty process.
Today
We’ll prove:
Theorem. There is no wait-free protocol for consensus for shared memory with atomic read/write access.
- wait-free means each process completes in a bounded number of steps, indpendent of actions of other threads
Game Plan
Theorem. There is no wait-free protocol for consensus for shared memory with atomic read/write registers.
- Define indistinguishability of executions
- Lemma 1. indistinguishable executions have same results
- Define bivalent execution
- the final output (all 0s or all 1s) has not yet been determined
- Lemma 2 Show there is a bivalent initial state
- Define critical executions: if any process takes a step, then output is determined
- Lemma 3 Every protocol has a critical execution
Executions
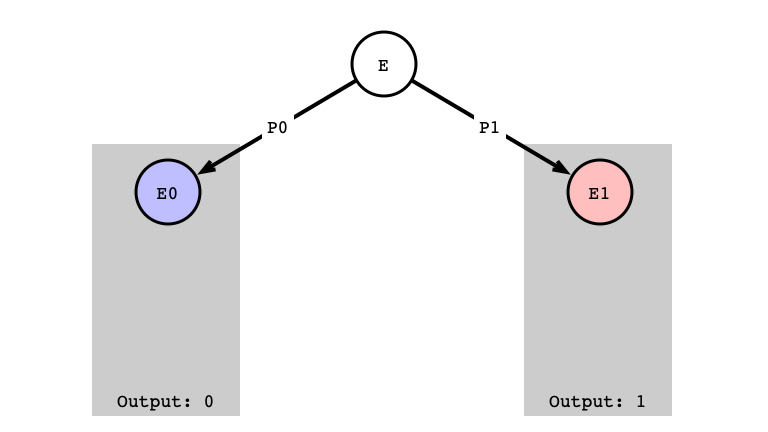
An execution $E$ of algorithm $A$ specifies
- Inputs of all processes
- Sequence of steps taken by processes
- read, write, terminate, crash
Executions may be incomplete
- Not all nodes have terminated/crashed yet
- encodes current state/history of execution
Executions may be extended by scheduling more steps
Example of Execution $E$
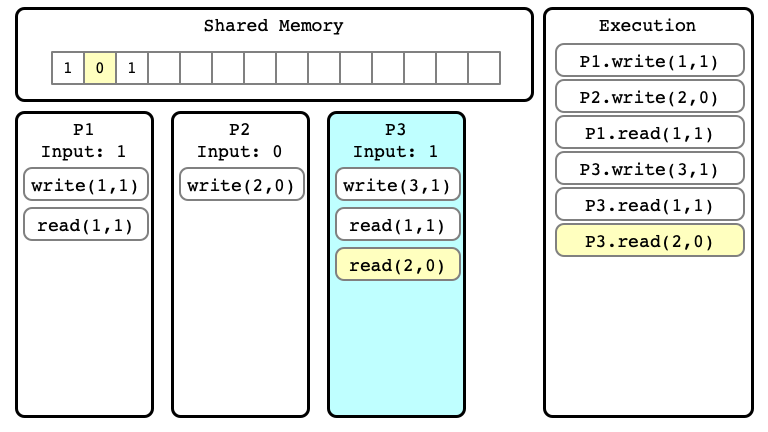
Indistinguishable Executions
- $E$ and $E’$ are executions
- they are indistinguishable at process $P_i$ if in $E$ and $E’$:
- $P_i$ has same input
- sequence of read/write operations performed by $P_i$ are same
- the sequence of values read and written by $P_i$ are the same
First Important Observation
Lemma 1. If executions $E$ and $E’$ are indistinguishable to process $P_i$ then:
- If $P_i$ has not yet terminated, then $P_i$’s next step will be the same in any extension
- If $P_i$ has terminated, then $P_i$’s output is the same in $E$ and $E’$
Bivalent Executions
- Consider a (hypothetical) wait-free consensus protocol $A$
- Let $E$ be an execution of $A$
We say that $E$ is…
- $0$-valent: in every extension of $E$, all processes output $0$
- $1$-valent: in every extension of $E$, all processes output $1$
-
bivalent if there exist
- an extension $E’$ of $E$ in which all processes output $0$
- an extension $E’’$ of $E$ in which all processes output $1$
Second Important Observation
Lemma 2. Suppose $A$ solves consensus. Then there is a bivalent initial state.
- Here an initial state is an execution in which no process has yet taken a step
- the execution consists of only inputs for each process
Proof of Lemma 2
Must show: there is a bivalent initial state
Argument:
- by contradiction: suppose no bivalent initial state
- consider sequence of initial states
- show some are $0$-valent, some are $1$-valent
- show that some must be bivalent
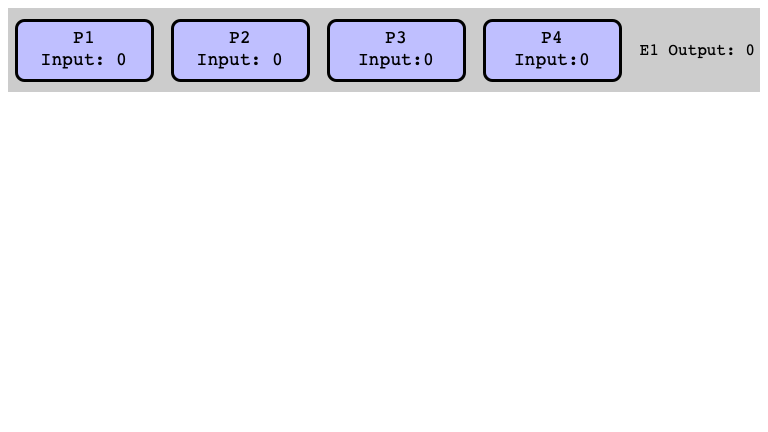
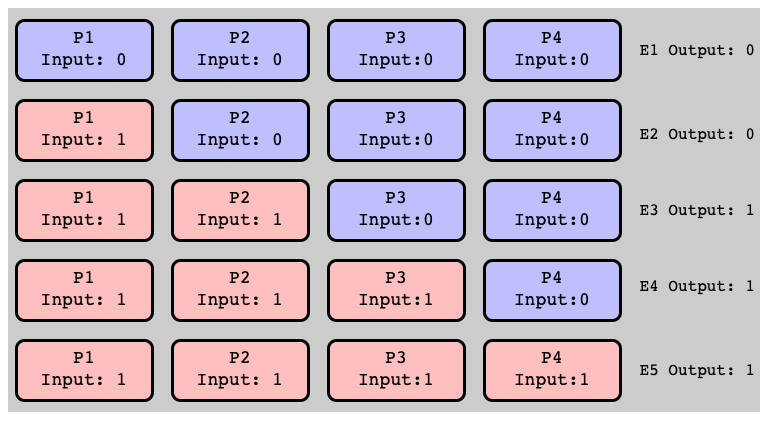
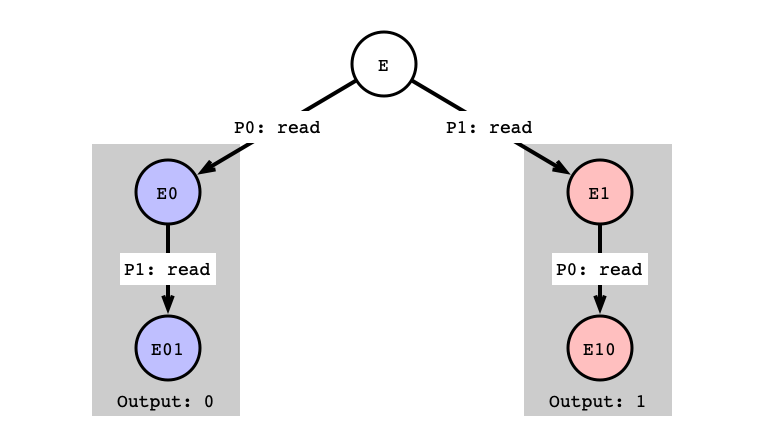
$E_1$ is $0$-valent (Why?)
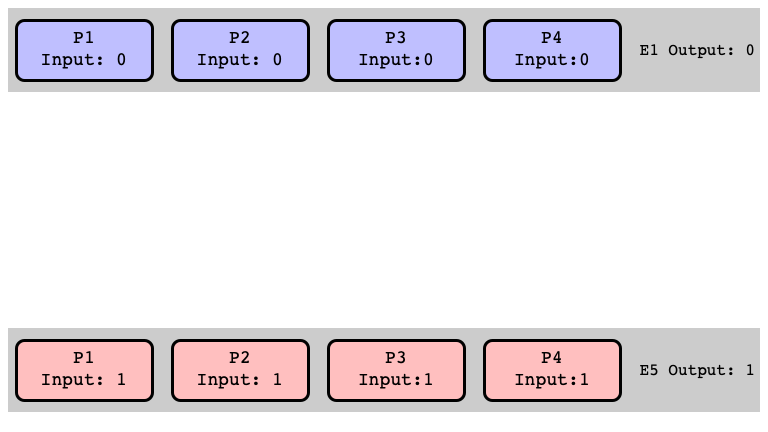
$E_5$ is $1$-valent
More Initial States
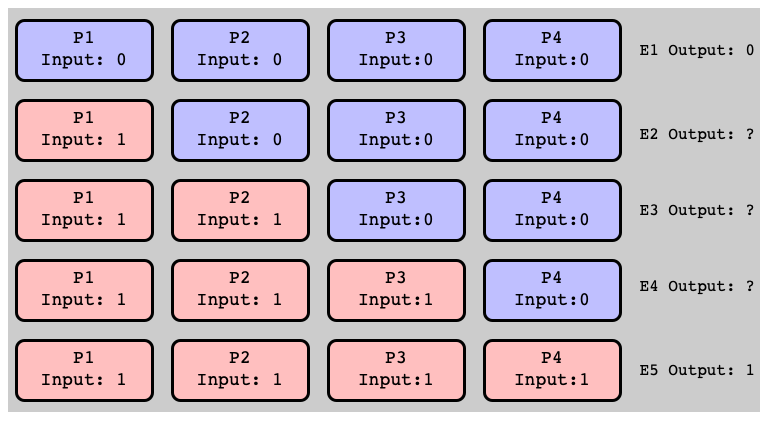
Assume: All Univalent
Adjacent Pair, Different Valency
All Extensions of $E_2$ Return $0$
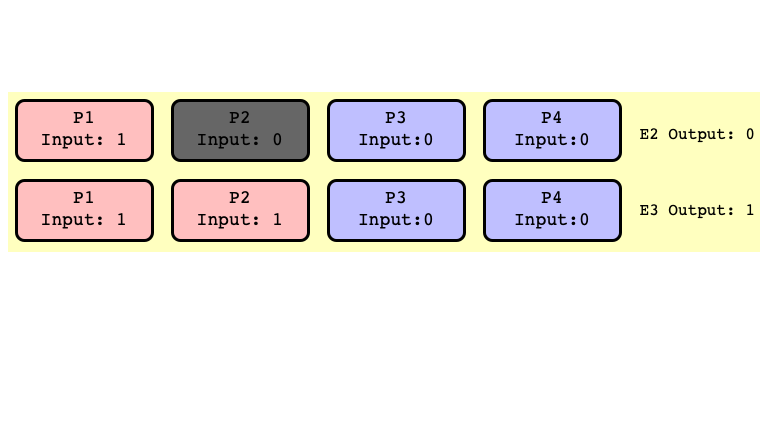
All Extensions of $E_3$ Return $1$
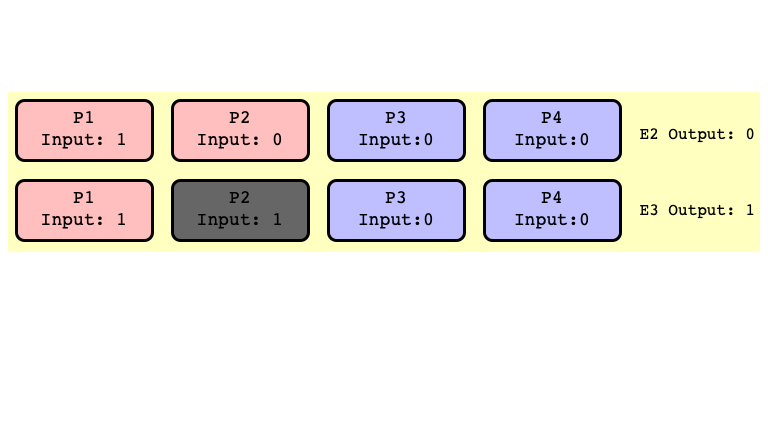
$E_2’$ and $E_3’$ Indistinguishable
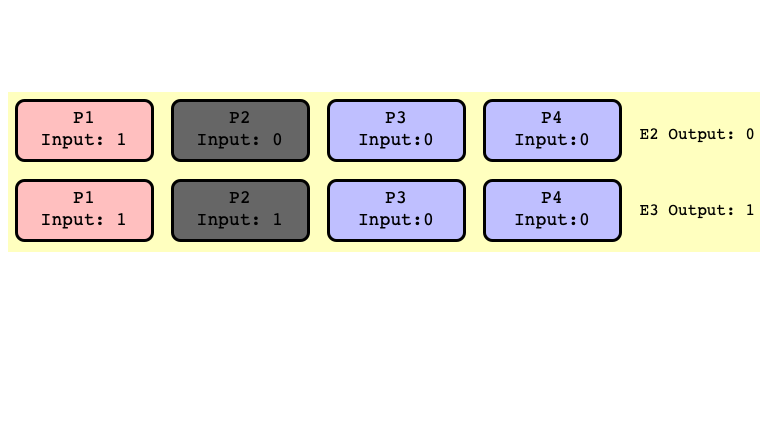
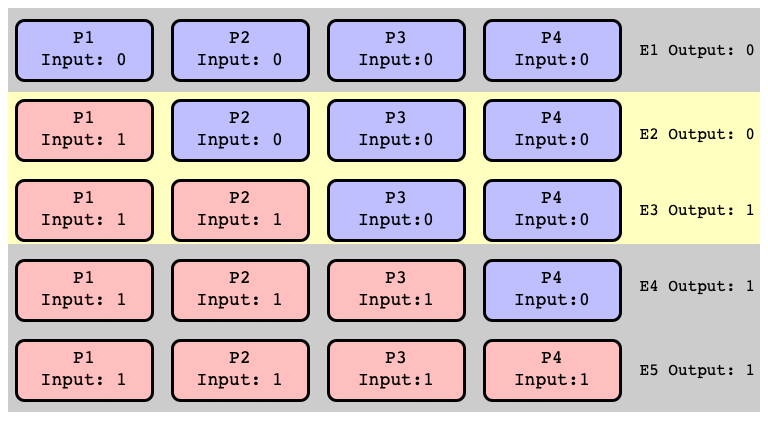
$E_2$ and $E_3$ Bivalent
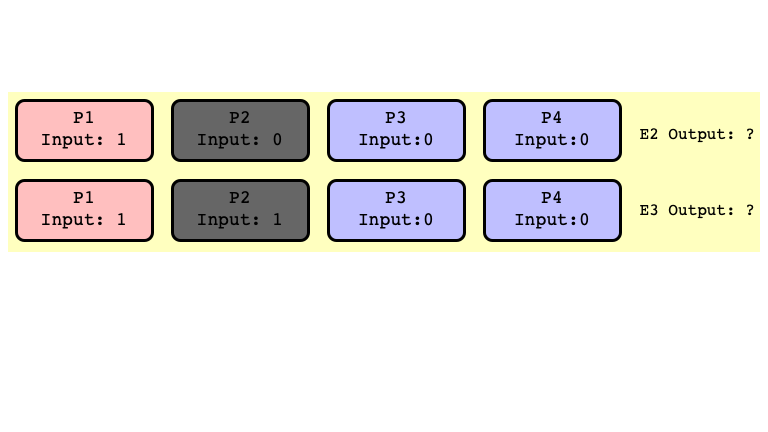
Note
Don’t need to assume $P_2$ crashes
- just assume first step of $P_2$ is scheduled after some other thread outputs
- this is possible because we assume $A$ is wait-free
- some process guaranteed to terminate even if one is not scheduled
Mere possibility of a crash together with wait-free assumption implies existence a bivalent initial state
- same holds if we require only termination with one fault
Critical Executions
An execution $E$ is critical if:
- $E$ is bivalent
- Extending $E$ by any single step of any process results in a univalent execution
Important Obvservation 3
Lemma 3. Every consensus protocol has a critical execution.
Proof of Lemma 3
Consider a bivalent initial state $E_0$
- Why does such a state exist?
-
If $E_0$ is critical, we’re done
-
What if $E_0$ is not critical?
- form $E_0, E_1, E_2, \ldots$ where
- each $E_{i+1}$ extends $E_i$ by single step
- each $E_i$ is bivalent
-
By wait-freedom, the sequence must be finite
- So it has a final $E$ where every extension is univalent
- $E$ is critical!
Properties of Consensus
Lemma 2. Every consensus protocol has a bivalent initial state.
Lemma 3. Every consensus protocol has a citical execution $E$.
So far: Have not used any properties of atomic read/write registers
- These properties hold for all consensus protocols
- even if other atomic operations are supported
Outline of Proof of FLP
Assume only 2 processes, $P_0$ and $P_1$
- Start from a critical execution $E$
- $E$ is bivalent, but any extension is univalent
- Consider all possibilities for next step:
- both threads
readfor next step - one thread
reads, the otherwrites - both threads
write
- both threads
- Show that in any case, we contradict either criticality of
Eor correctness of protocol
Assumptions
Without loss of generality:
- There are two processes $P_0$ and $P_1$
- $E$ is a critical state
- if $P_0$ has next step, resulting execution is $0$-valent
- if $P_1$ has next step, resulting execution is $1$-valent
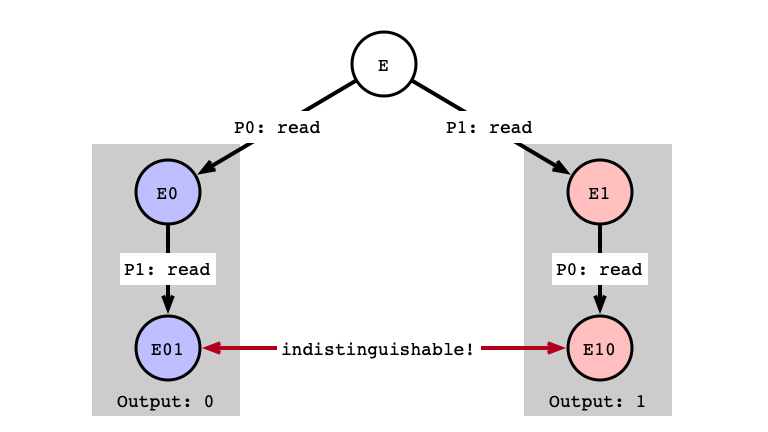
Case 1: read/read
Assumption: next operations for both $P_0$ and $P_1$ are read
- Start from critical state $E$
- if $P_0$ steps next, output is
0 - if $P_1$ steps next, output is
1
- if $P_0$ steps next, output is
read/read
read/read Next Step
read/read Problem
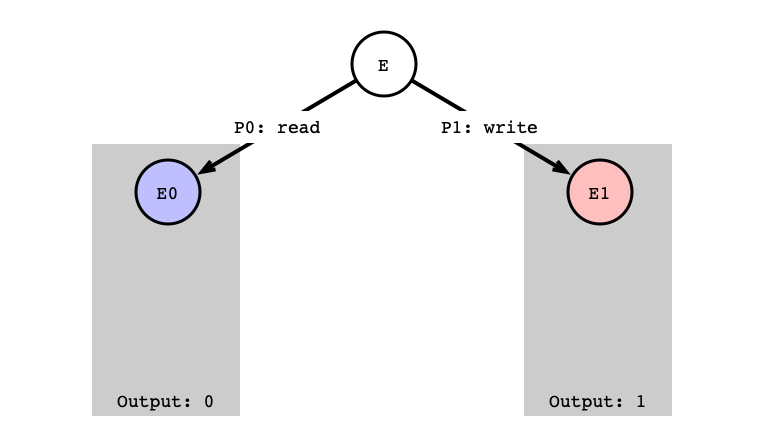
Case 2: read/write
Assumption:
- $P_0$’s next step is
read -
$P_1$’s next step is
write - Start from critical state $E$
- if $P_0$’s
readstep is next, output is0 - if $P_1$’s
writestep is next, output is1
- if $P_0$’s
read/write Setup
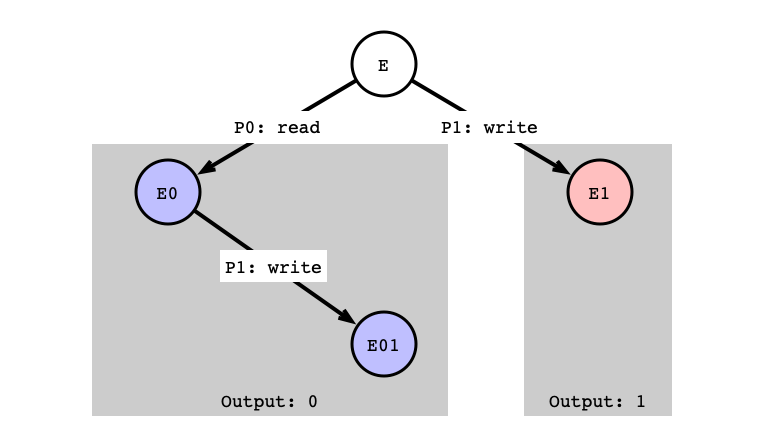
read/write Next Step
read/write Indistinguishable
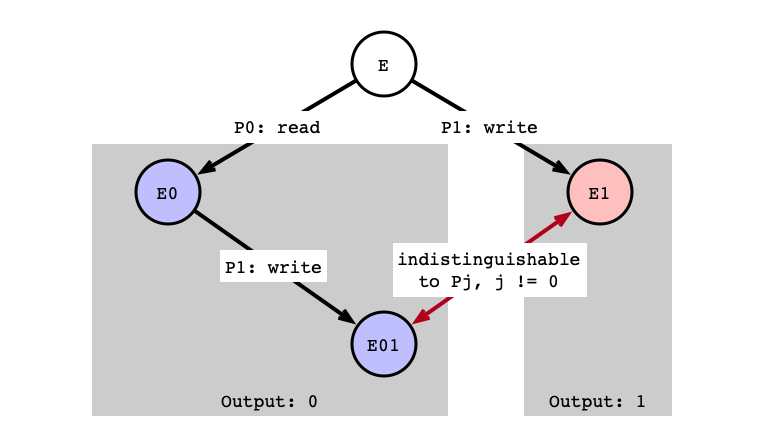
read/write $P_0$ Crashes

Case 3: write/write
Assumption: next operation for both $P_0$ and $P_1$ is write
Subcases:
- Sub-case a: write to different registers
- Sub-case b: write to same register
write/write Different Registers
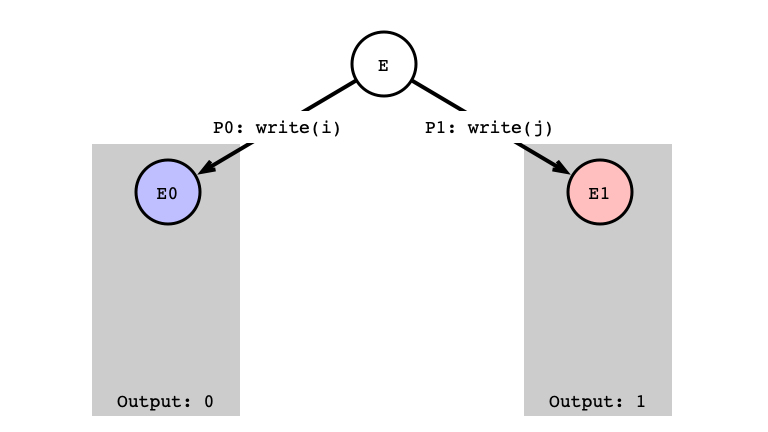
write/write Next Step
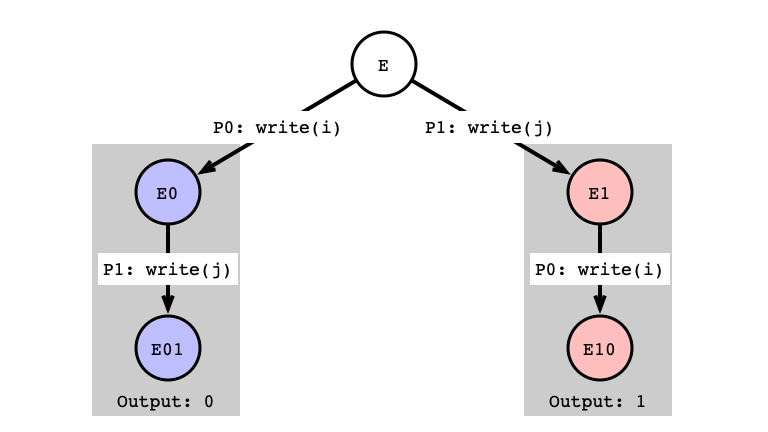
write/write Indistinguishable
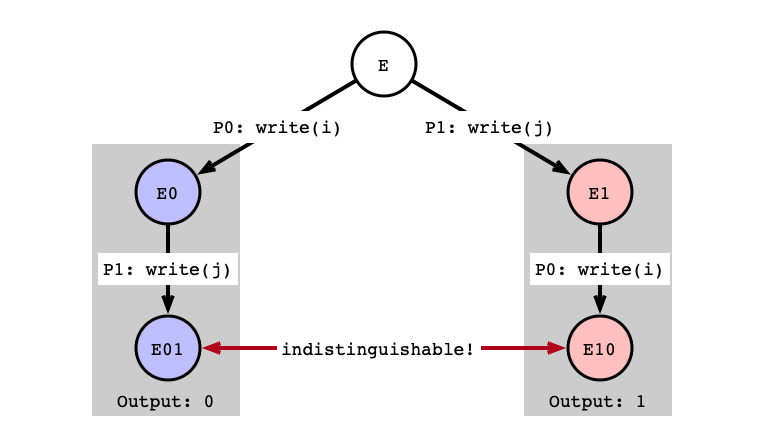
write/write Same Register
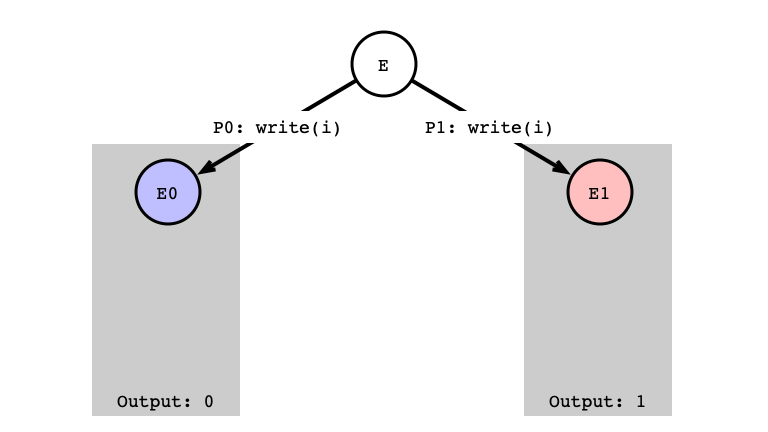
write/write Next Step
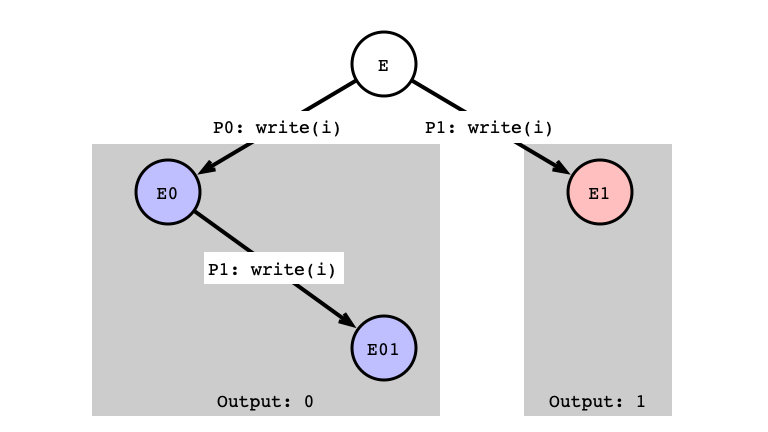
write/write Indistinguishable
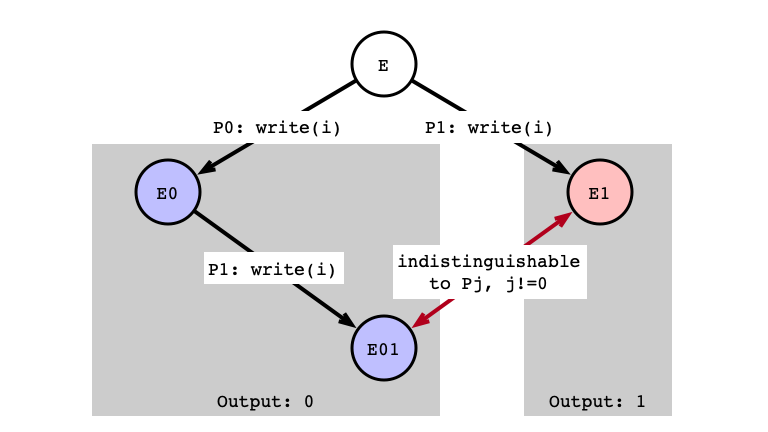
Conclusion
In general:
- Indistinguishable executions produce same output
Assuming a wait-free consensus protocol using only read/write registers:
- Showed there is a bivalent initial state
- Showed there is a critical execution
- Given a critical execution
- found indistinguishable states that must give different outputs
- this is a contradiction!
Remark. 1 and 2 hold for all protocols; 3 assumes only read/write registers