Lecture 31: Optimistic Linked Lists

COSC 273: Parallel and Distributed Computing

Spring 2023

Annoucements

1. Leaderboard submission results tomorrow
2. Next leaderboard submission is Friday? Monday?
3. Take-home quiz: released Wednesday (Gradescope), due Friday
   • concurrent linked lists

Today

Concurrent Linked Lists, Three Ways:

1. Coarse locking
2. Fine-grained locking
3. Optimistic locking

A Generic Task

Store, access, & modify collection of distinct elements:

The Set ADT:

• add an element
  • no effect if element already there
• remove an element
  • no effect if not present
• check if set contains an element

Java SimpleSet Interface

public interface SimpleSet<T> {
// Add an element to the SimpleSet. Returns true if the element
// was not already in the set.
boolean add(T x);

// Remove an element from the SimpleSet. Returns true if the
// element was previously in the set.
boolean remove(T x);

// Test if a given element is contained in the set.
boolean contains(T x);
}

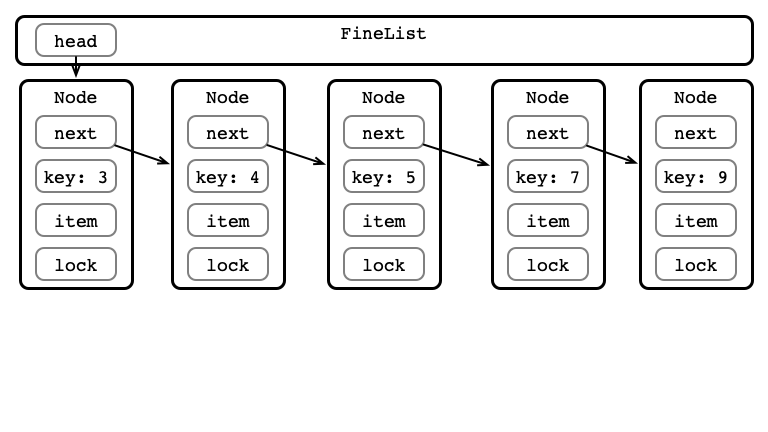
Linked List SimpleSets

• Each Node stores:
  • reference to the stored object
  • reference to the next Node
  • a numerical key associated with the object
• The list stores
  • reference to head node
  • a tail node
  • head and tail have min and max key values
  • nodes have strictly increasing keys

Why Keys?

Question. Why is it helpful to store keys in increasing order?

Our Goals

1. Correctness, safety, liveness
   • deadlock-freedom
   • starvation-freedom?
   • nonblocking??
   • linearizability???
2. Performance
   • parallelism?

Synchronization Philosophies

1. Coarse-Grained (CoarseList.java)
   • lock whole data structure for every operation
2. Fine-Grained (FineList.java)
   • only lock what is needed to avoid disaster
3. Optimistic (OptimisticList.java)
   • don’t lock anything to read, only lock to modify
4. Lazy (LazyList.java)
   • use “logical” removal, only lock occasionally
5. Nonblocking (NonblockingList.java)
   • use atomics, not locks!

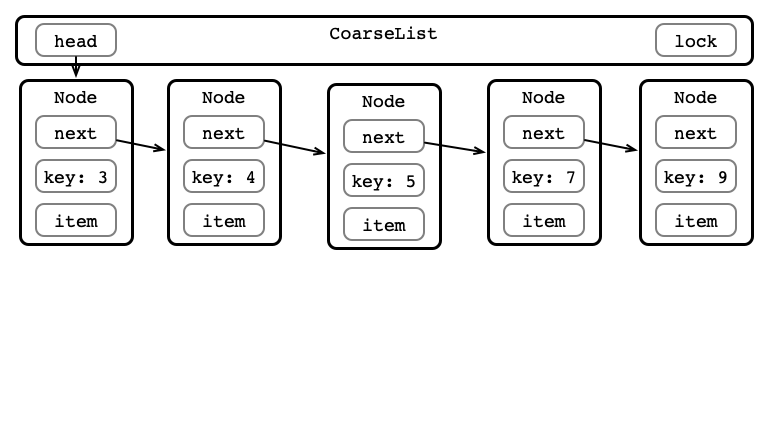
Coarse-grained Locking

One lock for whole data structure

For any operation:

1. Lock entire list
2. Perform operation
3. Unlock list

See CoarseList.java

Coarse-grained Insertion

Step 1: Acquire Lock

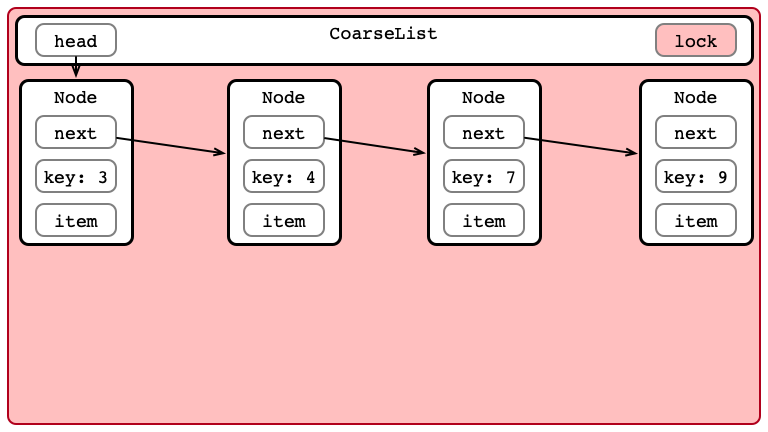
Step 2: Iterate to Find Location

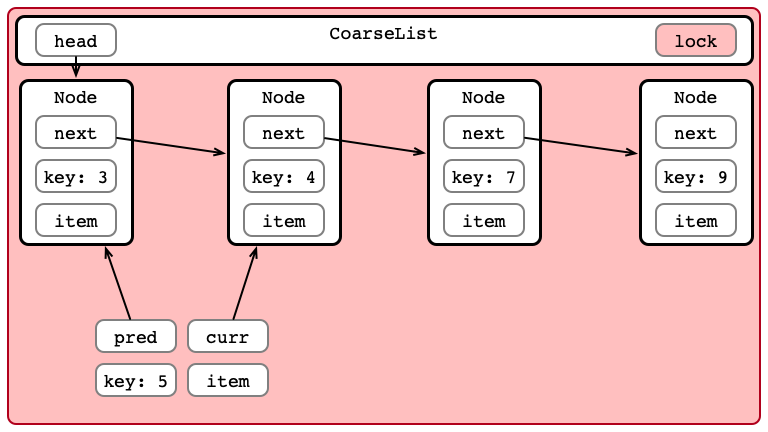
Step 2: Iterate to Find Location

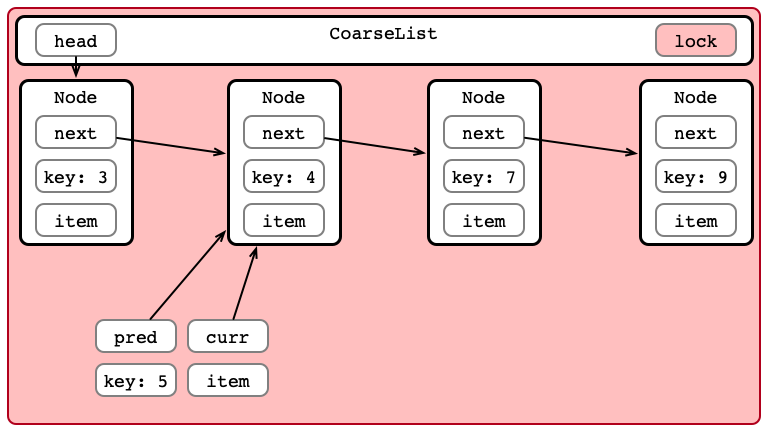
Step 2: Iterate to Find Location

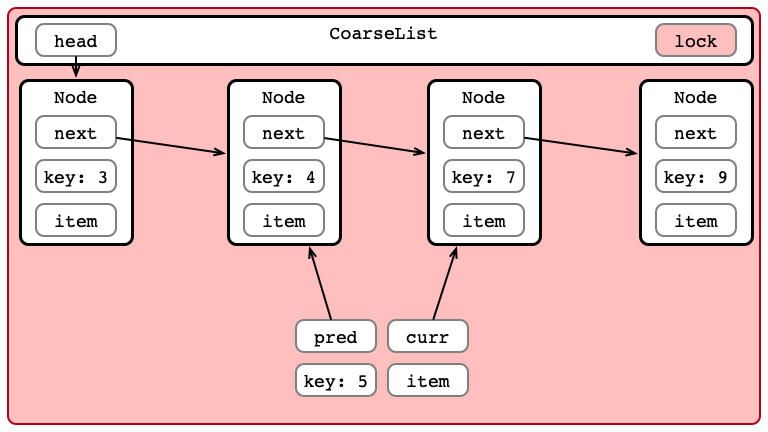
Step 3: Insert Item

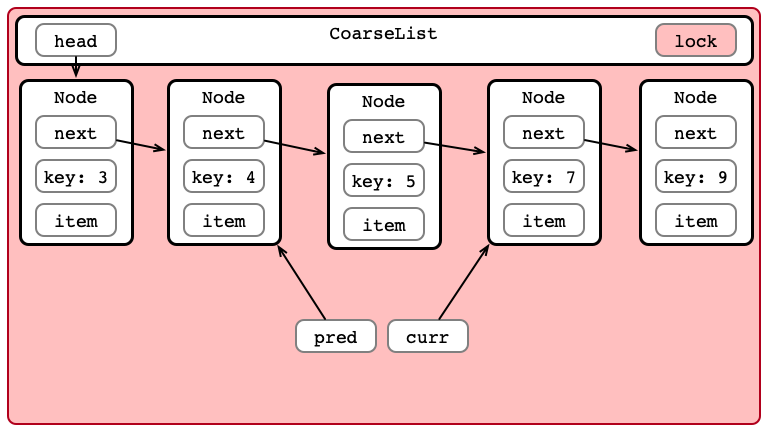
Step 4: Unlock List

Coarse-grained Appraisal

Advantages:

• Easy to reason about
• Easy to implement

Disadvantages:

• No parallelism
• All operations are blocking

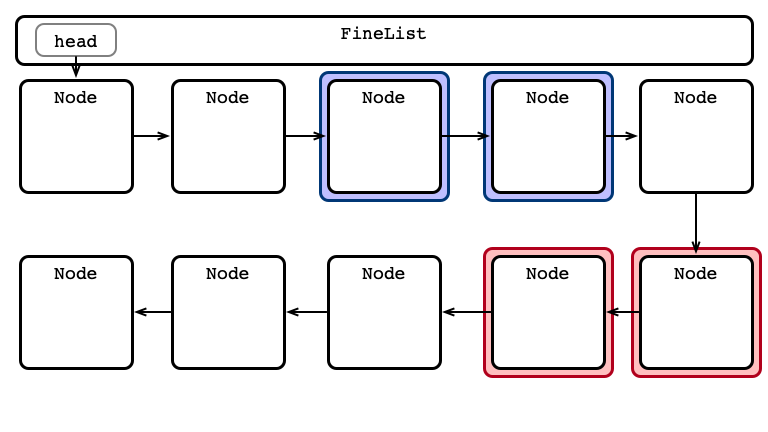
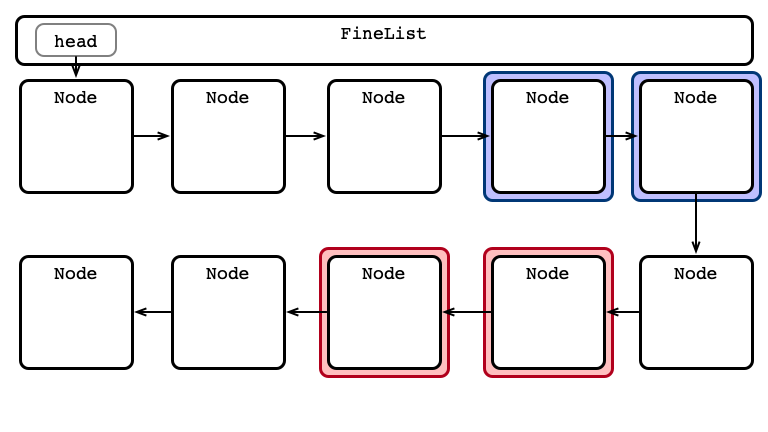
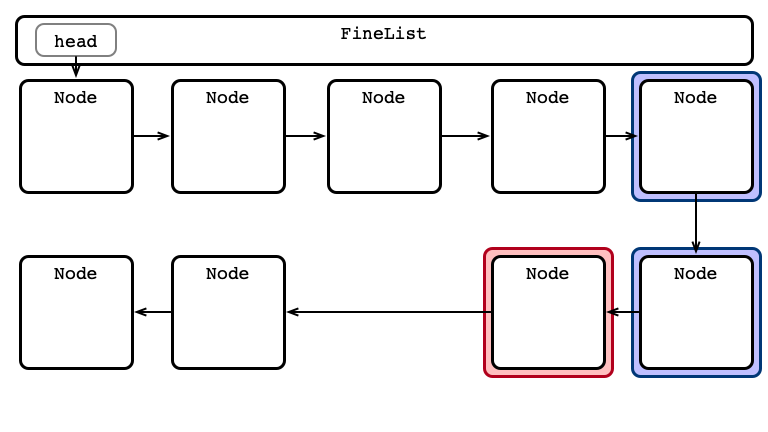
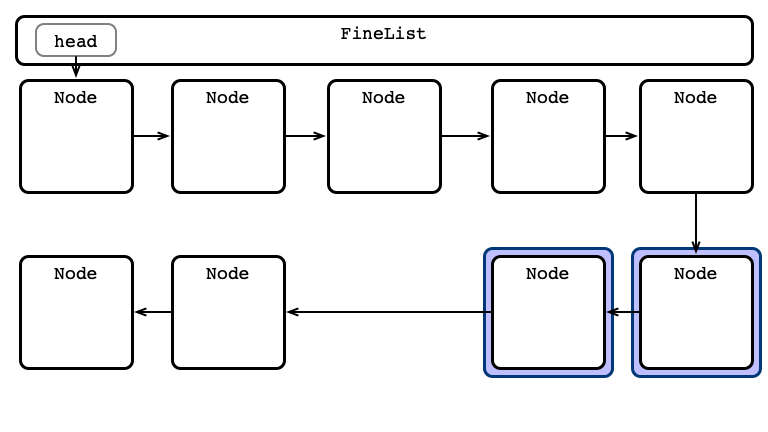
Fine-grained Locking

One lock per node

For any operation:

1. Lock head and its next
2. Hand-over-hand locking while searching
   • always hold at least one lock
3. Perform operation
4. Release locks

See FineList.java

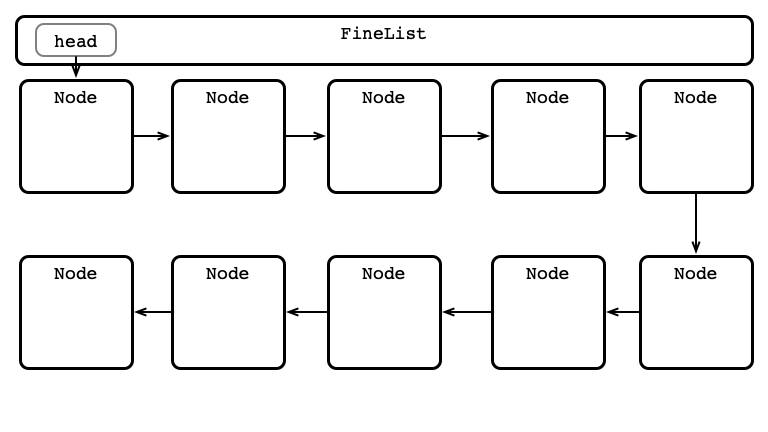
A Fine-grained Insertion

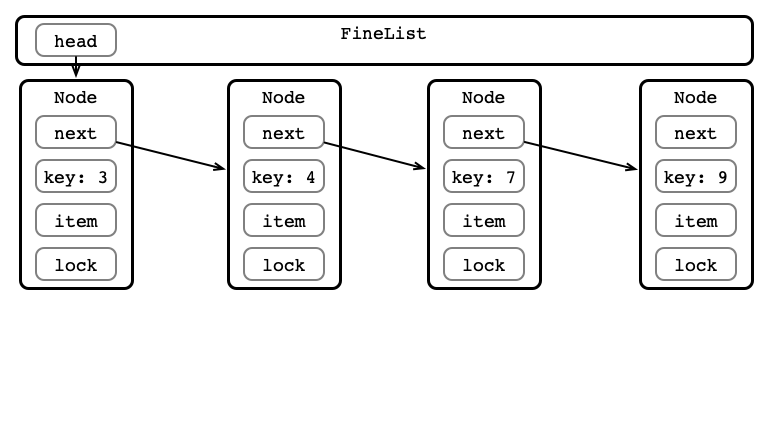
Step 1: Lock Initial Nodes

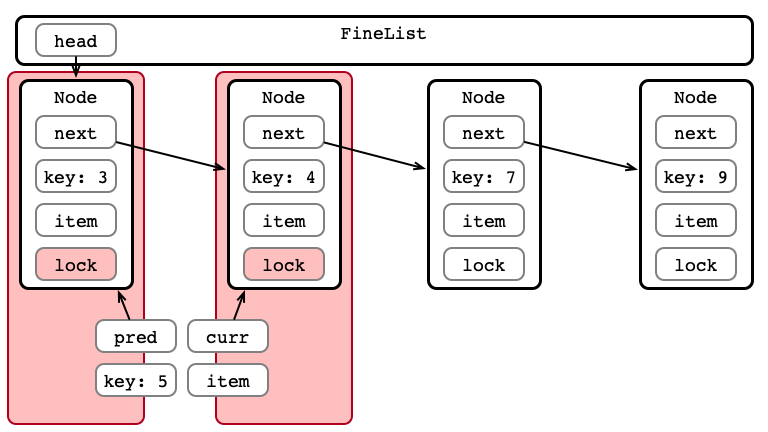
Step 2: Hand-over-hand Locking

Step 2: Hand-over-hand Locking

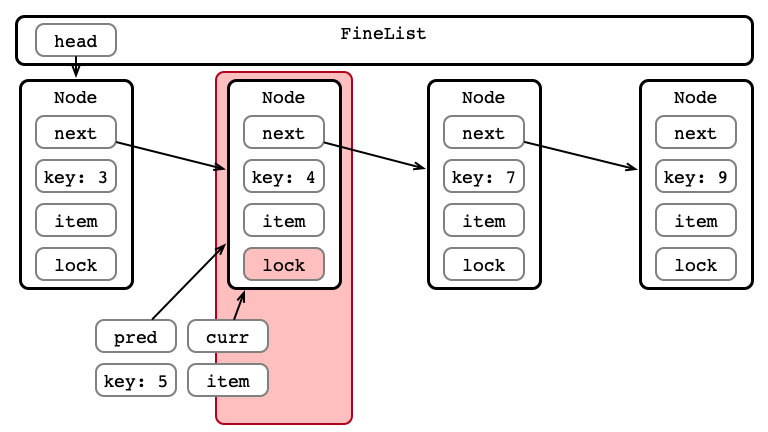
Step 2: Hand-over-hand Locking

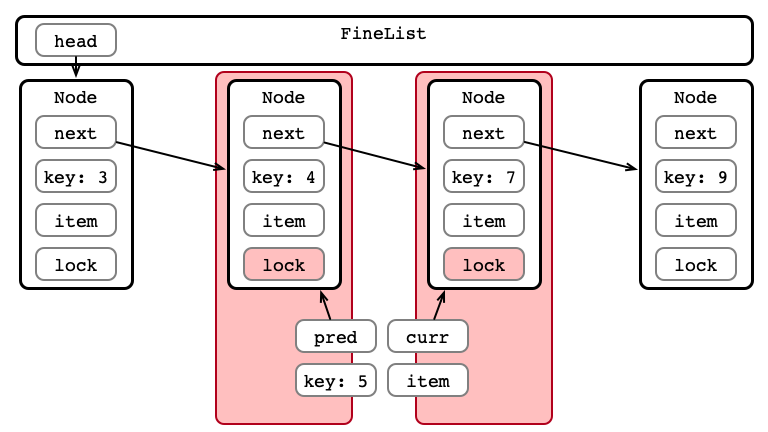
Step 3: Perform Insertion

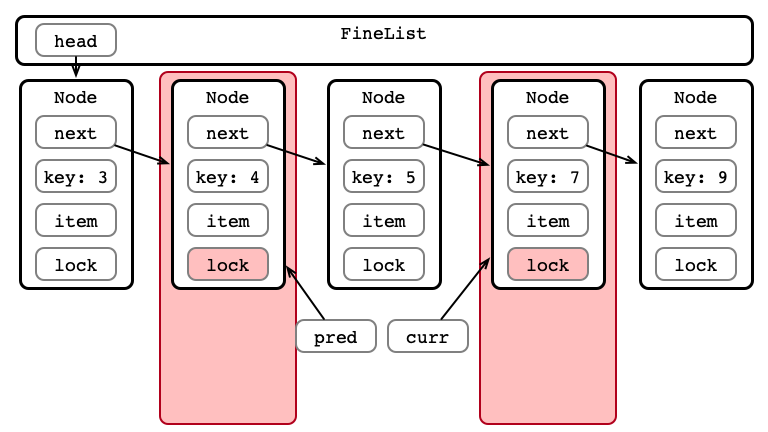
Step 4: Unlock Nodes

An Advantage: Parallel Access

An Advantage: Parallel Access

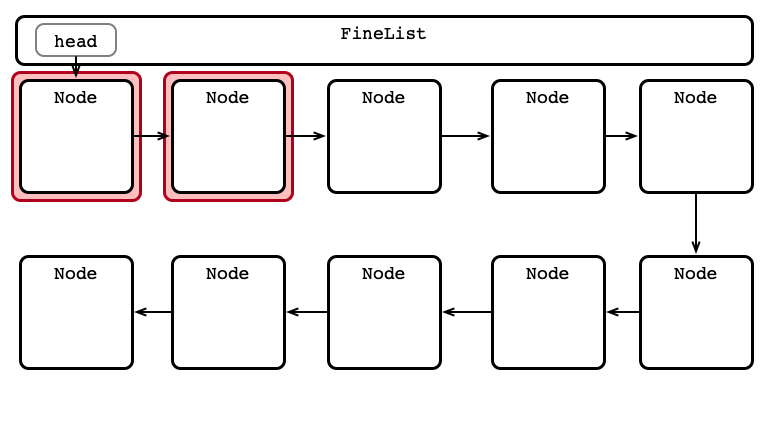
An Advantage: Parallel Access

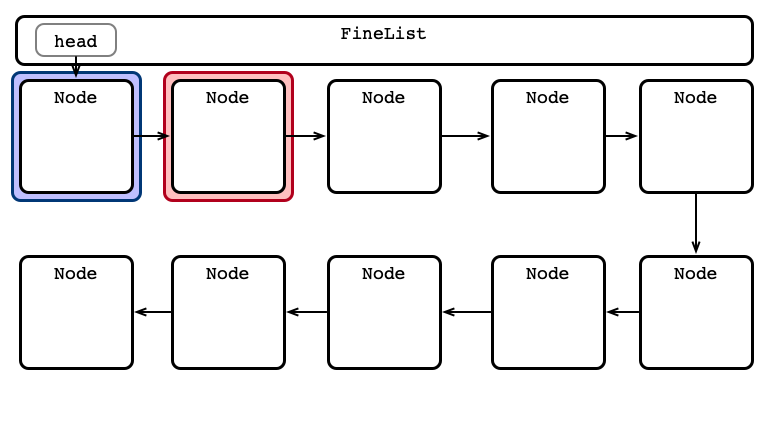
An Advantage: Parallel Access

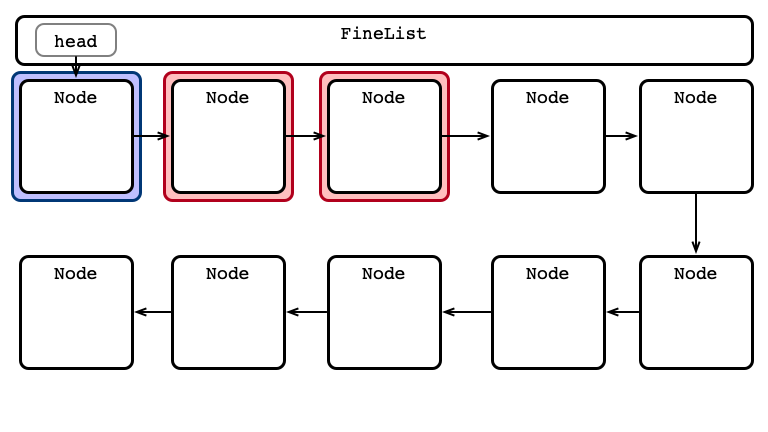
An Advantage: Parallel Access

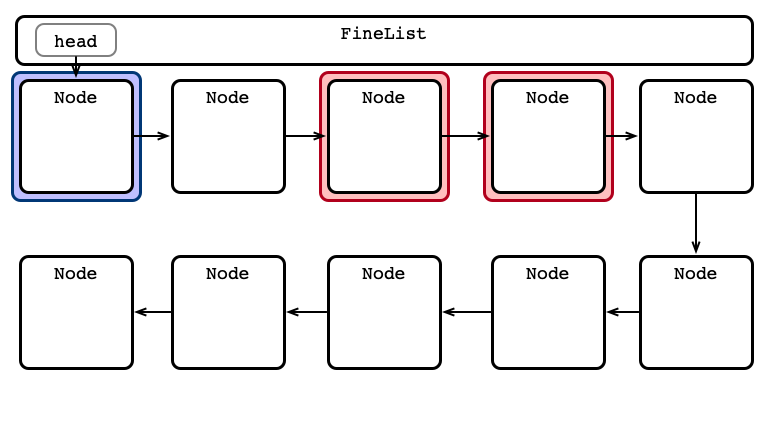
An Advantage: Parallel Access

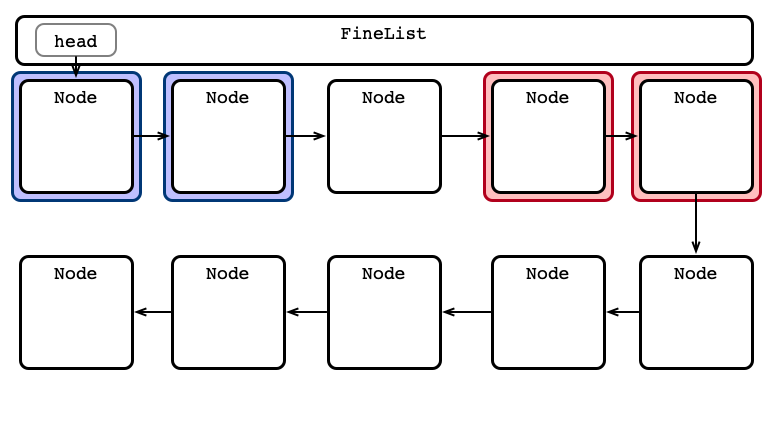
An Advantage: Parallel Access

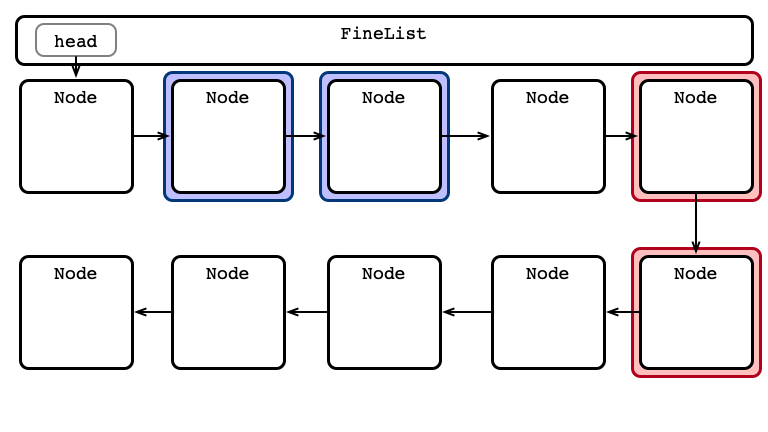
An Advantage: Parallel Access

An Advantage: Parallel Access

An Advantage: Parallel Access

An Advantage: Parallel Access

An Advantage: Parallel Access

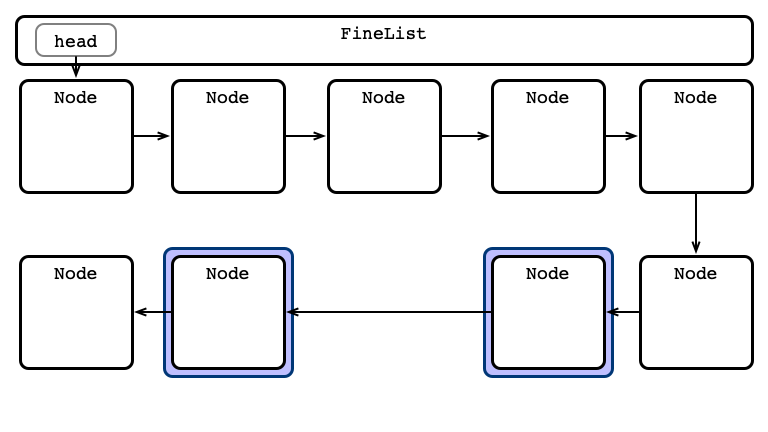
Fine-grained Appraisal

Advantages:

• Parallel access
• Reasonably simple implementation

Disadvantages:

• More locking overhead
  • can be much slower than coarse-grained
• All operations are blocking

Optimistic Synchronization

Fine-grained wastes resources locking

• Nodes are locked when traversed
• Locked even if not modified!

A better procedure?

1. Traverse without locking
2. Lock relevant nodes
3. Perform operation
4. Unlock nodes

A Better Way?

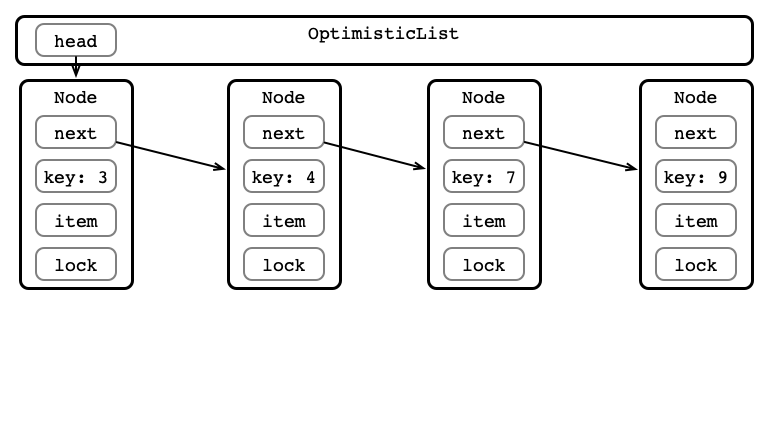
A Better Way?

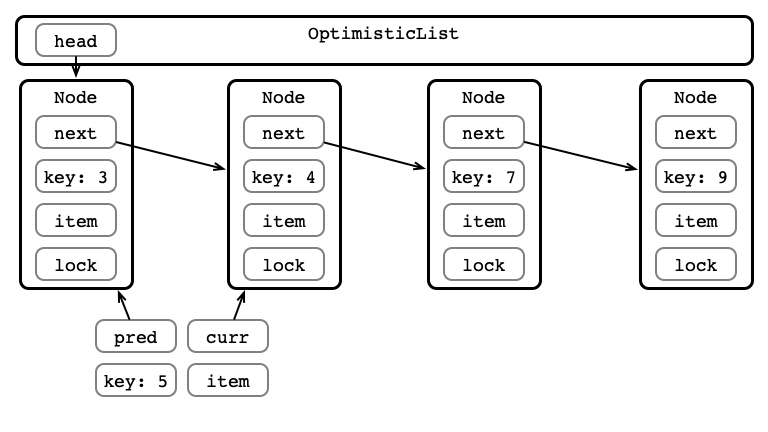
A Better Way?

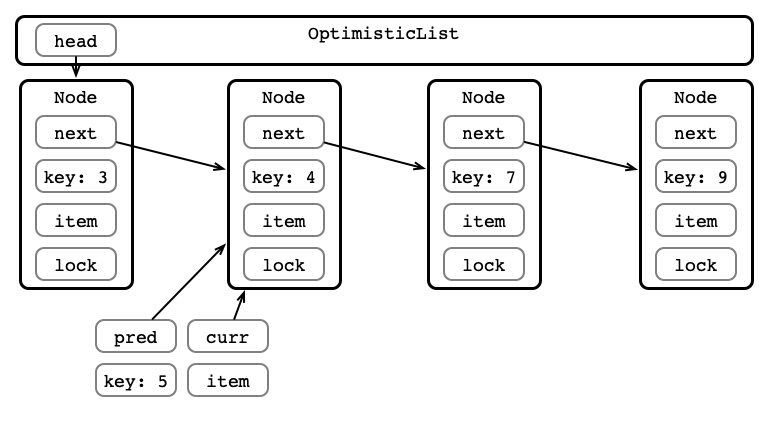
A Better Way?

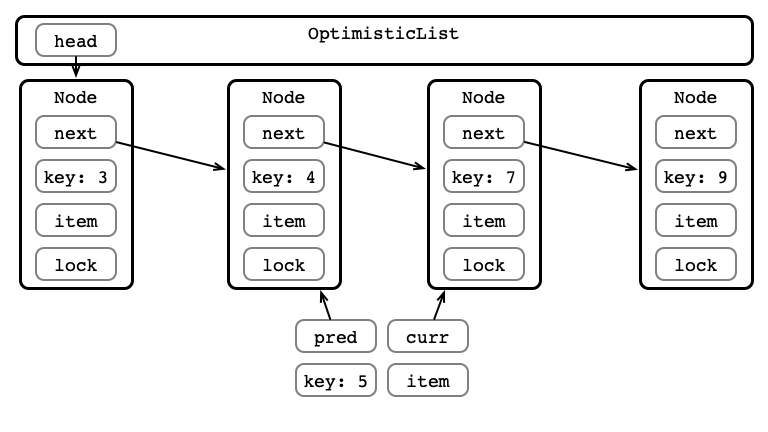
A Better Way?

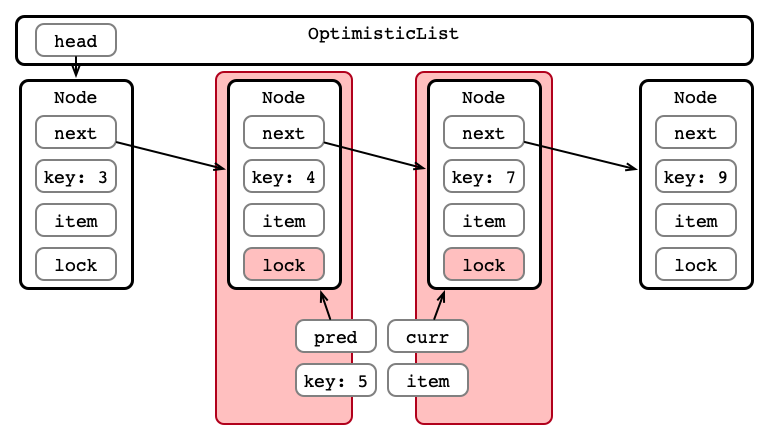
A Better Way?

What Could Go Wrong?

An Issue!

Between traversing and locking

• Another thread modifies the list
• Now locked nodes aren’t the right nodes!

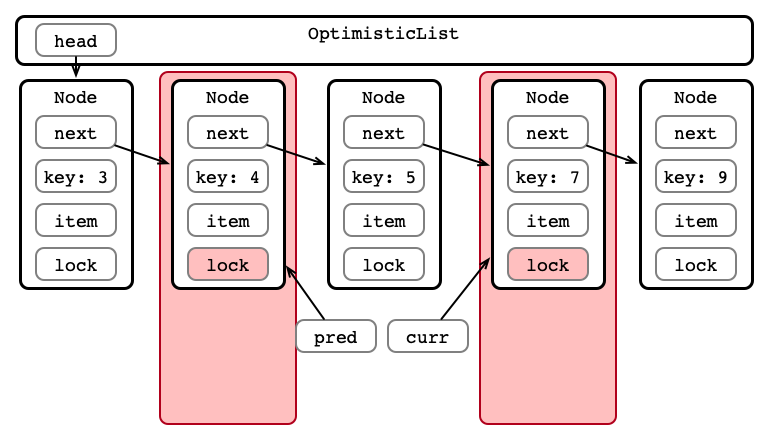
An Issue, Illustrated

An Issue, Illustrated

An Issue, Illustrated

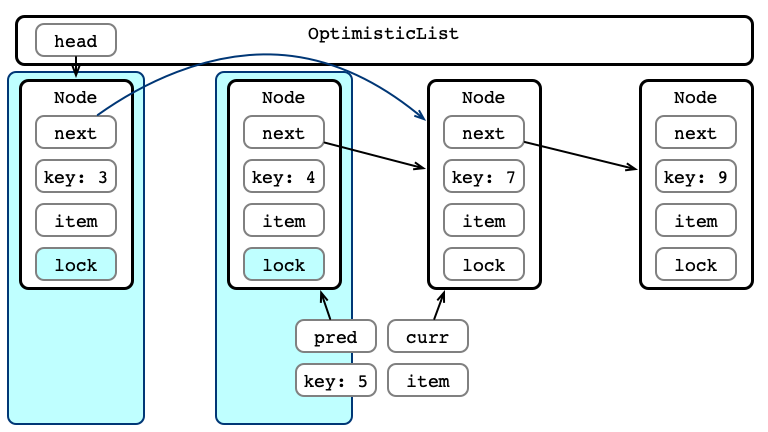
An Issue, Illustrated

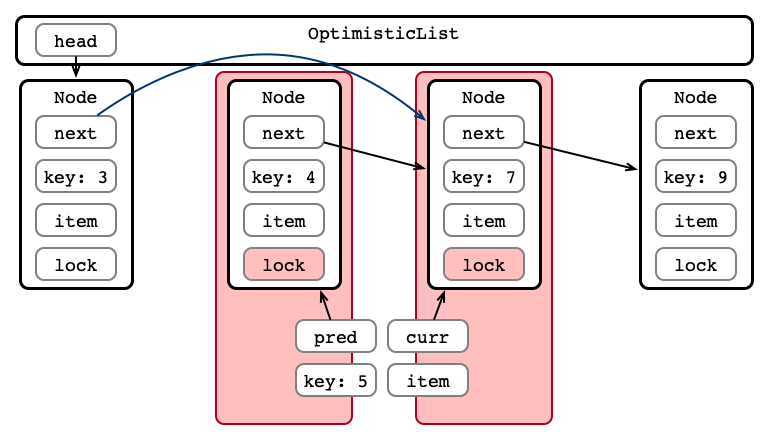
An Issue, Illustrated

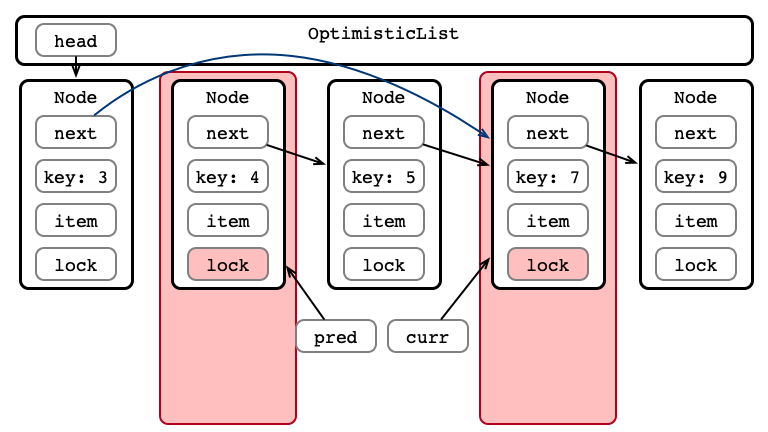
An Issue, Illustrated

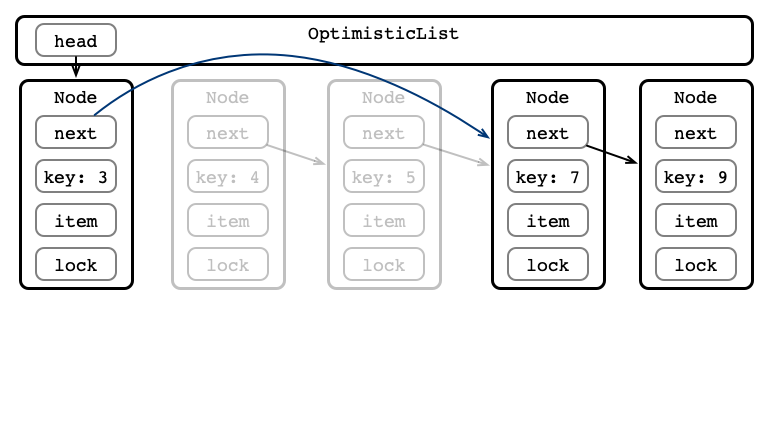
How can we Address this Issue?

Optimistic Synchronization, Validated

1. Traverse without locking
2. Lock relevant nodes
3. Validate list
   • if validation fails, go back to Step 1
4. Perform operation
5. Unlock nodes

Seet OptimisticList.java

How do we Validate?

After locking, ensure that:

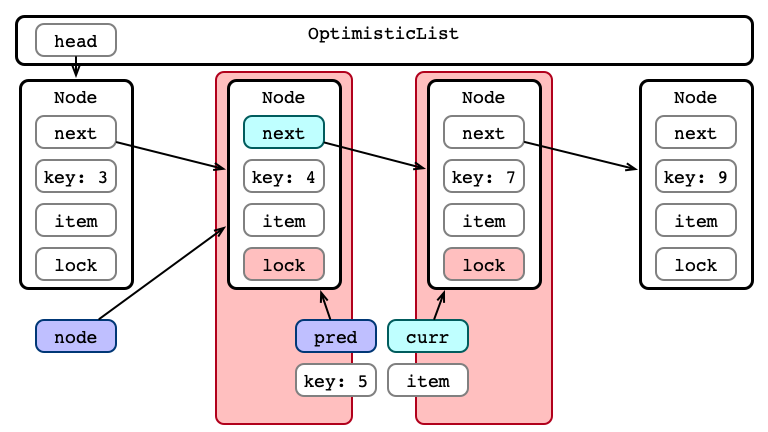
1. pred is reachable from head
2. curr is pred’s successor

If these conditions aren’t met:

• Start over!

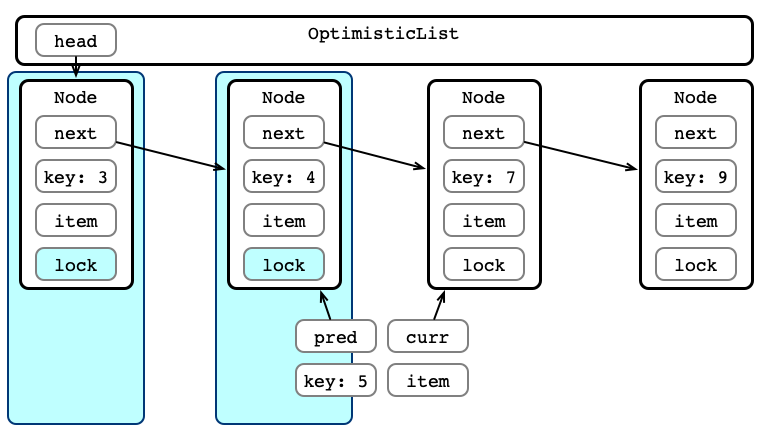
Optimistic Insertion

Step 1: Traverse the List

Step 1: Traverse the List

Step 1: Traverse the List

Step 2: Acquire Locks

Step 3: Validate List - Traverse

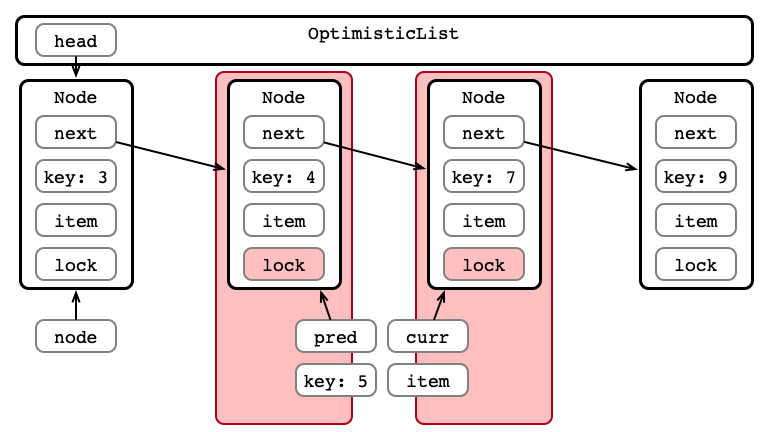
Step 3: Validate List - pred Reachable?

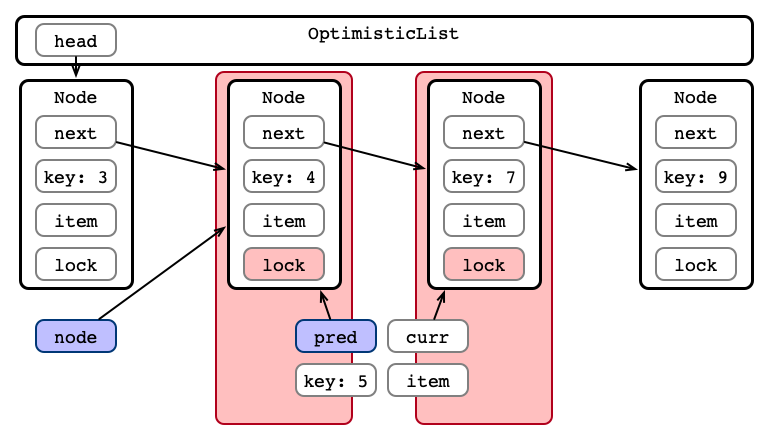
Step 3: Validate List - Is curr next?

Step 4: Perform Insertion

Step 5: Release Locks

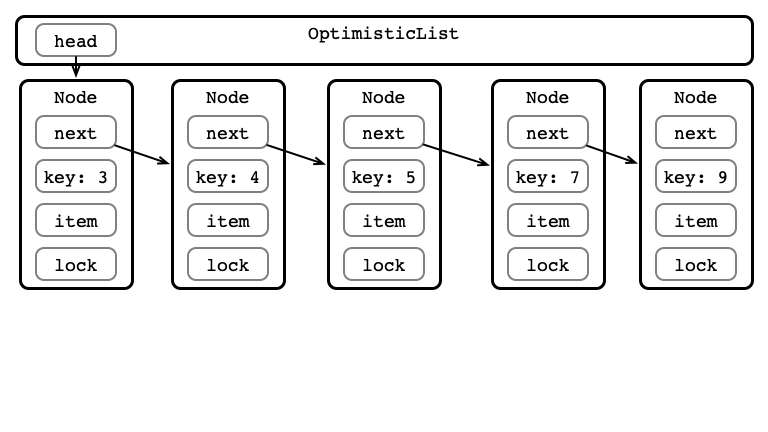
Implementing Validation

    private boolean validate (Node pred, Node curr) {
	Node node = head;
	while (node.key <= pred.key) {
	    if (node == pred) {
		return pred.next == curr;
	    }
	    node = node.next;
	}
	return false;
    }

Optimistic Appraisal

Advantages:

• Less locking than fine-grained
• More opportunities for parallelism than coarse-grained

Disadvantages:

• Validation could fail
• Not starvation-free
  • even if locks are starvation-free

Performance Tests

On HPC Cluster:

• Compare running times of performing 1M operations
  • add/remove/contains sequence chosen at random
  • elements chosen from 1 to N at random
    • N is universe size
• Parameters
  • universe size $\approx$ set size
  • number of threads

See SetTester.java

Performance Predictions?

Under what conditions do you expect coarse/fine/optimistic strategies to be performant?

• Number of threads (1 to 128 on HPC)
• Set universe size (8 to 8,192)

Performance v. Size, 1 Thread

Performance v. Size, 128 Threads

Time v. Threads, 8 Elements

Time v. Threads, 8,192 Elements

Coarse Time v. Threads

Fine Time v. Threads

Optimistic Time v. Threads

Next Time

Another Way: Lazy Synchronization

• don’t modify the list unless you really have to