Lecture 30: Sorting Networks

COSC 273: Parallel and Distributed Computing

Spring 2023

Annoucements

Submission links today:

1. Final Project Leaderboard Submissions
2. Choose Your Own Adventure Baselines

Today

Sorting small arrays quickly

Insertion Sort, Revisited

for (int i = 1; i < data.length; ++i) {
    for (int j = i; j > 0; --j) {
        if (data[j-1] > data[j]) {
            swap(data, j-1, j)		
        }
    }
}

Appealing Features of Insertion Sort

for (int i = 1; i < data.length; ++i) {
    for (int j = i; j > 0; --j) {
        if (data[j-1] > data[j]) {
            swap(data, j-1, j)		
        }
    }
}

1. Only modifications are (adjacent) swaps
   • sorting is in place
2. Access pattern is independent of input
   • inputs always read/compared in same order
   • only difference between execution is outcomes of swaps

Comparators: Visualizing Swaps

        if (data[i] > data[j]) {
            swap(data, i, j)
        }

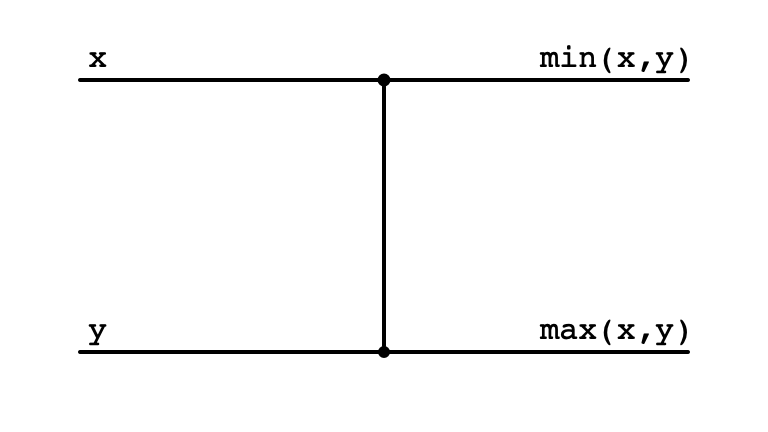
Comparator Swap

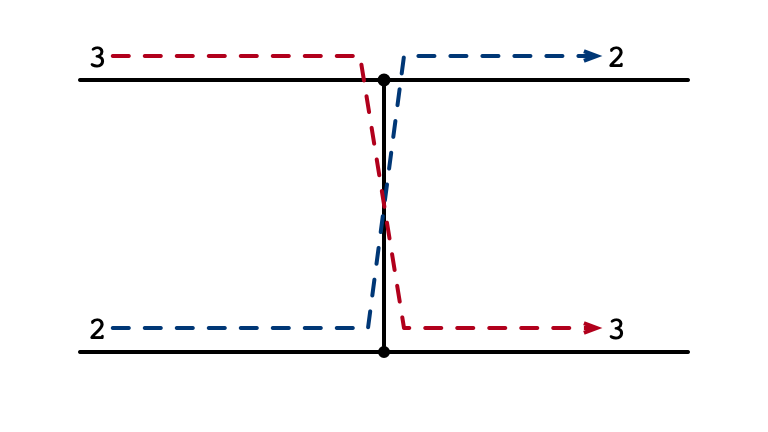
Comparator No Swap

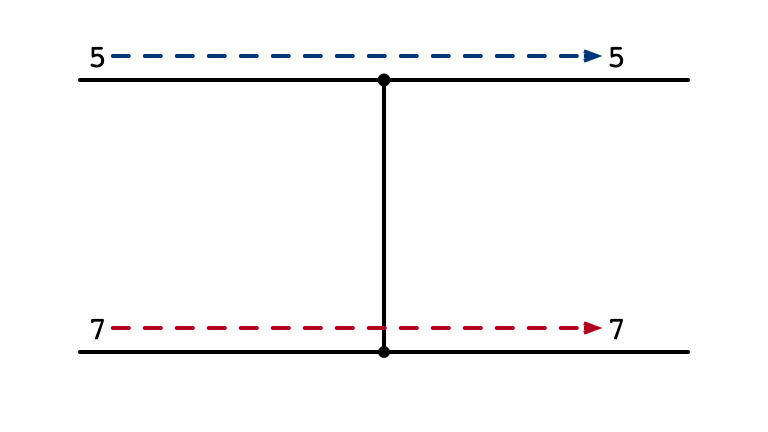
Sorting Array of Two Elements

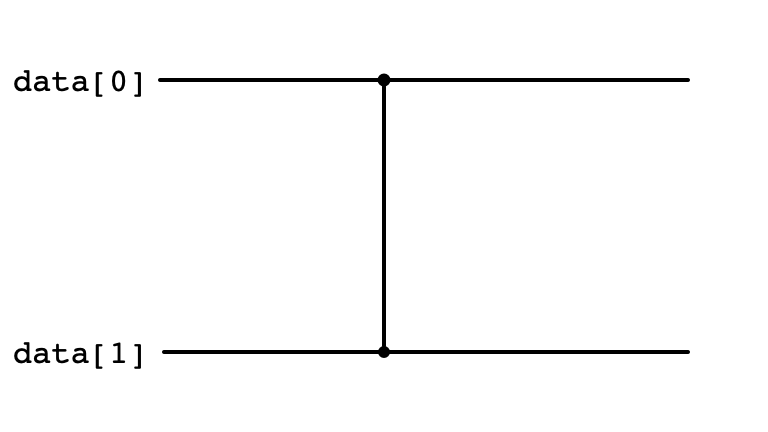
Insertion Sort

for (int i = 1; i < data.length; ++i) {
    for (int j = i; j > 0; --j) {
        if (data[j-1] > data[j]) {swap(data, j-1, j)}}}

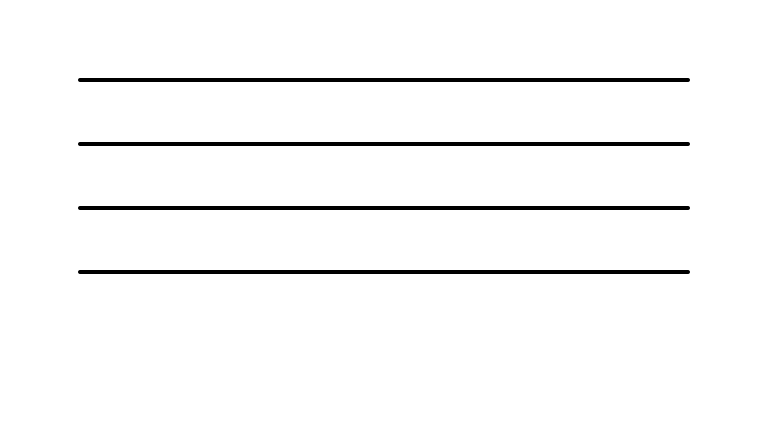
Insertion Sort: i = 1

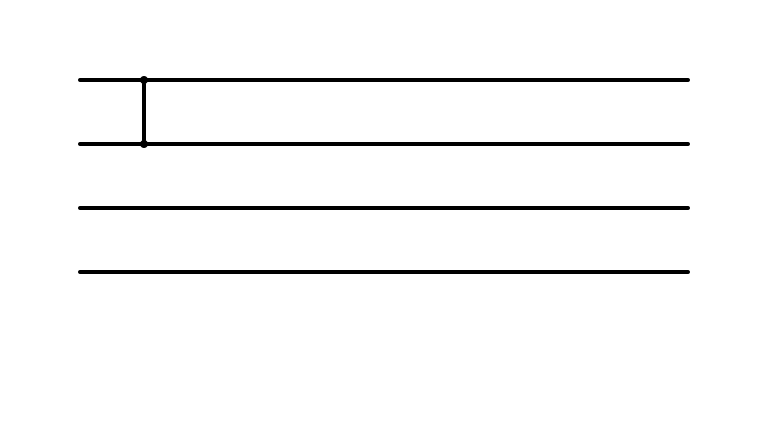
Insertion Sort: i = 2

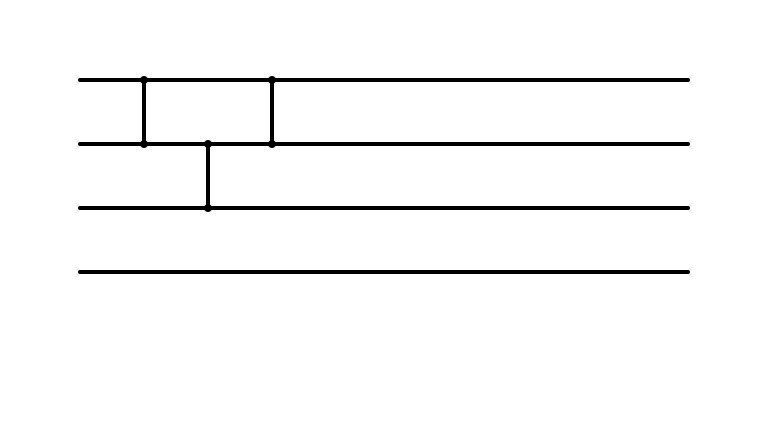
Insertion Sort: i = 3

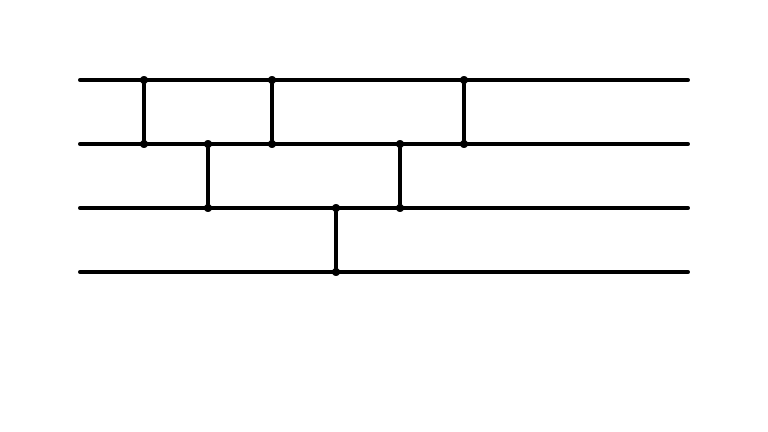
Which Operations can be Parallelized?

Parallelism

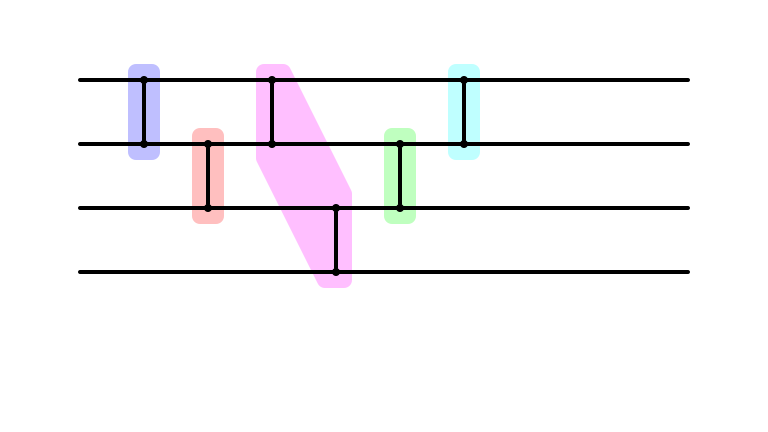
Cleaner Parallel Representation

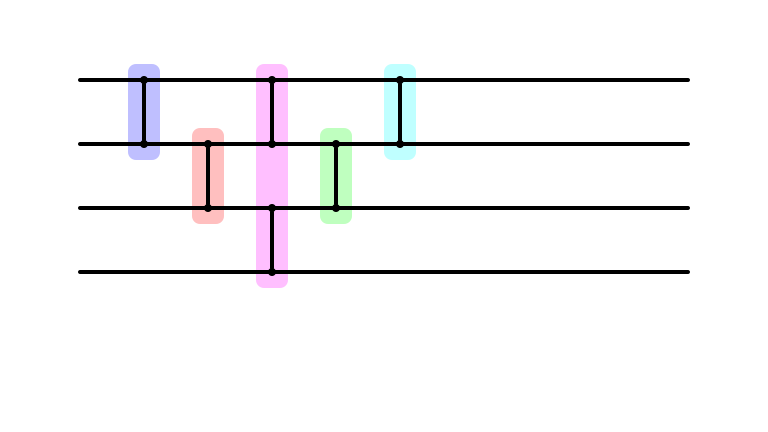
Depth

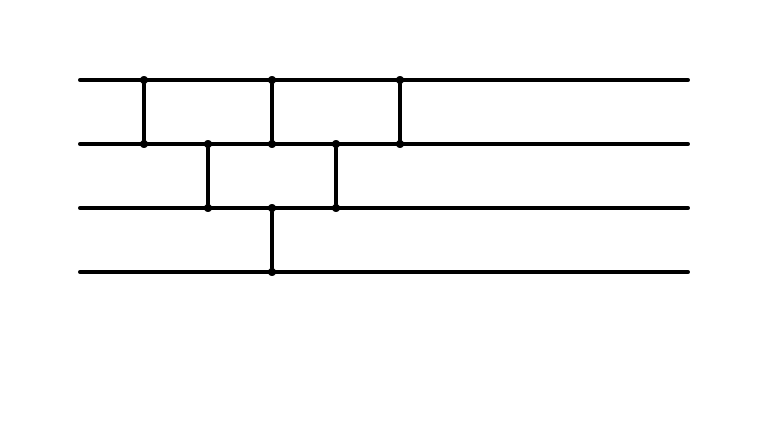
Insertion Sort: Larger Instance

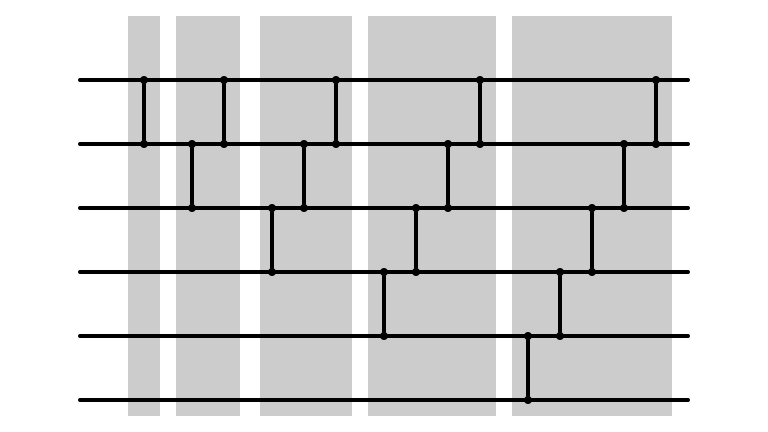
Done In Parallel?

Done In Parallel!

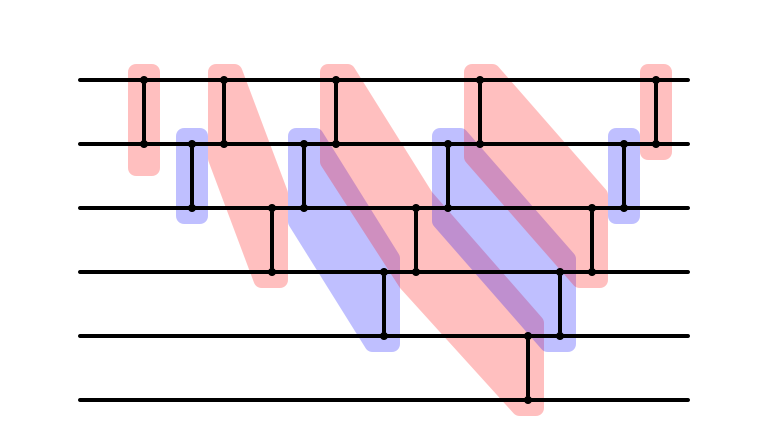
Cleaned Up

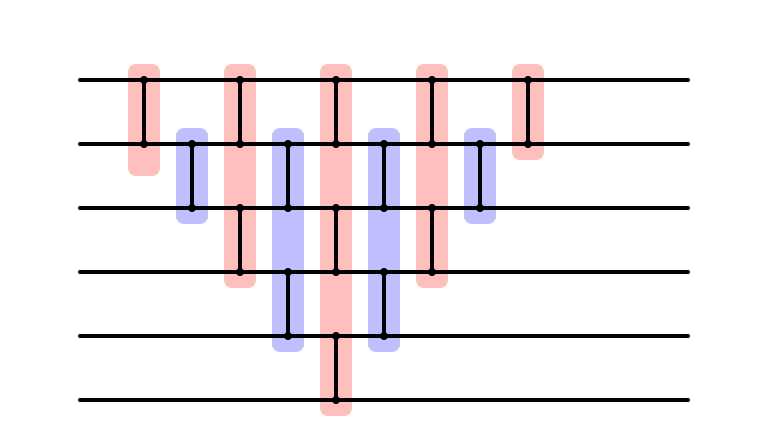
Parallel Depth?

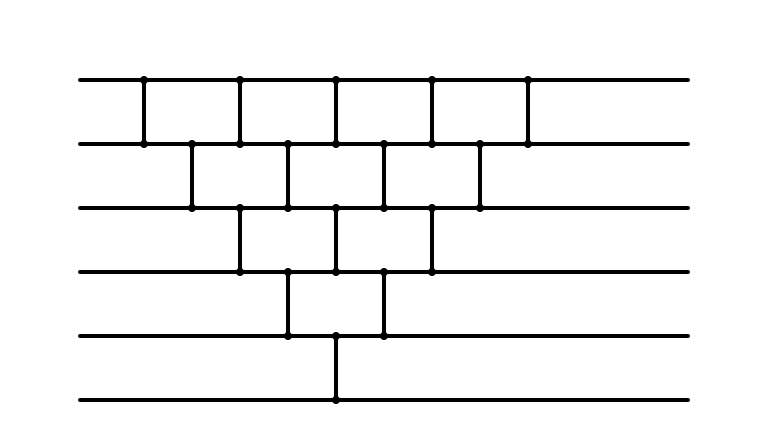
Bubble Sort

Consider:

for (int m = data.length - 1; m > 0; --m) {
    for (int i = 0; i < m; ++i) {
        if (data[i] > data[i+1]) {
            swap(data, i, i+1)		
        }
    }
}

Can we make a sorting network corresponding to bubble sort?

Bubble Sort: m = 6

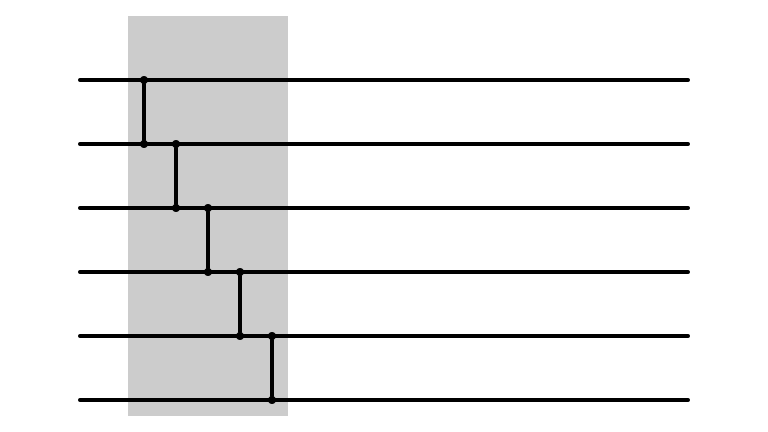
Bubble Sort: m = 5

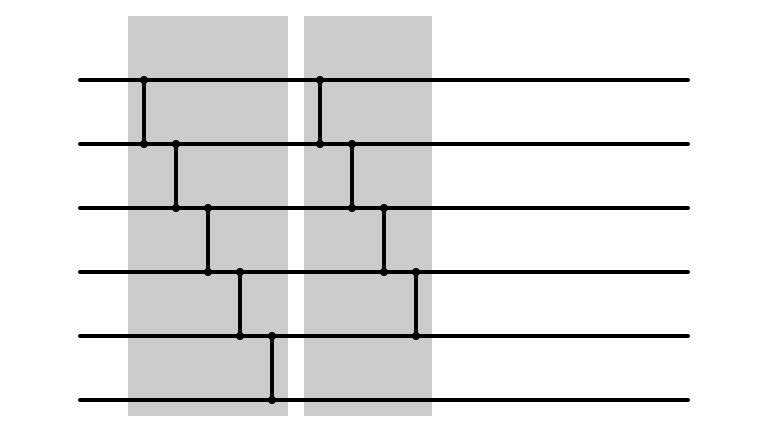
Bubble Sort: m = 4

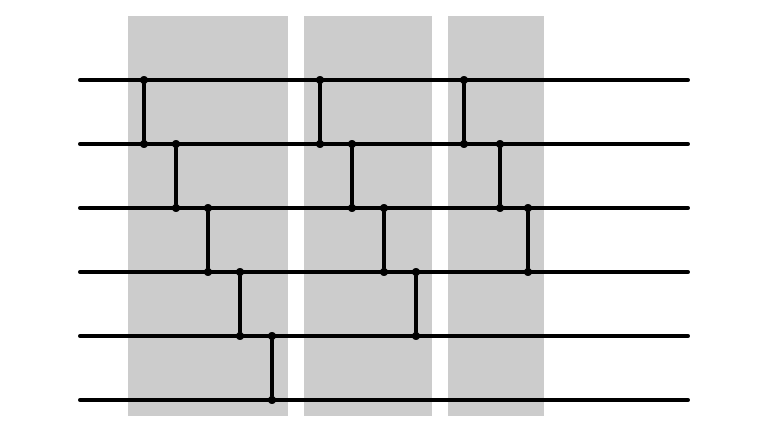
Bubble Sort: m = 3

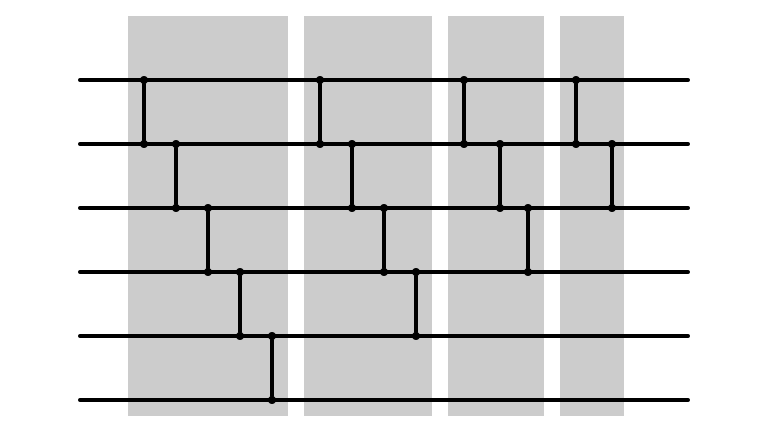
Bubble Sort: m = 2

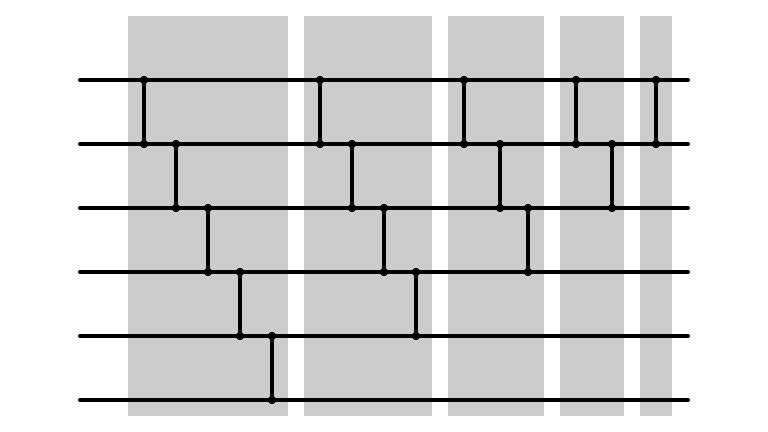
Bubble Sort Network

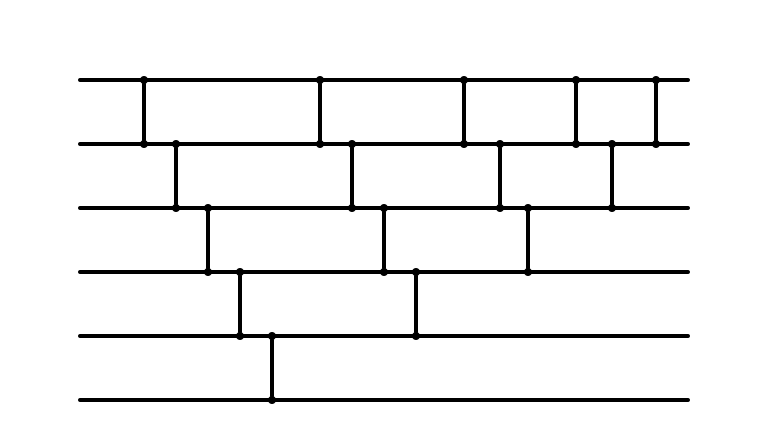
Bubble Sort Parallelized?

Does it Look Familiar?

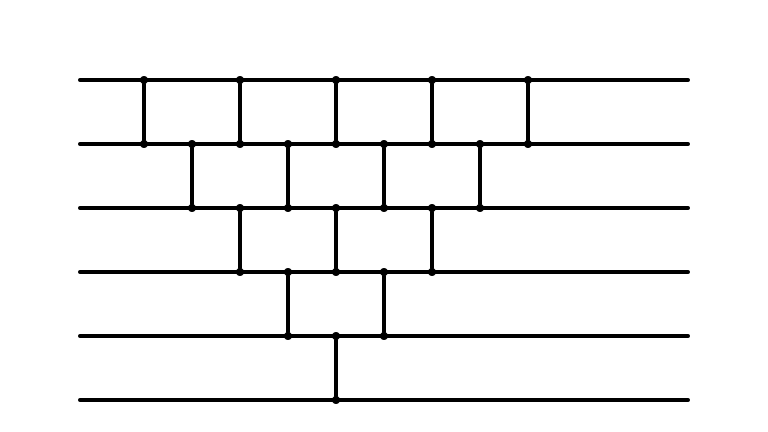
Huh

• Insertion sort and bubble sort perform precisely same operations
  • only differ in the order in which comparisons are made

• When fully parallelized, both are same sorting network

• Parallel versions are reasonably efficient
  • depth $2 (n - 1) - 1 = 2 n - 3$

Activity

Make a more efficient sorting network for 4 elements

Sorting Network for 4 Elements?

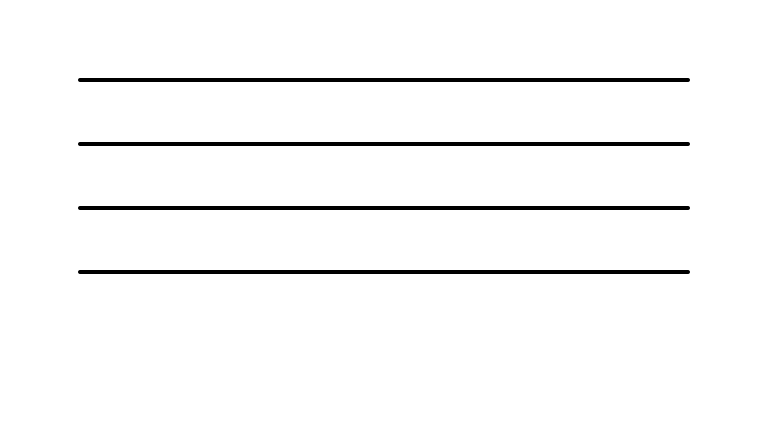
Sorting Vectors

How could we use this sorting network to sort Vectors with 4 lanes?

Implementation

How to implement the following parallel comparitor operations?

Example, In Pictures

• vec = [7, 4, 5, 6], vs = [1, 0, 3, 2]

Example, In Code

Original vector vec, shuffle vs, mask mask is true for all lanes corresponding to min comparator

var swapped = vec.rearrange(vs);
vec = vec.blend(vec.min(swapped, mask)
         .blend(vec.max(swapped, mask.not());

Optimal Network of Size 8

Testing It!

• sorting-networks.zip implements an optimal sorting network of size 8
• compares performance of sorting 1M blocks of size 8
  • vector sorting network vs insertion sort

Next Week

More shared data structures: linked lists!