Lecture 19: Mandelbrot and Sequential Consistency

COSC 273: Parallel and Distributed Computing

Spring 2023

Announcements

1. Lab 03 Due Friday MONDAY!!
   • Mandelbrot computations using Vector operations

   • Make sure your machine supports Vector ops today:

       > javac --add-modules jdk.incubator.vector SomeFile.java
       > java --add-modules jdk.incubator.vector SomeFile
     

     on HPC cluster, first run

     > module load amh-java/19.0.1 
     

Today

1. Mandelbrot and Vectors
2. A Sequentially Consistent Queue

Mandelbrot with Vectors

Mandelbrot, High Level

1. Define a grid of points
2. For each point
   • repeat until some condition is met:
     • perform arithmetic
   • record number of iterations

Baseline Code

float xStep = (xMax - xMin) / esc[0].length;
float yStep = (yMax - yMin) / esc.length;
for (int i = 0; i < esc.length; i++) {
    for (int j = 0; j < esc[0].length; j++) {
        int iter = 0;
        float cx = xMin + j * xStep;
        float cy = yMin + i * yStep;
        // do some arithmetic //
        esc[i][j] = iter;
    }
}

Baseline Code: Arithmetic

float zx = 0; float zy = 0;		
while (iter < maxIter && zx * zx + zy * zy < maxSquareModulus) {
    float z = zx * zx - zy * zy + cx;
    zy = 2 * zx * zy + cy;
    zx = z;
    iter++;
}
esc[i][j] = iter;

Observation

This code is the same for all points!

float zx = 0; float zy = 0;		
while (iter < maxIter && zx * zx + zy * zy < maxSquareModulus) {
    float z = zx * zx - zy * zy + cx;
    zy = 2 * zx * zy + cy;
    zx = z;
    iter++;
}

Differences:

1. input data (cx and cy)
2. stopping time (when while condition is not satisfied)

What Can Be Vectorized?

for (int i = 0; i < esc.length; i++) {
    for (int j = 0; j < esc[0].length; j++) {
        int iter = 0;
        float cx = xMin + j * xStep;
        float cy = yMin + i * yStep;
        float zx = 0; float zy = 0;
        while(/* some condition*/) { /* do stuff */}
        esc[i][j] = iter;
    }
}

New Inner Loop Structure

int step = /*something*/;
int max = /*something*/;
int j = 0;
for (; j < max; j += step) {

    /* initialize iter, cx, cy, zx, zy */
    
    /* do arithmetic */
}

How to Initialize Vectors?

• iter
  • previously 0
• cy
  • previously yMin + i * yStep
• cx
  • previously cx = xMin + j * xStep
• zx, zy

How to Perform Vector Arithmetic?

while (iter < maxIter && zx * zx + zy * zy < maxSquareModulus) {
    float z = zx * zx - zy * zy + cx;
    zy = 2 * zx * zy + cy;
    zx = z;
    iter++;
}
esc[i][j] = iter;

How To Check Termination?

while (iter < maxIter && zx * zx + zy * zy < maxSquareModulus) {
    float z = zx * zx - zy * zy + cx;
    zy = 2 * zx * zy + cy;
    zx = z;
    iter++;
}
esc[i][j] = iter;

General Advice

1. Start with “direct” translation of baseline code
   • READ THE Vector DOCUMENTATION
   • use masked operations/conditions on masks
2. Test variations
   • tradeoff: variables vs operations

Sequential Consistency

Concurrent Objects

1. An ADT (abstract data type) defines sequential correctness of an object
   • e.g., queue, stack, set, etc.
2. Concurrent objects allow for concurrent operations on the object

Rhetorical Question. What does it mean for a concurrent object to be “correct?”

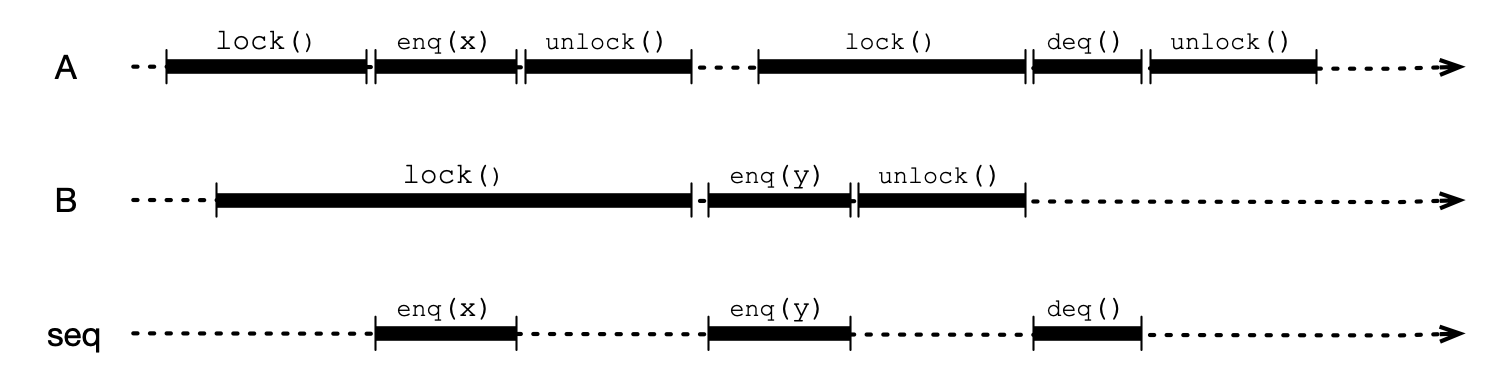
Sequential Consistency

An execution is sequentially consistent if all method calls can be ordered such that:

1. they are consistent with program order
2. they meet object’s sequential specification

An implementation of an object is sequentially consistent if

1. it guarantees every execution is sequentially consistent

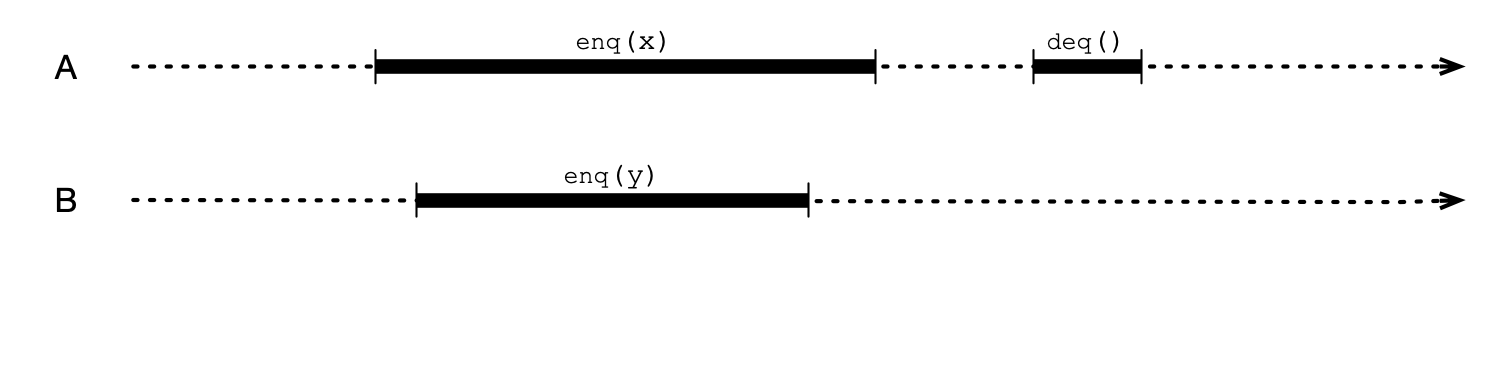
Example: A Sequentially Consistent Queue

An Array-Based Queue

public class LockedQueue<T> {
    int head, tail;
    T[] contents;
    Lock lock;
}

Enqueuing

    public void enq(T x) {
        lock.lock();
        try {
            items[tail] = x;
            tail++;
        } finally {
            lock.unlock();
        }
    }

Dequeueing

    public T deq() {
        lock.lock();
        try {
            T x = items[head];
            head++;
            return x;
        } finally {
            lock.unlock();
        }
    }

What Happens?

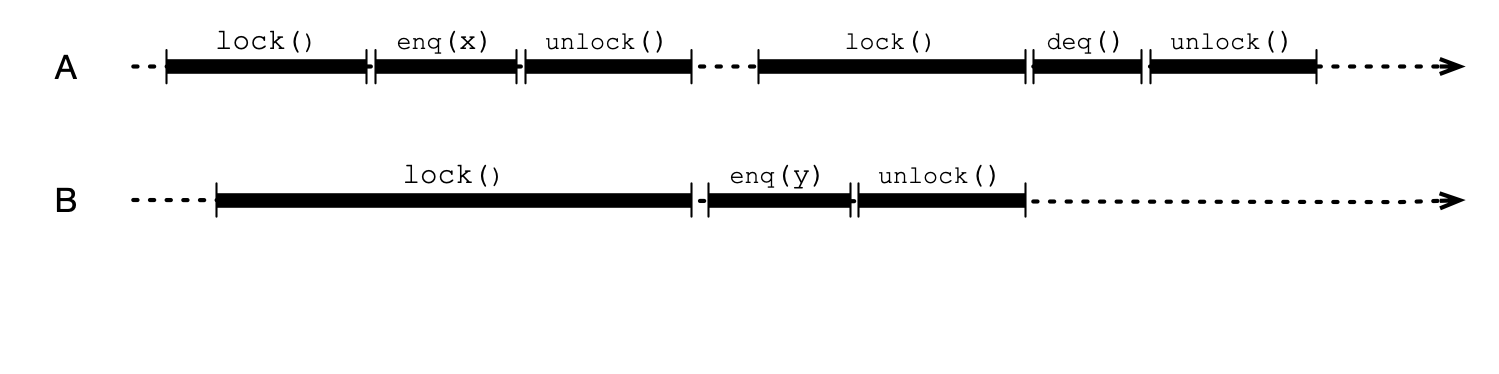
What Happens with Locks?

Equivalent Sequential Execution

Why is Queue Sequentially Consistent?

Questions

1. Can we achieve sequential consistency without resorting to locks?
   • again, this technique is essentially sequential
2. Is sequential consistency enough?

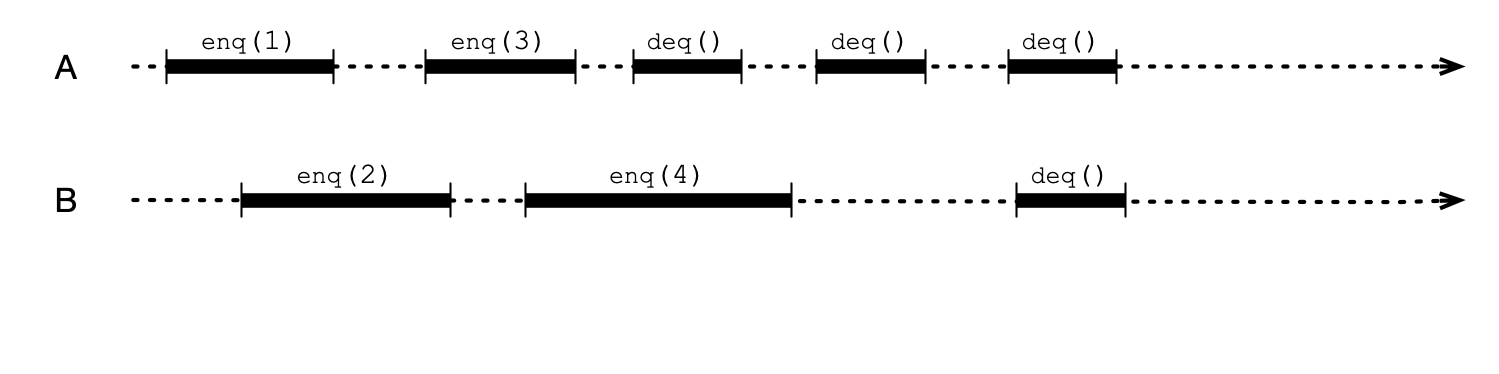
What are “Acceptable” Outcomes?

Next Time

Linearizability: A stronger notion of correctness for concurrent objects

• considers “wall clock” time in addition ot program order