Lecture 14: Computing the Mandelbrot Set

COSC 273: Parallel and Distributed Computing

Spring 2023

Outline

  1. Benchmarking Notes
  2. The Mandelbrot Set

Benchmarking Notes

To give “accurate” measure of efficiency:

  • test running time of method for many invocations
  • run several invocations before starting timing
    • “warm up” primes hardware with correct instructions

Benchmarking Demo

Lab 03: Mandelbrot Set

Draw this picture as quickly as possible!

Even Better: Animation

Source: Wikipedia

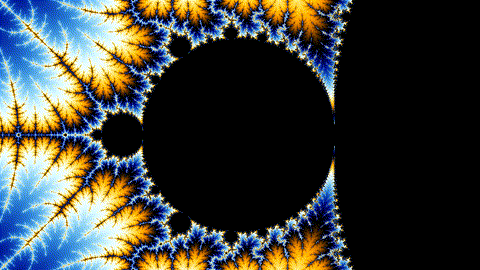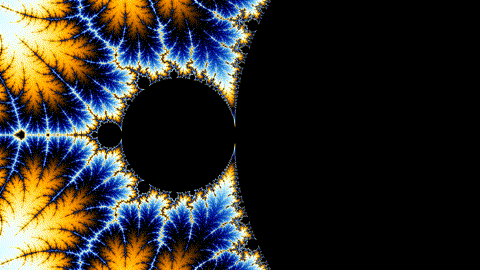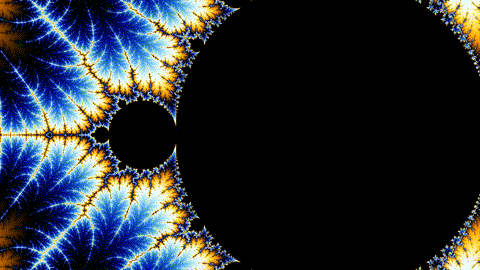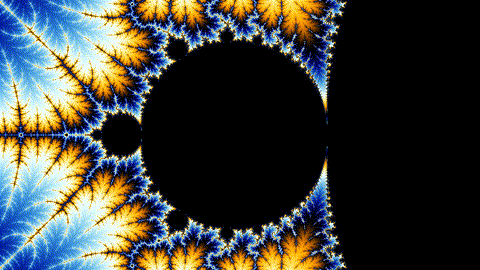
How?

The Mandelbrot set is a set of complex numbers that satisfy a certain property. We’ll need:

  1. (Re)view of complex numbers and arithmetic
  2. Iterated maps and Mandelbrot set definition
  3. Computing and visualizing the Mandelbrot set

Complex Numbers

Complex Numbers

Recall:

  • the imaginary number $i$ satisfies $i^2 = -1$
  • complex numbers are number of the form $a + b i$ where $a$ and $b$ are real
  • complex arithmetic:
    • $(a + b i) + (c + d i) = (a + c) + (b + d) i$
    • $(a + b i) \cdot (c + d i) = (a c - b d) + (a d + b c) i$
  • modulus (or length):
    • $|a + b i| = \sqrt{a^2 + b^2}$

Complex Plane

Associate complex number $a + b i$ with point $(a, b)$ in plane

Geometric View of Addition

Addition is vector addition:

Geometric View of Multiplication

Multiplication adds angles, multiplies lengths:

Iterated Operations

Fix a complex number $c$

  • Define sequence $z_1, z_2, z_3, \ldots$ by
    • $z_1 = c$
    • for $n > 1$, $z_{n} = z_{n-1}^2 + c$
  • What happens for different values of $c$?

Mandelbrot Set

The Mandelbrot set is the set $M$ of complex numbers $c$ such that the sequence $z_1, z_2, \ldots$ remains bounded (i.e., $|z_n|$ does not grow indefinitely)

Question

How can we determine if a given number $a + b i$ is in the Mandelbrot set?

Facts

  1. If $c$ satisfies $|c| > 2$, then $c$ is not in the Mandelbrot set.
  2. If $|c| \leq 2$ but some $z_n$ satisfies $|z_n| > 2$, then $c$ is not in the Mandelbrot set.

Observation. These facts give us a way of excluding points not in $M$. How?

Activity

Determine if the following points are in the Mandelbrot set:

  • $-1$
  • $i$
  • $i+1$
  • $-2$

Depicting the Mandelbrot Set

Make a grid of pixels!

Computing the Mandelbrot Set

Choose parameters:

  • $N$ number of iterations
  • $M$ maximum modulus ($M > 2$)

Given a complex number $c$:

  • compute $z_1 = c, z_2 = z_1^2 + c,\ldots$ until
    1. $|z_n| \geq M$
      • stop because sequence appears unbounded
    2. $N$th iteration
      • stop because sequence appears bounded
  • if $N$th iteration reached $c$ is likely in Mandelbrot set

Illustration

https://complex-analysis.com/content/mandelbrot_set.html

Drawing the Mandelbrot Set

  • Choose a region consisting of $a + b i$ with
    • $x_{min} \leq a \leq x_{max}$
    • $y_{min} \leq b \leq y_{max}$
  • Make a grid in the region
  • For each point in grid, determine if in Mandelbrot set
  • Color accordingly

Counting Iterations

Given a complex number $c$:

  • compute $z_1 = c, z_2 = z_1^2 + c,\ldots$ until
    1. $|z_n| \geq M$
      • stop because sequence appears unbounded
    2. $N$th iteration
      • stop because sequence appears bounded
  • if $N$th iteration reached $c$ is likely in Mandelbrot set

Color by Escape Time

  1. Color black in case 2 (point is in Mandelbrot set)
  2. Change color based on $n$ in case 1:
    • smaller $n$ are “farther” from Mandelbrot set
    • larger $n$ are “closer”

Lab 03

Input:

  • A square region of complex plane

Output:

  • Escape times for a grid of points in the region
  • A picture of corresponding region

Goal:

  • Compute escape times as quickly as possible