Lecture 08: Locality and Shortcuts

COSC 273: Parallel and Distributed Computing

Spring 2023

Up Now

• Lab 02: Computing Shortcuts
• HPC cluster instructions

Performance

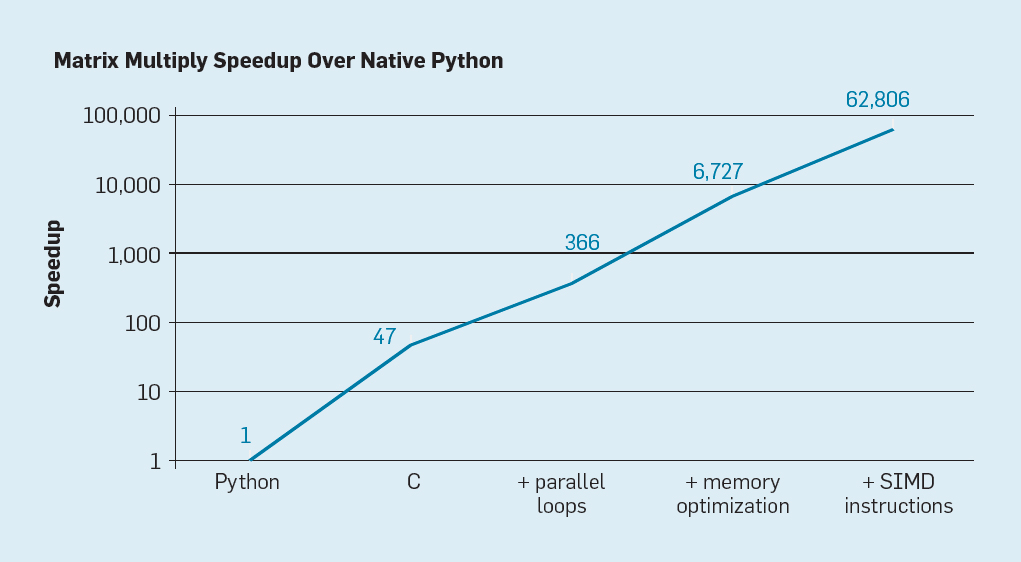
Last Time: Cost of Random Access

Linear Sum:

	float total = 0;
	for (int i = 0; i < size; ++i) {
	    int idx = linearIndex[i];
	    total += values[idx];
	}
	return total;

Random Sum:

	float total = 0;
	for (int i = 0; i < size; ++i) {
	    int idx = randomIndex[i];
	    total += values[idx];
	}
	return total;

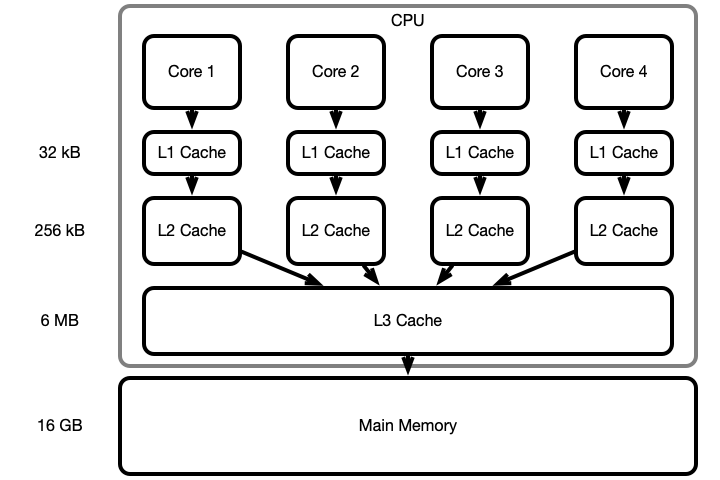
What Your Computer (Probably) Does

arr a large array

On read/write arr[i], search for arr[i] successively in

• L1 cache
• L2 cache
• L3 cache
• main memory

Copy arr[i] and surrounding values to L1 cache

• usually arr[i-a],...,arr[i+b] ends up in L1

This process is called paging

Cache Illustration

Performance Tuning

Be aware of your program’s memory access pattern

• reading values sequentially can be 10s of times faster than reading randomly or jumping around

Lab 02: Computing Shortucts

A Network

Matrix Representation of Distances

In Code

	float[][] shortcuts = new float[size][size];
	for (int i = 0; i < size; ++i) {
	    for (int j = 0; j < size; ++j) {
		float min = Float.MAX_VALUE;
		for (int k = 0; k < size; ++k) {
		    float x = matrix[i][k]; 
		    float y = matrix[k][j];
		    float z = x + y;
		    if (z < min)
			min = z;
		}
		shortcuts[i][j] = min;
	    }

Activity/Discussion

Questions.

1. Which accesses to matrix are sequential? Which are not?
2. How could we make all memory accesses sequential?
3. Which operations can be (easily) parallelized?

Question 1.

Which accesses to matrix are sequential? Which are not?

	float[][] shortcuts = new float[size][size];
	for (int i = 0; i < size; ++i) {
	    for (int j = 0; j < size; ++j) {
		float min = Float.MAX_VALUE;
		for (int k = 0; k < size; ++k) {
		    float x = matrix[i][k]; 
		    float y = matrix[k][j];
		    float z = x + y;
		    if (z < min)
			min = z;
		}
		shortcuts[i][j] = min;
	    }

Visualizaing Access Pattern

Question 2

How could we make all memory accesses sequential?

Code, Again

	float[][] shortcuts = new float[size][size];
	for (int i = 0; i < size; ++i) {
	    for (int j = 0; j < size; ++j) {
		float min = Float.MAX_VALUE;
		for (int k = 0; k < size; ++k) {
		    float x = matrix[i][k]; 
		    float y = matrix[k][j];
		    float z = x + y;
		    if (z < min)
			min = z;
		}
		shortcuts[i][j] = min;
	    }

Question 3

Which operations can be (easily) parallelized?

	float[][] shortcuts = new float[size][size];
	for (int i = 0; i < size; ++i) {
	    for (int j = 0; j < size; ++j) {
		float min = Float.MAX_VALUE;
		for (int k = 0; k < size; ++k) {
		    float x = matrix[i][k]; 
		    float y = matrix[k][j];
		    float z = x + y;
		    if (z < min)
			min = z;
		}
		shortcuts[i][j] = min;
	    }

Assignment Challenges

1. Optimize loops for linear memory access
2. Parallelize loops using multithreading

Suggestions

1. Get working solution on your computer first
2. Then test on the HPC cluster

[wrosenbaum@hpc-login1 lab02-shortcuts]$ cat shortcutTest.out 
|------|------------------|-------------|------------------|---------|
| size | avg runtime (ms) | improvement | iteration per us | passed? |
|------|------------------|-------------|------------------|---------|
|  128 |              184 |        0.05 |               11 |     yes |
|  256 |               56 |        0.82 |              294 |     yes |
|  512 |               19 |        9.22 |             6972 |     yes |
| 1024 |               85 |       33.15 |            12497 |     yes |
| 2048 |              257 |       88.33 |            33317 |     yes |
| 4096 |             1124 |      324.66 |            61095 |     yes |
|------|------------------|-------------|------------------|---------|