Lecture 07: Locality of Reference

COSC 273: Parallel and Distributed Computing

Spring 2023

Coming Soon!

• Lab 02: Computing Shortcuts
• HPC cluster instructions

Outline

1. Activity: Locality of Reference
   • download lec07-locality-of-reference.zip from website
2. Computer Architecture, Oversimplified
3. Computing Shortcuts

Two Stories

1. Multithreaded performance
   • embarrassingly parallel computaton
   • e.g., estimating $\pi$
2. Multithreaded correctness
   • e.g., Counter example
   • mutual exclusion (continued next week)

LocalAdder Class

Task. Create an array of random (float) values and compute their sum.

Two Implementations

Linear Sum:

	float total = 0;
	for (int i = 0; i < size; ++i) {
	    int idx = linearIndex[i];
	    total += values[idx];
	}
	return total;

Random Sum:

	float total = 0;
	for (int i = 0; i < size; ++i) {
	    int idx = randomIndex[i];
	    total += values[idx];
	}
	return total;

Tester

AdderTester:

• computes linear sum
• computes random sum
• compares running times

Parameters:

• STEP the step size been array tests
• START starting size value
• MAX maximum size value

Activity

Run AdderTester for a wide range of sizes:

• 1,000 – 10,000
• 10,000 – 100,000
• 100,000 – 1,000,000
• 1,0000,000 – 10,000,000
• 10,000,000 – 100,000,000

Questions.

1. How do running times compare between linear/random access for smaller arrays? What about larger arrays?

2. How does running time scale with linear/random access?

3. Did you expect to see the trend you see?

How do running times compare?

Can you explain the trend?

Architecture, Less Oversimplified

Idealized Picture

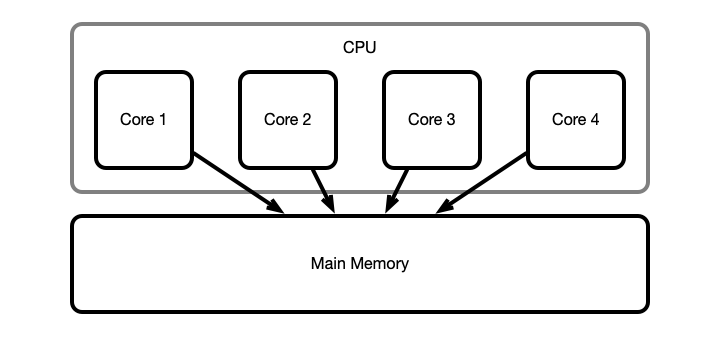
Unfortunately

Computer architechture is not so simple!

• Accessing main memory (RAM) directly is costly
  • ~100 CPU cycles to read/write a value!
• Use hierarchy of smaller, faster memory locations:
  • caching
  • different levels of cache: L1, L2, L3
  • cache memory integrated into CPU $\implies$ faster access

A More Accurate Picture

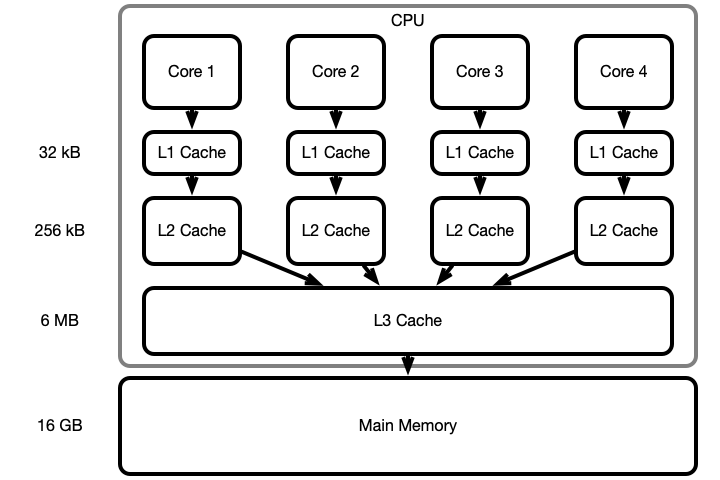
How Memory is Accessed

When reading or writing:

• Look for symbol (variable) successively deeper memory locations
  • L1, L2, L3, main memory
• Fetch symbol/value into L1 cache and do manipulations here
• When a cache becomes full, push its contents to a deeper level
• Periodically push changes down the heirarchy

Memory Access Illustrated

Why Is Caching Done? Efficiency!

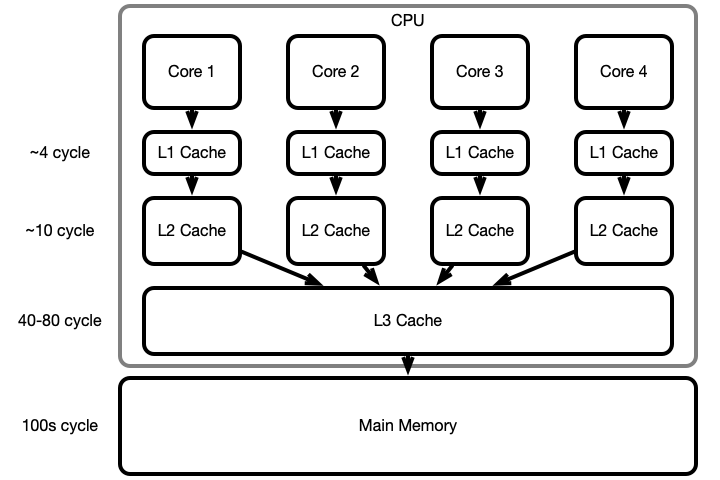
Why Caching Is Efficient

Heuristic:

• Most programs read/write to a relatively small number of memory locations often
• These values remain in low levels of the hierarchy
• Most commonly performed operation are performed efficiently

Why Caching is Problematic

Cache (in)consistency

• L1, L2 cache for each core
• Multiple cores modify same variable concurrently
• Only version stored in local cache modified quickly
• Same variable has multiple values simultaneously!

Takes time to propogate changes to values

• Shared changes only occur periodically!

What Your Computer (Probably) Does

arr a large array

On read/write arr[i], search for arr[i] successively in

• L1 cache
• L2 cache
• L3 cache
• main memory

Copy arr[i] and surrounding values to L1 cache

• usually arr[i-a],...,arr[i+a] ends up in L1

This process is called paging

Performance Tuning

Be aware of your program’s memory access pattern

• reading values sequentially can be 10s of times faster than reading randomly or jumping around

Lab 02: Computing Shortucts

A Network

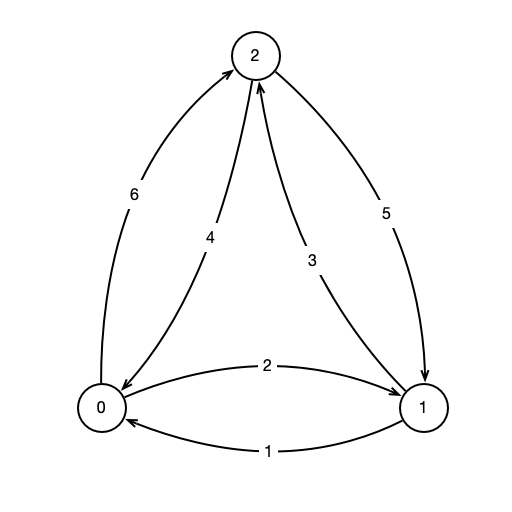
Network

• nodes and edges between nodes
  • nodes labeled $0, 1, \ldots, n$
  • directed edges $(i, j)$ from $i$ to $j$ for each $i \neq j$
• edges $(i, j)$ have associated weight, $w(i, j) \geq 0$
  • weight indicates cost or distance to move from $i$ to $j$

Shortcuts

What is cheapest path from 0 to 2?

A Problem

Given a network as above, for all $i \neq j$, find cheapest path of length (at most) 2 from $i$ to $j$

• weight of a path is sum of weight of edges
• convention: $w(i, i) = 0$
• a shortcut from $i$ to $j$ is a path $i \to k \to j$ where $w(i, k) + w(k, j) < w(i, j)$

Shortcut Distances

Representing Input

• \[D = \left( \begin{array}{ccc} 0 & 2 & 6\\ 1 & 0 & 3\\ 4 & 5 & 0 \end{array} \right)\]

Computing Output

• $D = (d_{ij})$
• Output $R = (r_{ij})$
  • $r_{ij}$ = shortcut distance from $i$ to $j$
  • computed by \(r_{ij} = \min_k d_{ik} + d_{kj}\)

Example

• \[D = \left( \begin{array}{ccc} 0 & 2 & 6\\ 1 & 0 & 3\\ 4 & 5 & 0 \end{array} \right)\]
• \[R = \left( \begin{array}{ccc} 0 & 2 & 5\\ 1 & 0 & 3\\ 4 & 5 & 0 \end{array} \right).\]

In Code

• Create a SquareMatrix object
• SquareMatrix stores a 2d array of floats called matrix
  • matrix[i][j] stores \(w(i, j)\)

Your Assignment

Write a program that computes shortcut matrix as quickly as possible!

• You’ll be given
  • getShortcutMatrixBaseline()
• Your assignment is to optimize the code to write
  • getShortcutMatrixOptimized ()

Assignment Challenges

1. Optimize memory access pattern for operations
   • make access pattern linear, when possible
2. Apply multithreading to get further speedup
   • partition the problem into smaller parts

Payoff: optimized program will be 10s of times faster on your computer, 100s of times faster on HPC cluster!