Lecture 16: Drawing General Graphs II

COSC 225: Algorithms and Visualization

Spring, 2023

Announcements

1. Assignment 07 posted, due Friday
2. Quiz Next Monday
   • Apply Tidy Tree algorithm by hand
3. Assignment 08 posted soon, due next Friday
4. Limited OH This Week (advising week)
   • No OH today
   • No OH on Thursday

Outline

1. AVSDF Circular Layouts
2. Force-directed Graph Layout

Goals

From Fruchterman and Reingold (1991):

1. Distribute the vertices evenly in the frame.
2. Minimize edge crossings.
3. Make edge lengths uniform.
4. Reflect inherent symmetry.
5. Conform to the frame.

Last Time: Circular Layouts

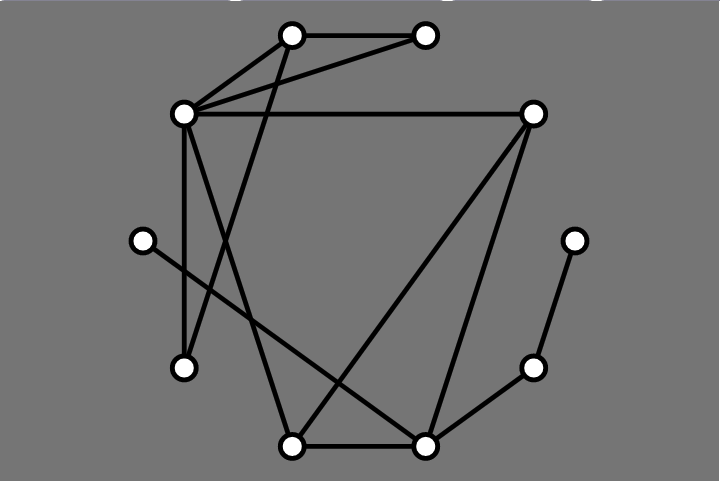
Simpler Challenge: pick an order for vertices

Mäkinen Procedure

1. Find two vertices of highest degree and add them to left/right sets
2. Repeat until all vertices are added to left or right:
   • compute (right neighbors) - (left neighbors) for each vertex
   • add vertex with largest value to right
   • add vertex with smallest value to left
3. Add left vertices on left side, right on right side

Mäkinen Results: Before

Mäkinen Results: After

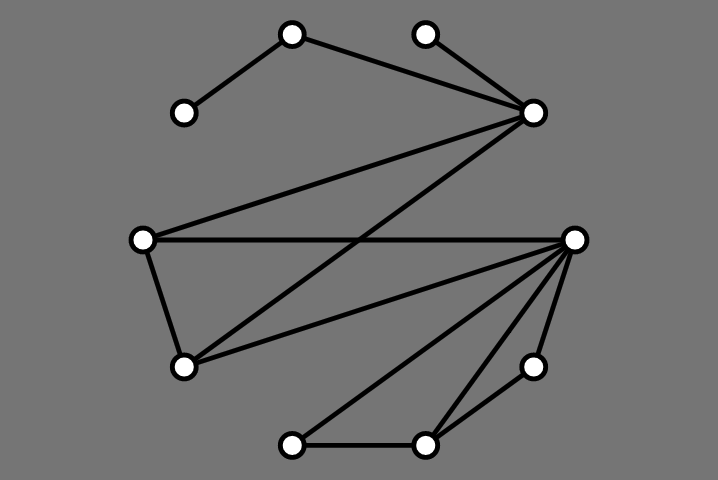
AVSDF Heuristic

Adjacent Vertex Smallest Degree First

• He & Sykora

Idea:

• perform depth-first search, starting from vertex of minimal degree
• always explore minimum degree neighbor first

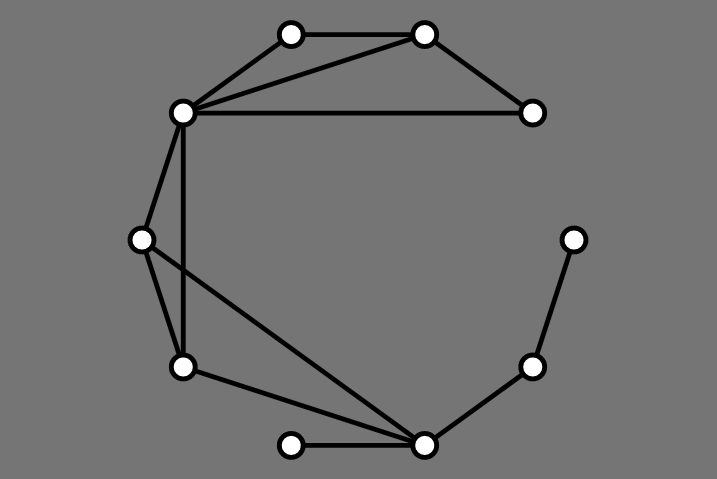
AVSDF Example

1: 2, 6, 3, 5
2: 1, 3, 5, 6
3: 1, 2, 6
4: 2, 5
5: 1, 2, 4
6: 1, 3

How To Implement AVSDF Efficiently

• What do we keep track of and store?
• How do we update data structures?
• How efficient is the procedure

AVSDF Initialization

	const order = [];
	const stack = [];
	const vertices = this.graph.vertices;
	const n = vertices.length;
	const placed = new Array(n).fill(false);
    
	vertices.sort((u, v) => {
	    return u.degree() - v.degree();
	});

	stack.push(vertices[0]);

Main Loop

while (stack.length > 0) {
  let vtx = stack.pop();		
  if (!placed[vtx.id]) {
    order.push(vtx);
    placed[vtx.id] = true;
    vtx.neighbors.sort((u, v) => {
      return v.degree() - u.degree();
    });
    for (let nbr of vtx.neighbors) {
      if (!placed[nbr.id]) { stack.push(nbr); }
    }}}

Running Time of Main Loop?

When Will Algorithm Fail?

1: Random Circular

2: Mäkinen Circular

3: AVSDF Circular

AVSDF Demo

Force-Directed Layout

A Different Approach

Don’t place vertices explicitly

Instead:

• associate graph with a physical system
• simulate the physical system
• let system evolve
• place vertices at final location according to evolution

Goals, Again

From Fruchterman and Reingold (1991):

1. Distribute the vertices evenly in the frame.
2. Minimize edge crossings.
3. Make edge lengths uniform.
4. Reflect inherent symmetry.
5. Conform to the frame.

Physical Simulation

1. All vertices should repel each other

2. Adjacent vertices should attract each other

Due to:

• Eades, 1984
• Fruchterman and Reingold, 1991
  • we’ll follow this paper

Competing Forces

All vertices:

function repulsiveForce (dist, k) {
  return k * k / dist;
}

function attractiveForce (dist, k) {
  return dist * dist / k;
}

Question

When do attractive and repulsive forces cancel out for adjacent vertices?

function repulsiveForce (dist, k) {
  return k * k / dist;
}

function attractiveForce (dist, k) {
  return dist * dist / k;
}

F&R Main Loop

For each vertex:

• compute net force on that vertex
  • find repulsive contribution from each other vertex
  • find attractive contribution from each neighbor
  • sum all contributions
• move each vertex according to net force
  • move in direction of net force
  • amount is min of net force and “temperature”
• update temperature

Repeat until “done”

Setting Parameters

Want k is “ideal” distance between vertices

• area = width * height
• n = vertices.length
• k = C * Math.sqrt(area / n)
  • k is “typical” distance if vertices are spread out
  • C some constant to be determined

Computing Forces I

• v at point (v.x, v.y)
• u at point (u.x, u.y)

What is distance from v to u?

Computing Forces II

Want (repsulive) force in direction of (deltaX, deltaY) with given amount (length): repulsiveForce(delta, k)

How to get this?

Adding All Repulsive Contributions

for (let v of vertices) {
  dx[v.id] = 0; dy[v.id] = 0;
  for (let u of vertices) {
    if (v != u) {
      let deltaX = v.x - u.x;
      let deltaY = v.y - u.y;
      let delta = Math.sqrt(deltaX * deltaX + deltaY * deltaY);
      dx[v.id] += (deltaX / delta) * repulsiveForce(delta, k);	
      dy[v.id] += (deltaY / delta) * repulsiveForce(delta, k);		
}}}

Similarly For Attractive Forces

for (let e of edges) {
  let v = e.vtx1; let u = e.vtx2;
  let deltaX = v.x - u.x; let deltaY = v.y - u.y;
  let delta = Math.sqrt(deltaX * deltaX + deltaY * deltaY);
  dx[v.id] -= (deltaX / delta) * attractiveForce(delta, k);
  dy[v.id] -= (deltaY / delta) * attractiveForce(delta, k);
  dx[u.id] += (deltaX / delta) * attractiveForce(delta, k);
  dy[u.id] += (deltaY / delta) * attractiveForce(delta, k);		
}

Applying Forces

for (let v of vertices) {
  let d = Math.sqrt(dx[v.id] * dx[v.id] + dy[v.id] * dy[v.id]);
  v.x += (dx[v.id] / d) * Math.min(d, temp);
  v.y += (dy[v.id] / d) * Math.min(d, temp);
  v.x = Math.max(v.x, xMin);
  v.x = Math.min(v.x, xMax);
  v.y = Math.max(v.y, yMin);
  v.y = Math.min(v.y, yMax);
}

Finally

Repeat:

• update positions
• decrease temperature

Stop when temperature is 0 (or some fixed number of iterations)

1: Random Circular

2: Mäkinen Circular

3: AVSDF Circular

4: Force Directed

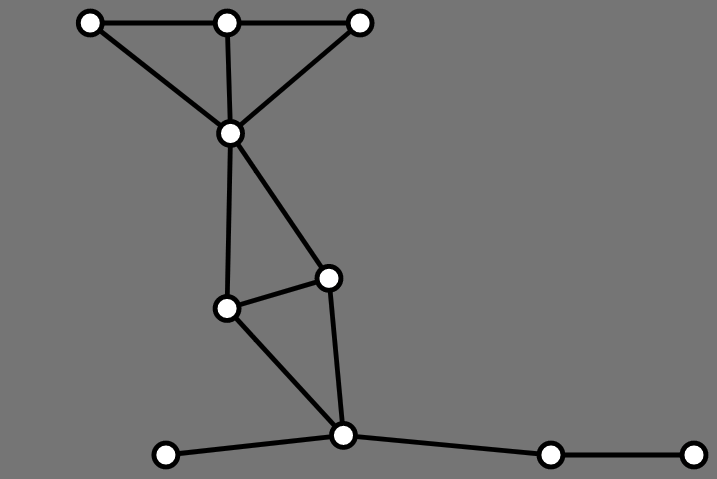
Okay

But it is WAY BETTER with animation

• Demo: lec16-graph-drawing.zip