Lecture 15: Drawing General Graphs I

COSC 225: Algorithms and Visualization

Spring, 2023

Announcements

  1. Assignment 07 posted, due Friday
  2. Assignment 08 posted soon, due next Friday
  3. Final Projects
    • work with partner
    • topic: open-ended
    • requirement: build an interactive site with a significant algorithmic component
  4. Limited OH This Week (advising week)
    • Short OH today
    • No OH on Thursday

Quiz 03, Question 1

Apply matrix(1, 1, -1, 1, 5, 2)

Outline

  1. Drawing General Graphs
  2. Circular Layouts
    • Mäkinen
    • AVSDF

Last Time: Drawing Trees I

Greedy Layout

Last Time: Drawing Trees II

Knuth Layout

Last Time: Drawing Trees III

Tidy Layout

Today

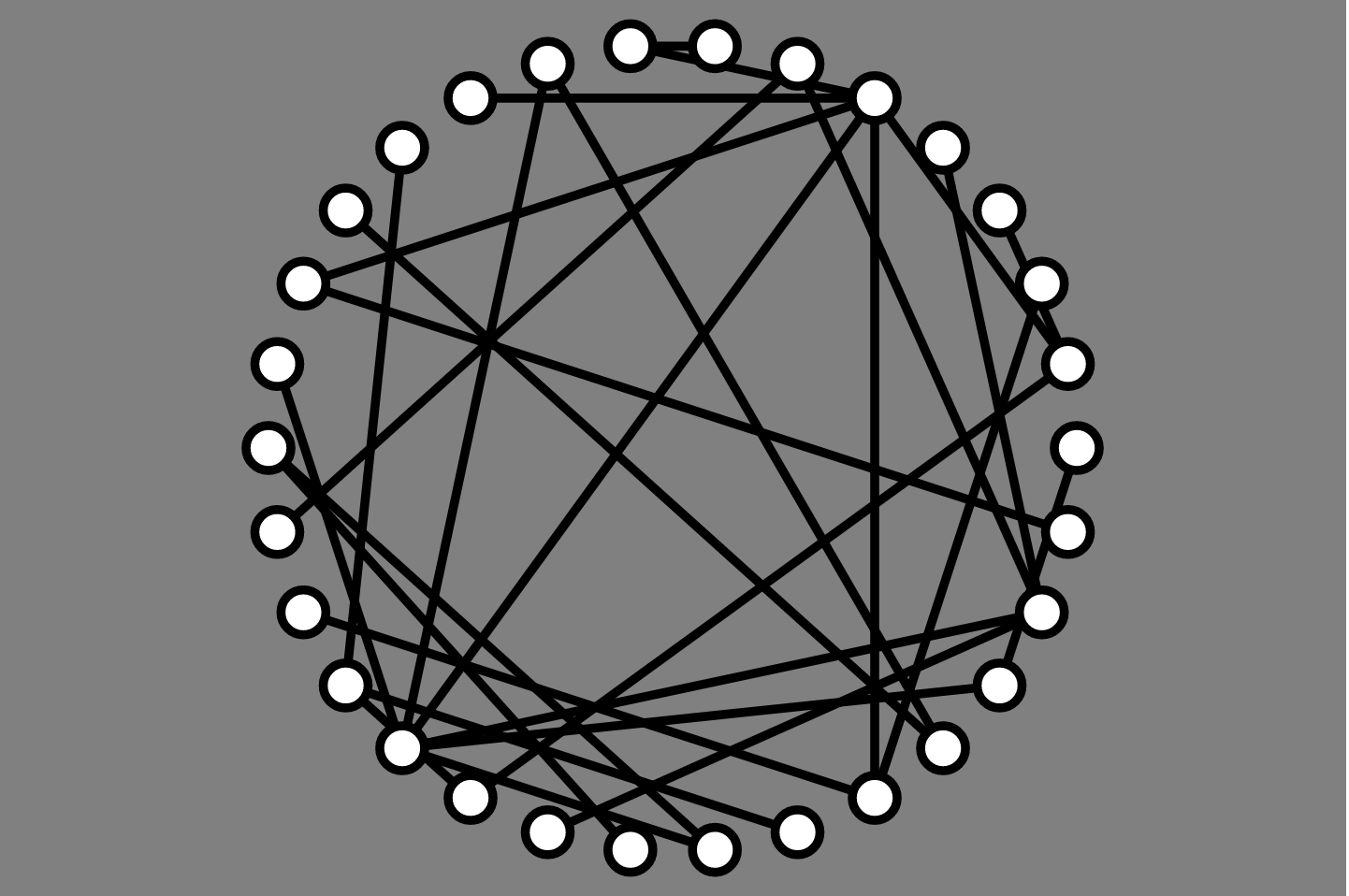
Drawing general graphs

Warmup Activity

Draw a graph with the following adjacency lists

1: 6, 4, 7
2: 8, 5, 3
3: 6, 2, 4
4: 5, 3, 1
5: 4, 2, 7
6: 1, 3, 8
7: 5, 8, 1
8: 2, 6, 7

Random Layout

What Does Graph Look Like?

More Generally

What might we want in a graph layout?

Desiderata

From Fruchterman and Reingold (1991):

  1. Distribute the vertices evenly in the frame.
  2. Minimize edge crossings.
  3. Make edge lengths uniform.
  4. Reflect inherent symmetry.
  5. Conform to the frame.

Interesting Question

Which graphs can be drawn without any edge crossings?

  • such graphs are called planar graphs

Minimal Non-planar Graphs

Characterization of Planar Graphs

Algorithmic Results

There are efficient algorithms for

  1. detecting if a graph is planar
  2. drawing a planar graph without edge crossings, e.g.:
    • Auslander-Parter 1961
    • Lempel-Even-Cederbaum 1967
    • …

Implementing one would make an awesome final project!

Minimizing Edge Crossings

What about non-planar graphs? (Most graphs are not planar!)

Question. Can we efficiently draw graphs so as to minimize the number of edge crossings?

Answer. No!

  • there is no known efficient algorithm for this task

More precisely. The following problem is NP-complete

  • Input: A graph $G$ and a natural number $k$
  • Output: “yes” if $G$ can be drawn with at most $k$ crossings, and “no” otherwise

General Graph Drawing

Focus on heuristics

  • do not guarantee that output minimized edge crossings, etc
  • nonetheless have reasonably good results for the graphs we care about
  • typically “simple” procedures

Two (of many) Approaches

  1. Circular Layouts (today)
    • fix vertices lie on a circle
    • pick an ordering of vertices to illustrate some graph features
  2. Physical simulation layouts (Wednesday)
    • force-directed graphs
      • adjacent vertices attract each other (somewhat)
      • non-adjacent vertices repel each other
    • simulate physical system to determine vertex placement

Circular Layouts

Progression I: Random

Progression II: Circular

Progression III: AVSDF

Starting Point

Framework from graph/DFS demos

  • Graph object stores lists of vertices/edges
  • Vertex object stores adjacency list (neighbors), has x, y
  • Edge object represents a pair of vertices
  • GraphVisualizer moderates interactions between site and Graph instance
    • draws vertices/edges
    • responds to user interactions

Adding Interactions

Previously:

  • click to add vertices
  • click pair of vertices to add edge

Added:

  • hover to highlight a vertex and its neighbors
  • demo: lec15-graph-drawing.zip

Implementing Hover Interactions

Added event listener to each vertex element

	elt.addEventListener("mouseover", (e) => {
	    this.muteAll();
	    this.unmuteVertex(vtx);
	    this.highlightVertex(vtx);
	    for (let nbr of vtx.neighbors) {
		this.highlightVertex(nbr);
		this.highlightEdge(this.graph.getEdge(vtx, nbr));
	    }
	});

	elt.addEventListener("mouseout", (e) => {
	    this.unmuteAll();
	    this.unhighlightAll();
	});

Circular Embeddings

Setup: Graph with $n$ vertices. How to set locations on a circle?

Circular Embedding in Code

this.setLayoutCircle = function (cx, cy, r) {
let vertices = this.graph.vertices;
let n = vertices.length;
for (let i = 0; i < n; i++) {
  vertices[i].x = r * Math.cos(2 * Math.PI * i / n) + cx;
  vertices[i].y = r * Math.sin(2 * Math.PI * i / n) + cy;
}}

Simplified Problem

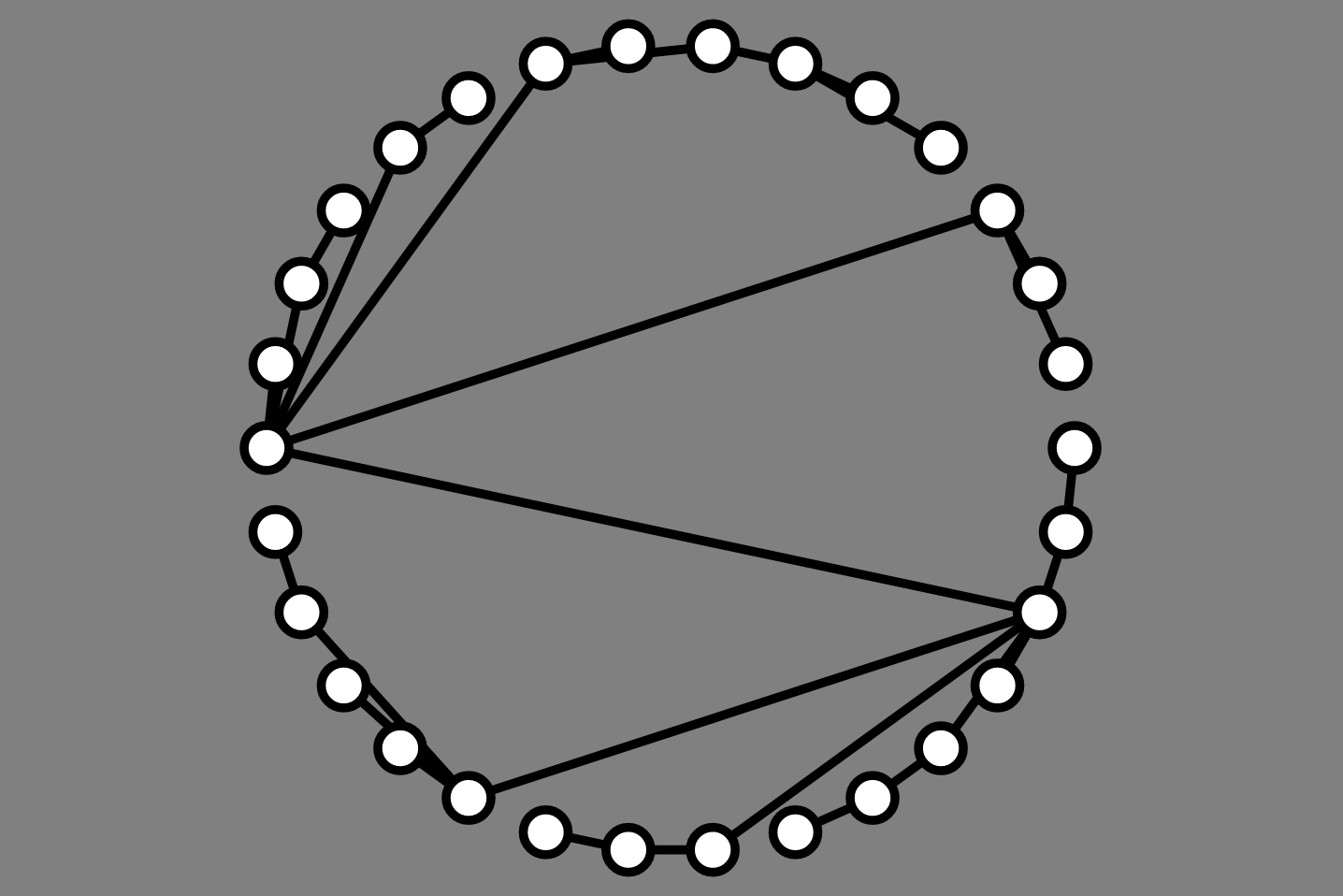
Now that we can draw vertices evenly around a circle, we can focus on the order in which to add vertices

  • which ordering minimizes edge crossings?
    • no easier than general problem!
  • which ordering is most informative?
  • which ordering looks nice?

Mäkinen Heuristic

Basic idea:

  • split vertices into left and right sets
  • vertices with more left neighbors placed on left side
    • sim for right side

Mäkinen Procedure

  1. Find two vertices of highest degree and add them to left/right sets
  2. Repeat until all vertices are added to left or right:
    • compute (right neighbors) - (left neighbors) for each vertex
    • add vertex with largest value to right
    • add vertex with smallest value to left
  3. Add left vertices on left side, right on right side

Mäkinen Example

1: 2, 6, 3, 5
2: 1, 3, 5, 6
3: 1, 2, 6
4: 2, 5
5: 1, 2, 4
6: 1, 3

How To Implement Mäkinen Efficiently

  • What do we keep track of and store?
  • How do we update data structures?
  • How efficient is the procedure

Mäkinen Procedure, Again

  1. Find two vertices of highest degree and add them to left/right sets
  2. Repeat until all vertices are added to left or right:
    • compute (right neighbors) - (left neighbors) for each vertex
    • add vertex with largest value to right
    • add vertex with smallest value to left
  3. Add left vertices on left side, right on right side

Data Structures

	const vertices = this.graph.vertices;
	const n = vertices.length;
	const leftPlaced = [];
	const rightPlaced = [];
	const placed = new Array(n).fill(false);
	const leftCount = new Array(n).fill(0);
	const rightCount = new Array(n).fill(0);
	let placedCount = 2;

Initialization

	vertices.sort((u, v) => {
	    return u.degree() - v.degree();
	});

	// two highest degree vertices go on left and right sides
	let left = vertices[n-1];
	leftPlaced.push(left);
	placed[left.id] = true;
	let right = vertices[n-2];
	rightPlaced.push(right);
	placed[right.id] = true;

Main Loop I

for (let vtx of left.neighbors) { leftCount[vtx.id]++; }
for (let vtx of right.neighbors) { rightCount[vtx.id]++; }

for (let vtx of vertices) {
  if (!placed[vtx.id]) {
    left = vtx;
    right = vtx;
    break;
  }}

Main Loop II

// set right and left to be the vertices maximizing and
// minimizing (respectively) the quantity rightCount -
// leftCount
for (let vtx of vertices) {
  if (/* most right - left nbrs */) {
    right = vtx;
  }

  if (/* least right - left nbrs  */) {
    left = vtx;
  }}

What is Overall Running Time?

Assume graph has $n$ vertices, $m$

See Demo

AVSDF Heuristic

Adjacent Vertex Smallest Degree First

  • He & Sykora

Idea:

  • perform depth-first search, starting from vertex of minimal degree
  • always explore minimum degree neighbor first

AVSDF Example

1: 2, 6, 3, 5
2: 1, 3, 5, 6
3: 1, 2, 6
4: 2, 5
5: 1, 2, 4
6: 1, 3

How To Implement AVSDF Efficiently

  • What do we keep track of and store?
  • How do we update data structures?
  • How efficient is the procedure

AVSDF Initialization

	const order = [];
	const stack = [];
	const vertices = this.graph.vertices;
	const n = vertices.length;
	const placed = new Array(n).fill(false);
    
	vertices.sort((u, v) => {
	    return u.degree() - v.degree();
	});

	stack.push(vertices[0]);

Main Loop

while (stack.length > 0) {
  let vtx = stack.pop();		
  if (!placed[vtx.id]) {
    order.push(vtx);
    placed[vtx.id] = true;
    vtx.neighbors.sort((u, v) => {
      return v.degree() - u.degree();
    });
    for (let nbr of vtx.neighbors) {
      if (!placed[nbr.id]) { stack.push(nbr); }
    }}}

Running Time of Main Loop?

When Will Algorithm Fail?

AVSDF Demo

Next Time

Force-directed layout