Lecture 13: Drawing Binary Trees I
COSC 225: Algorithms and Visualization
Spring, 2023
Annoucements
- Assignment 06 due tonight
- Assignment 07 posted soon
- make a site that incorporates recursion and coordinate transformation to make a self-similar image
- due next Monday
- Quiz this Wednesday: coordinate transformations
- define a
matrixtransformation given transformation’s geometric description - given a
matrixand original image, draw the transformed image
- define a
Outline
- Binary Trees
- Activity: Drawing Binary Trees by Hand
- Aesthetic and Pragmatic Principles
- Greedy Procedure
- Knuth Layout
A While Back
We illustrated the depth-first search algorithm on graphs
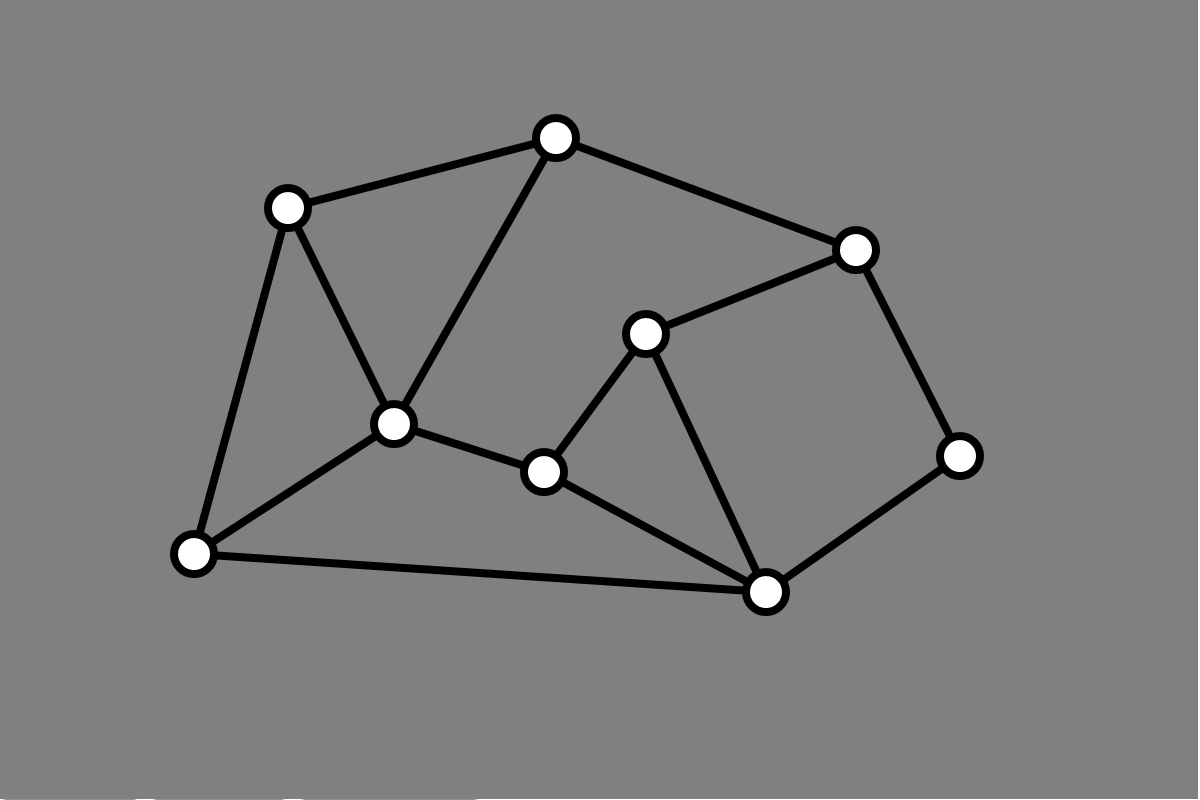
A While Back
We illustrated the depth-first search algorithm on graphs
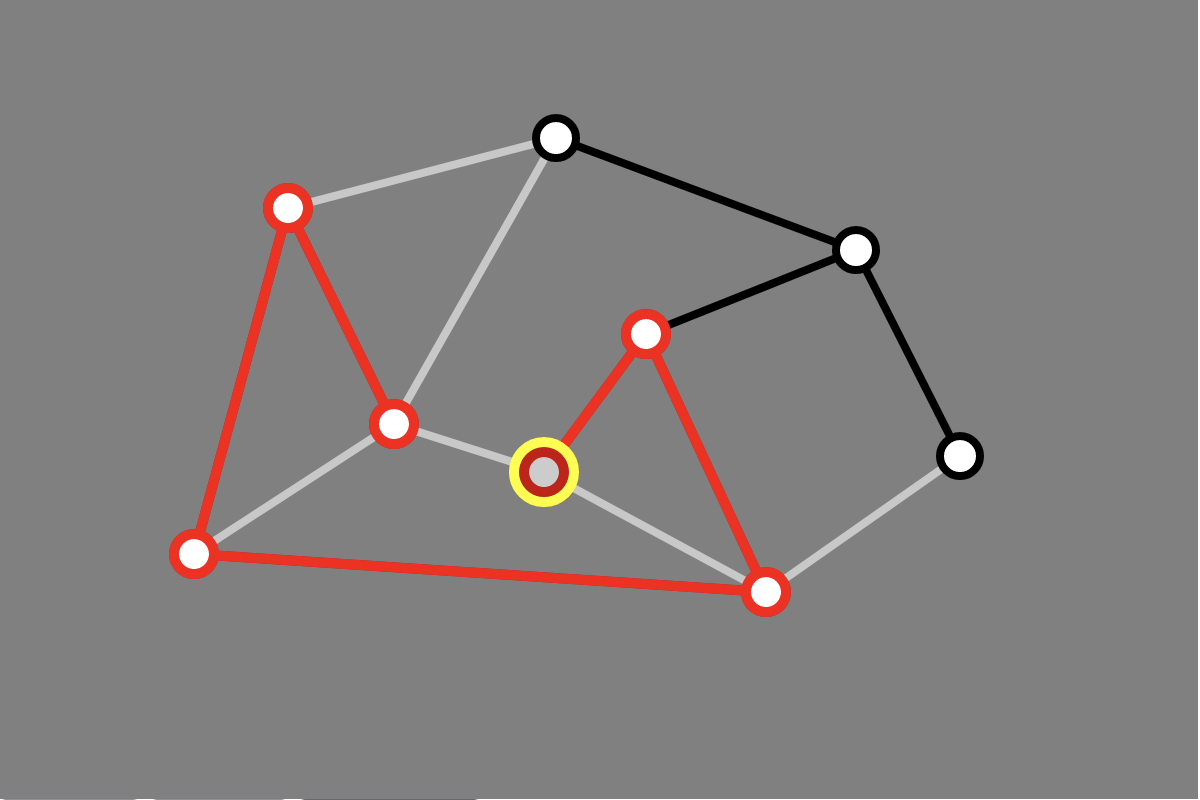
Interaction
User drew input graph graph by hand
- from clicks, obtained graph structure
- geometry of graph layout defined with graph
Graph Drawing
Input. A graph
- vertices
- edges
Output. A drawing of the graph
- visual representation of vertices
- geometric locations
- usually “points”
- visual representation of edges
- usual lines or curves between vertices
This Week
Algorithms for drawing binary trees
Recall
A (rooted) binary tree consists of
- a set $V$ of vertices
- a root vertex
- each vertex has:
- a left child (possibly null)
- a right child (possibly null)
satisfying:
- the root is not anyone’s child
- every node is the child of exaclty one node
- every node is a descendant of the root
Example
V = {0, 1, 2, 3, 4}root = 0left(0) = 2, right(0) = 3left(3) = 4, right(3) = 1- unassigned children are
null
Activity: Draw a Tree
V = {0,...,13}
root: 0
left(0) = 1, right(0) = 2
left(1) = 3, right(1) = 4
right(2) = 5
left(4) = 6, right(4) = 7
right(5) = 8
left(8) = 9
left(9) = 10, right(9) = 11
left(10) = 12, right(10) = 13
You Drew This, Right?
How About This?
What Did You Draw?
Questions
- What information do we want to convey about the tree?
- What constraints might we have on our drawing?
- What aesthetic considerations might we have?
- when does a tree “look nice?”
What Information Should the Drawing Convey?
What Constraints Should we Consider?
Aesthetic Considerations?
First Principle
Aesthetic Principle 1. Vertices at the same depth should lie along a horizontal line with deeper nodes lower than shallower nodes.
- what physical requirements does this impose?
Physical Limitation
Have to contend with width
- What can we do about it?
Optimal Layout?
How can we achieve minimum possible width subject to
- lower bound on horizontal spacing
- Aesthetic Principle 1
Greedy Layout
Idea
- draw vertices in rows according to depth
- depth = distance from root
- root goes alone in the top row, next row at depth 1, etc.
- draw each row with vertices from “left to right”
- what does this mean?
Promise
- Use as few columns as possible!
- minimize width requirement
Greedy Layout Illustrated
V = {0,...,7}
root: 0
left(0) = 1, right(0) = 2
left(1) = 3, right(1) = 4
right(2) = 5
left(4) = 6, right(4) = 7
How to Implement Greedy Layout?
Input: tree (just the root?)
Output: row and column for each node
How to Get Depths of Nodes?
My implementation:
- set depth when each vertex is added
- depth of a vertex is parent’s depth + 1
- store a
Map:- keys are vertex IDs
- values are depths
How to Get Columns?
Observation. If $u$ is a left child of $v$ and $w$ is a right child of $v$, then $u$ should be in a column to the left of $v$.
Idea. Starting from the root:
- place vertex in the left-most un-assigned column in its row (depth)
- place left descendants
- place right descendants
This is pre-order traversal!
Column Assignment Illustrated
V = {0,...,7}
root: 0
left(0) = 1, right(0) = 2
left(1) = 3, right(1) = 4
right(2) = 5
left(4) = 6, right(4) = 7
Greedy Layout in JavaScript
Computing Depths:
const BinaryTree = function (root) {
this.depths = new Map();
...
this.addLeftChild = function (parentID, childID) {
...
this.depths.set(childID, this.depths.get(parentID) + 1);
}
}
Greedy Layout in JavaScript
Getting vertices in “pre-order”
this.verticesPreOrder = function (from = this.root) {
let vertices = [];
vertices.push(from);
if (from.left != null)
vertices = vertices.concat(this.verticesPreOrder(from.left));
if (from.right != null)
vertices = vertices.concat(this.verticesPreOrder(from.right));
return vertices;
Greedy Layout in JavaScript
Getting Rows and Columns
this.setLayoutGreedy = function () {
const vertices = this.tree.verticesPreOrder();
const depths = this.tree.depths;
...
const cols = []; // current col for each row, initialized to 0
...
for (let vtx of vertices) {
let row = depths.get(vtx.id)
let col = cols[row];
cols[row]++;
/* set position of vtx to this row and col */
}}
Demo
lec13-binary-tree.zip
What is Missing?

Second Principle
Aesthetic Principle 2. The left child of any node should appear to the left of its parent, and a right child should appear to the right of its parent.
How to Achieve Principles 1 and 2?
Knuth’s Layout Algorithm
Rows and Columns
- rows are defined by depth (Aesthetic Principle 1)
- columns are “in-order” traversal order
- each vertex gets own column
- guarantees
- left descendants to the left
- right descenadants to the right
In-order Traversal
In-order Traversal in Code
this.verticesInOrder = function (from = this.root) {
let vertices = [];
if (from.left != null)
vertices = vertices.concat(this.verticesPreOrder(from.left));
vertices.push(from);
if (from.right != null)
vertices = vertices.concat(this.verticesPreOrder(from.right));
return vertices;
Knuth’s Layout in Code
this.setLayoutKnuth = function () {
const vertices = this.tree.verticesInOrder();
const depths = this.tree.depths;
for (let i = 0; i < vertices.length; i++) {
let vtx = vertices[i];
let depth = depths.get(vtx.id);
/* set vtx location to row depth, column i */
}
}
Result
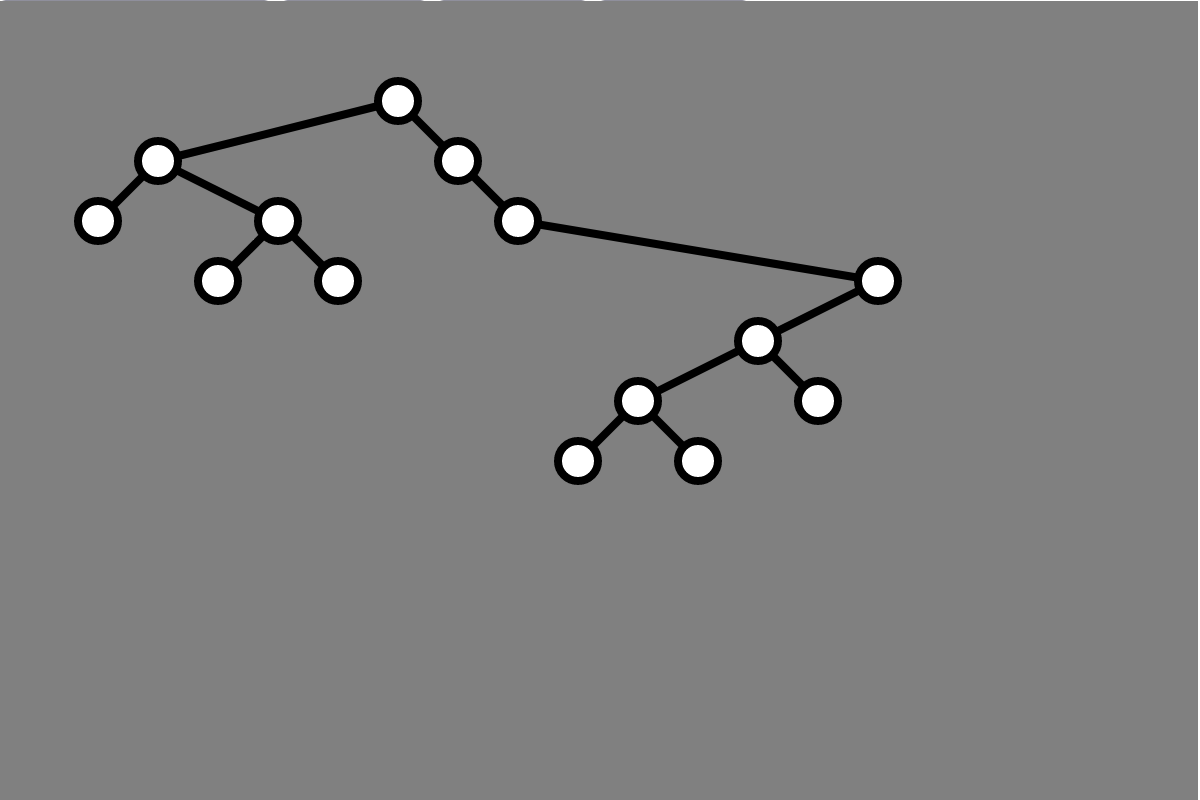
Demo, Again
lec13-binary-tree.zip
What’s Not to Like?
Result Again

Third Principle
Aesthetic Principle 3. If a node has two children, it’s $x$-coordinate should be the midpoint of its childrens’ $x$-coordinates
Questions (Next Time)
- How can we satisfy all three aesthetic principles?
- How can all be satisfied while also minimizing the width of the drawing?
- What tradeoffs are we forced to make balancinng these principles?