Lecture 12: Coordinate Transformations, Recursion & Self-similarity II
COSC 225: Algorithms and Visualization
Spring, 2023
Annoucements
Assignment 06 Due Friday MONDAY!!!
- tester later this week
Outline
- Koch Curve
- SVG Groups, Transformations, and Composition
- Matrix Transformation Activity
- Tree Example
Motivation: Self-Similarity

Example: Koch Curve I
How did we make the snowflake fractal?
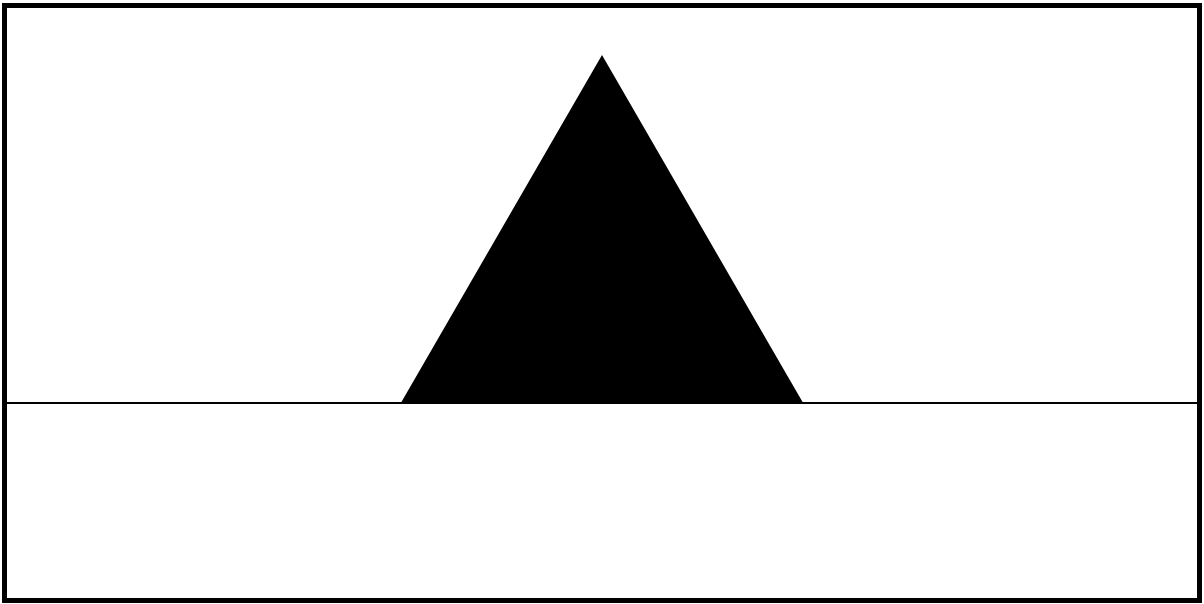
Step 1: define a basic shape
Example: Koch Curve II
How did we make the snowflake fractal?

Step 2: define sub-shapes for basic shape
Example: Koch Curve III
How did we make the snowflake fractal?

Step 3: recurse
Example: Koch Curve IV
How did we make the snowflake fractal?

Step 3: recurse
Observation

Each iteration draws a bunch of transformed copies of the original shape
Activity
Draw two iterations of the Koch curve!
lec11-koch-step.zip
The Basic Shape

In koch.js:
-
drawSegment(x1, y1, x2, y2)will draw the the basic shape transformed start at(x1, y1)and end at(x2, y2) - in original,
(x1, y1, x2, y2) = (0, 100, 600, 100),
How to Add First Iteration?

The Second Iteration?

This Would Be Annoying!

Composition
From last time: transformations compose
- perform transformation 1, then transformation 2
- transformation 2 is performed relative to transformation 1
Transformed
Transformed Coordinates
Element in New Coordinates
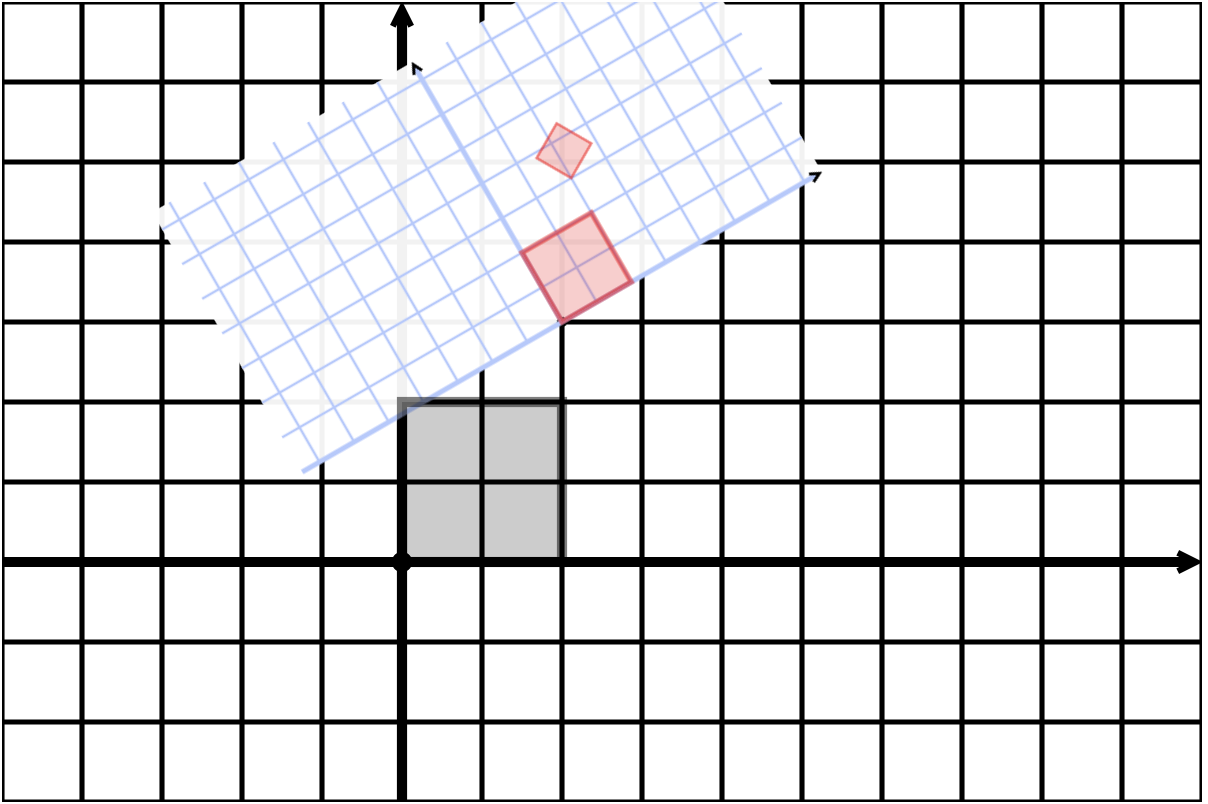
New New Coordinates
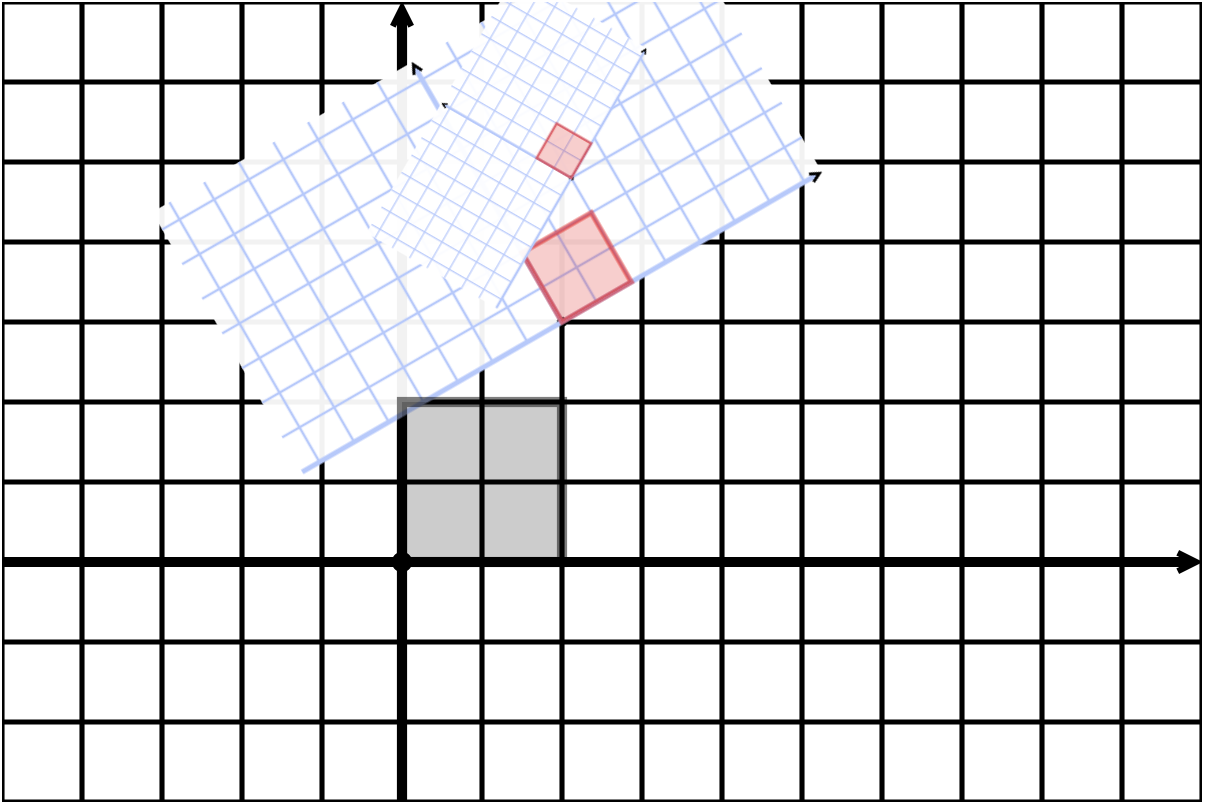
Koch Revisited
To draw a Koch segment:
- Change to local coordinates for that segment
- Draw a Koch segment
- relative to local coordinates instructions are the same as original segment
- Recursively draw a Koch segment on each sub-segment
Koch with Coordinates

The <g> Element
In SVG, <g> is a group element
- all elements in the same
<g>are drawn together - transformations of
<g>are applied to all elements in the<g> -
<g>elements can be nested- transformations of nested elements are composed
Example
<rect width="20" height="20" fill="black">
<g transform="translate(30, 20) rotate(45)">
<rect width="20" height="20" fill="black">
<g transform="translate(30, 20)">
<rect width="20" height="20" fill="black">
</g>
</g>
Drawing Koch Recursively
DrawKoch(parentGroup, transformation):
create and transform curGroup for this segment
draw this segment to curGroup
DrawKoch(curGroup, transformation for first sub-segment)
DrawKoch(curGroup, transformation for second sub-segment)
DrawKoch(curGroup, transformation for third sub-segment)
DrawKoch(curGroup, transformation for fourth sub-segment)
Koch Demo
lec12-koch-step.zip
The matrix Reloaded
In SVG you can perform an affine transformation
- vector $(1, 0)$ to $(a, b)$
- vector $(0, 1)$ to $(c, d)$
- point $(0, 0)$ to $(e, f)$
with
transform=matrix(a, b, c, d, e, f)
For Your Consideration
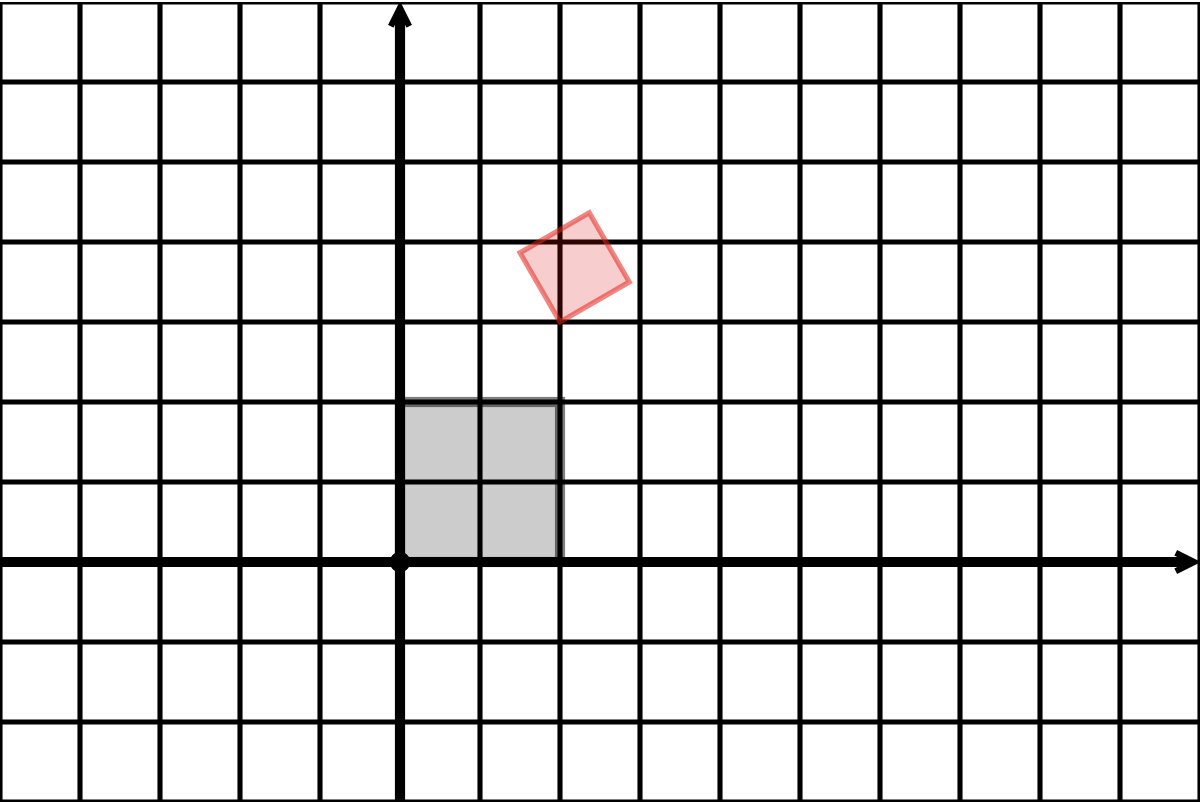
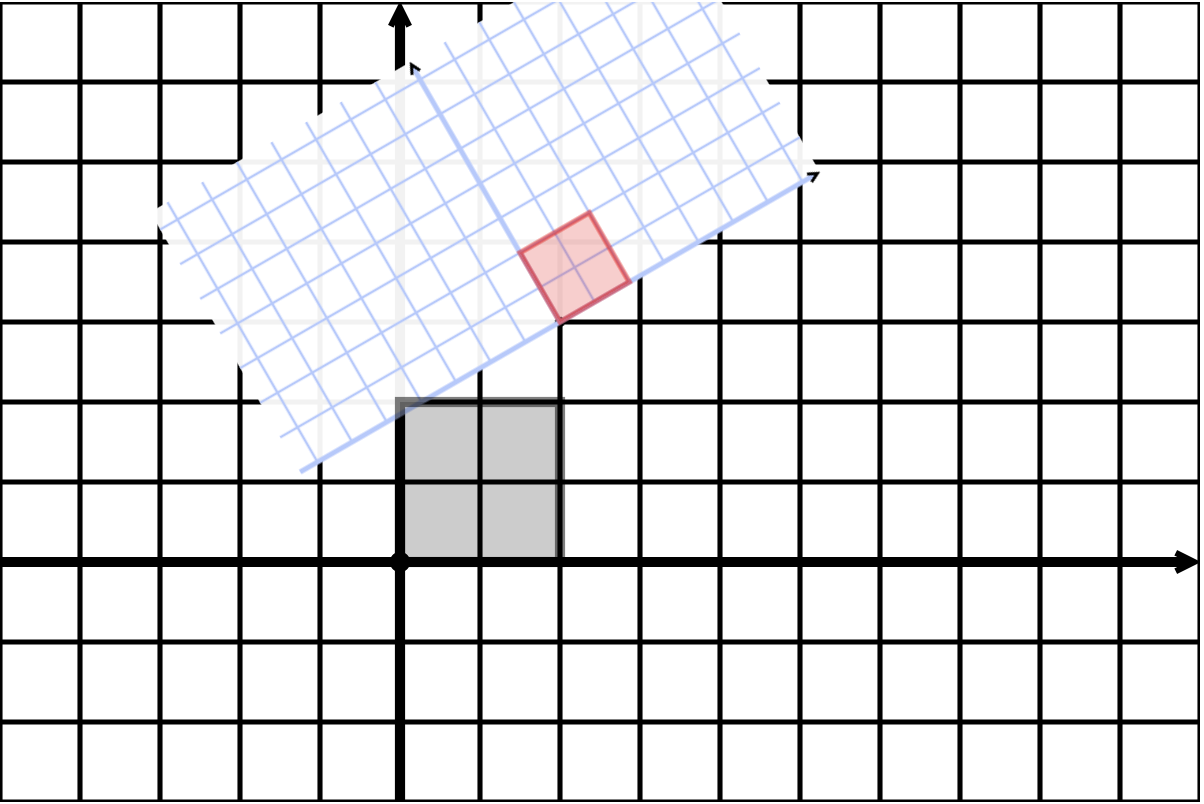
Two squares

Activity: Find the matrix

Question. What matrix transformation will transform the outer square to the inner square?
How Did I Make This?
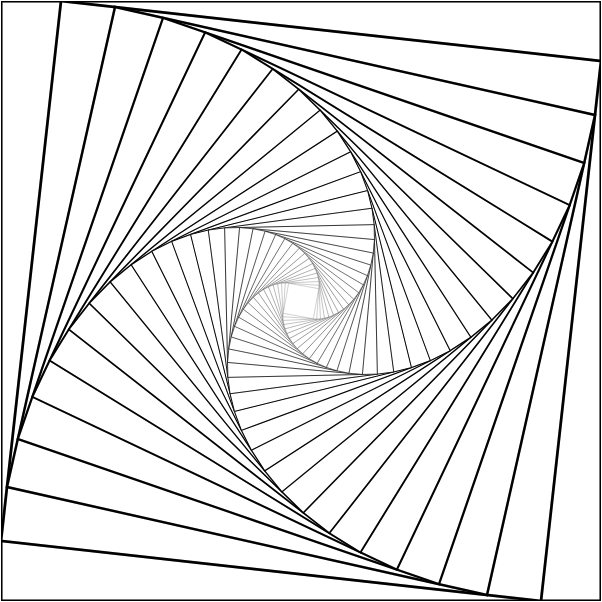
Recursive Squares Demo
lec12-recusrive-squares.zip
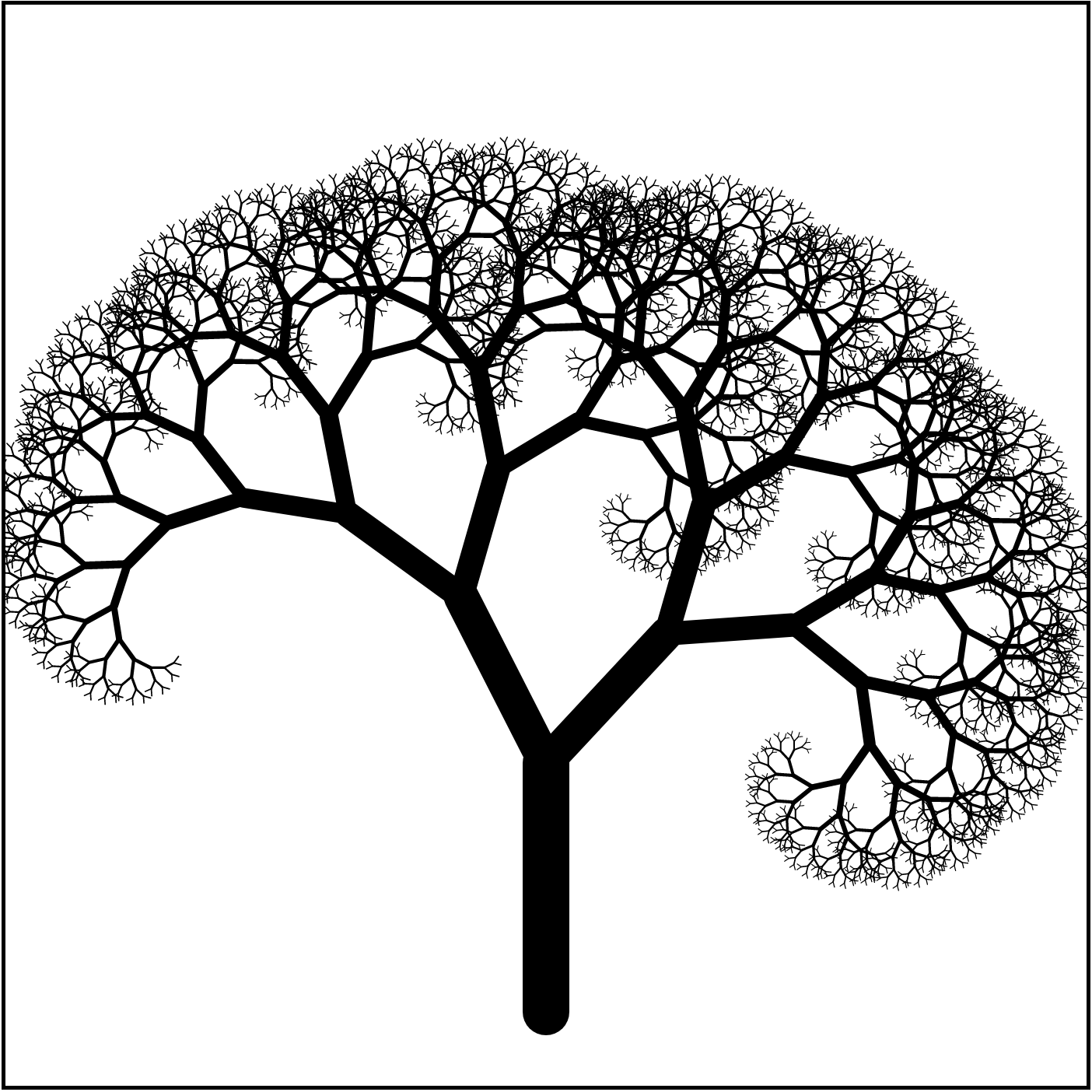
How Did I Make the Tree?

To Identify
-
Basic Shape
-
Recursive Step: transformation(s)?
Recursive Tree Demo
lec12-recursive-tree.zip
Whoa, Dude
lec12-animated-tree.zip
Assignment 07
Make a website that incorporates (recursive) self-similar graphics
- must change some attribute by recursion depth
Next Week
Automated Graph Drawing!
- Given (only) sets of vertices and edges of a graph, how can we draw it so that it looks nice?