Lecture 11: Coordinate Transformations, Recursion & Self-similarity I
COSC 225: Algorithms and Visualization
Spring, 2023
Annoucements
Assignment 06 Due Friday MONDAY!!!
- tester later this week
Outline
- Coordinates
- Coordinate Transformations
- Koch Curve Activity
- SVG Groups and Coordinates
Motivation: Self-Similarity

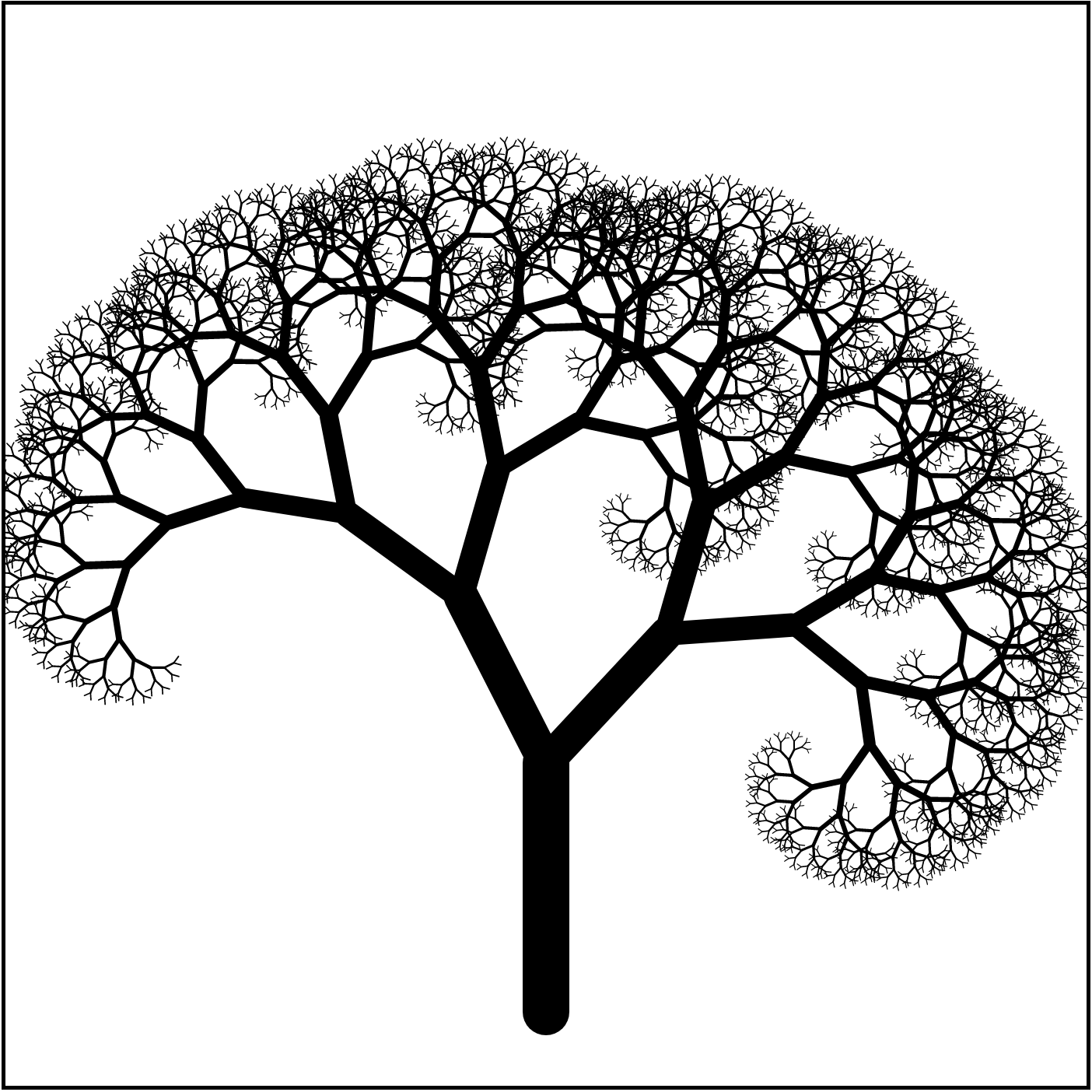
Goal
Generate self-similar graphical content
Homework 07: draw self-similar images
Coordinates
Cartessian Coordinates:
- associate each point in the plane with a pair of numbers: $A = (x, y)$
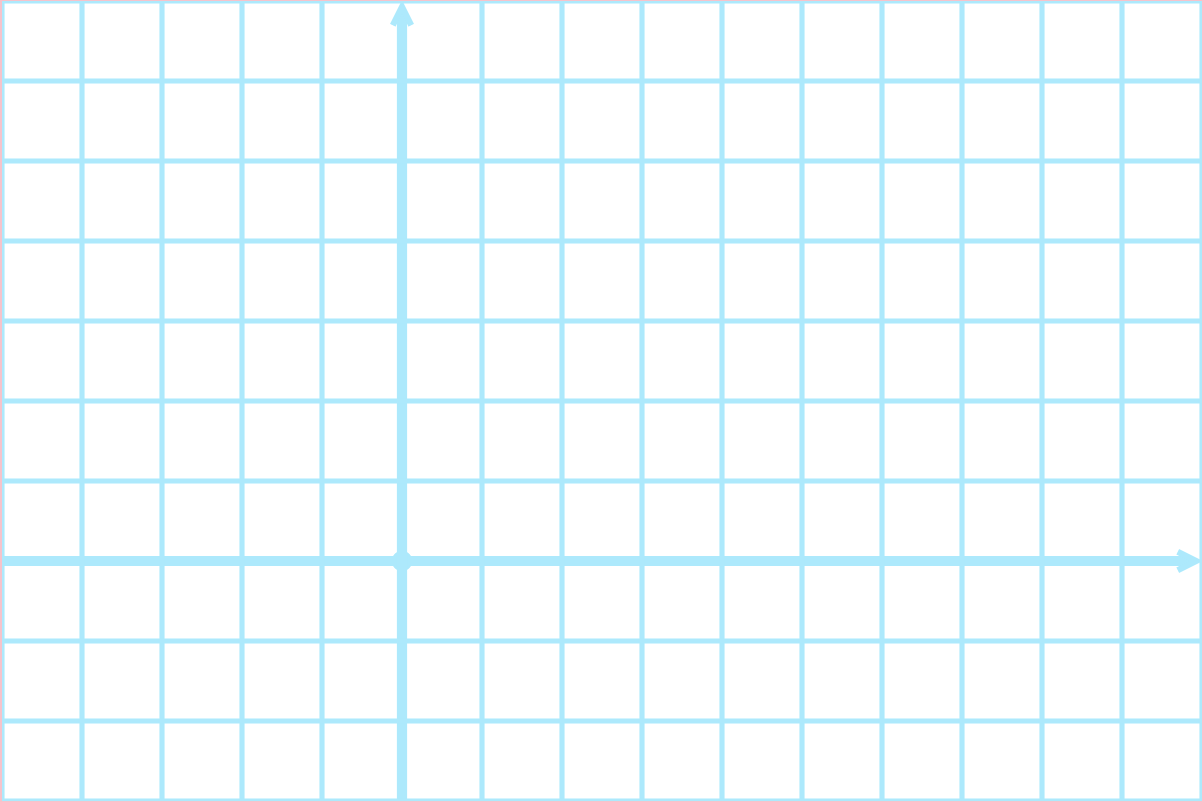
Screen vs Standard Coordinates
Screen coordinates:
- origin is upper left corner
- $x$ increases in right direction
- $y$ increases in downward direction
Standard coordinates:
- origin is somewhere
- depends on region we want to depict
- $x$ in right direction
- $y$ increases in upward direction
Today: use standard coordinates!
Points and Vectors
- a point is a location in the plane
- specified by a pair of numbers: coordinates
- a vectors is a displacement between points
- magnitude + direction
- arrows
- specified by a pair of numbers: components
Points and Vectors, Illustrated

Vector Operations
Vectors can be manipulated with algebraic operations:
- vector addition:
- $(u_1, u_2) + (v_1, v_2) = (u_1 + v_1, u_2 + v_2)$
- scalar multiplication:
- $c (u_1, u_2) = (c u_1, c u_2)$
Coordinates can be interpreted as vectors:
- associate the point $A = (x, y)$ with the vector $(x, y)$
Vector Operations Illustrated

Basic Coordinate Transformations
SVG supports transformation of elements (shapes, groups, etc)
-
translate(tx, ty): take each vector $(a, b)$ and move it to $(a + t_x, b + t_y)$ -
scale(s): take each vector $(a, b)$ and move it to $(s \cdot a, s \cdot b)$ -
rotation(d): rotate each vector by $d$ degrees in the counter clockwise direction around the origin
For example:
<rect width="20" height="20" transform="translate(30, 40)"/>
Translation
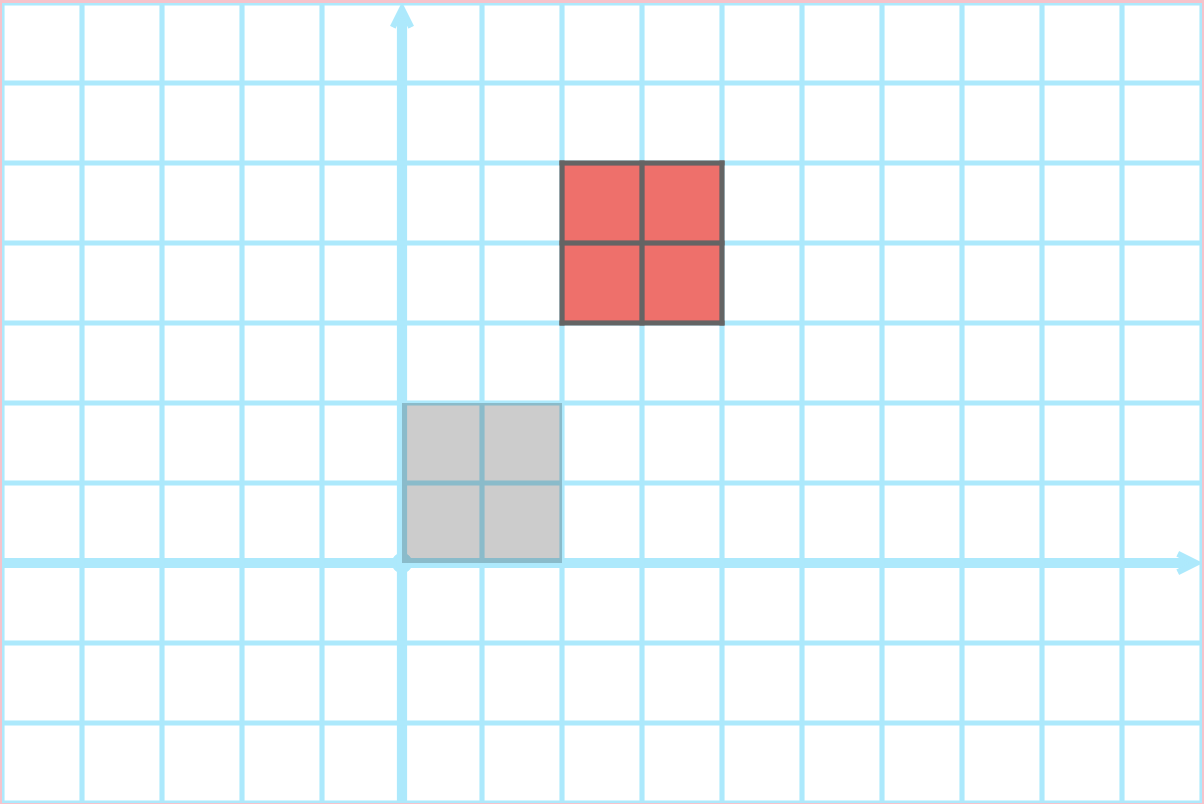
Scale
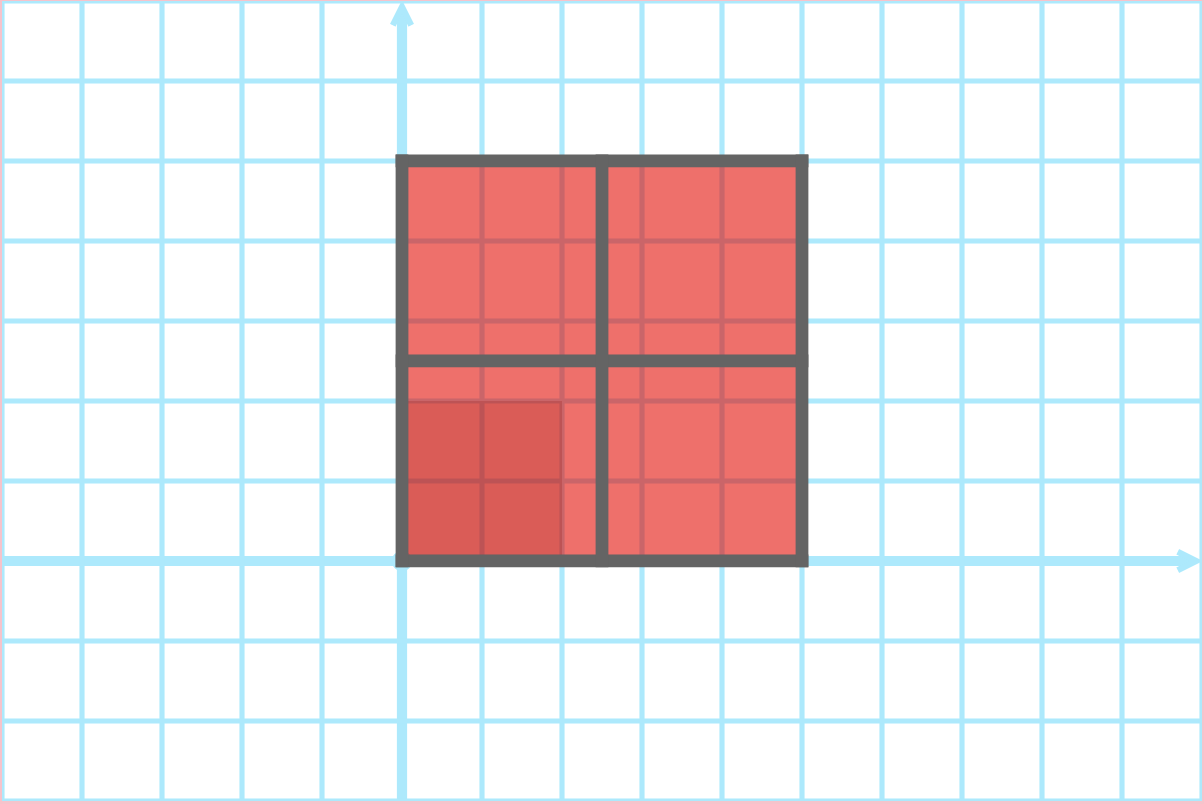
Rotation
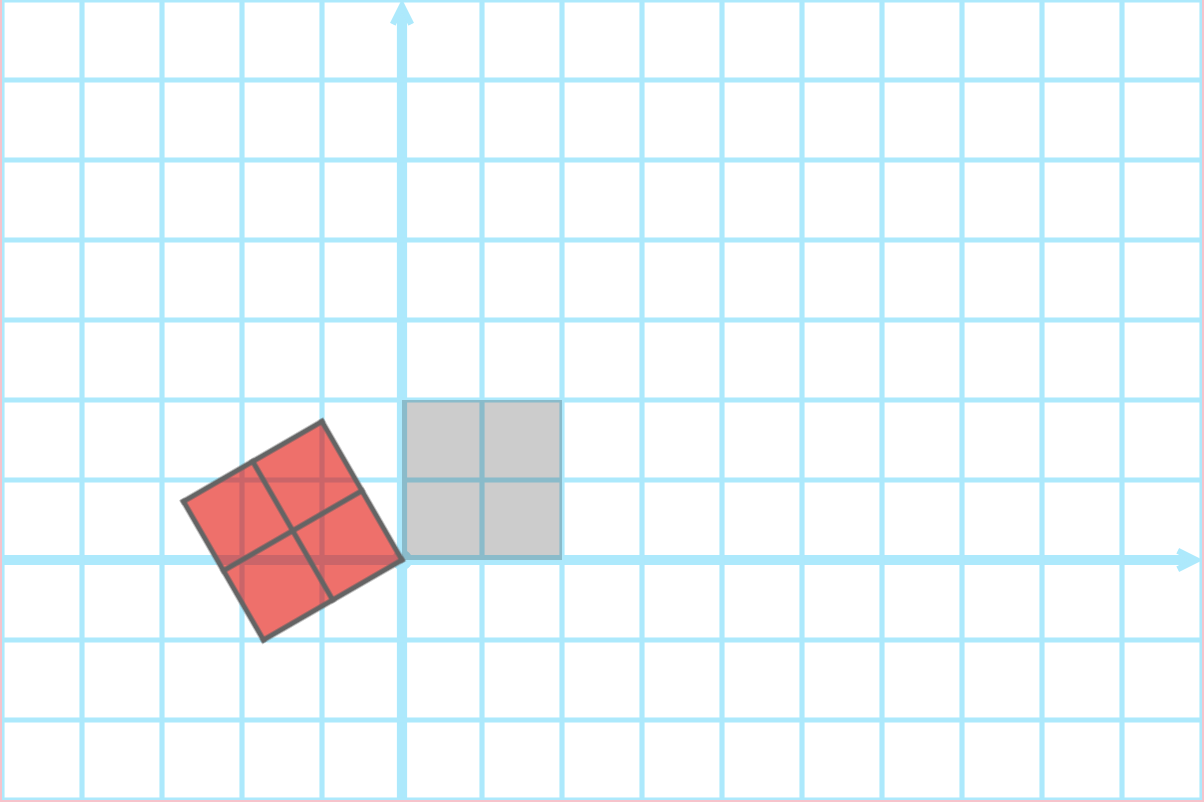
Composing Transformations
Transformations can be composed:
- perform one transformation, then another, …
- transformations are applied
- in order “left to right”
- relative to previously transformations
Translation then Rotation
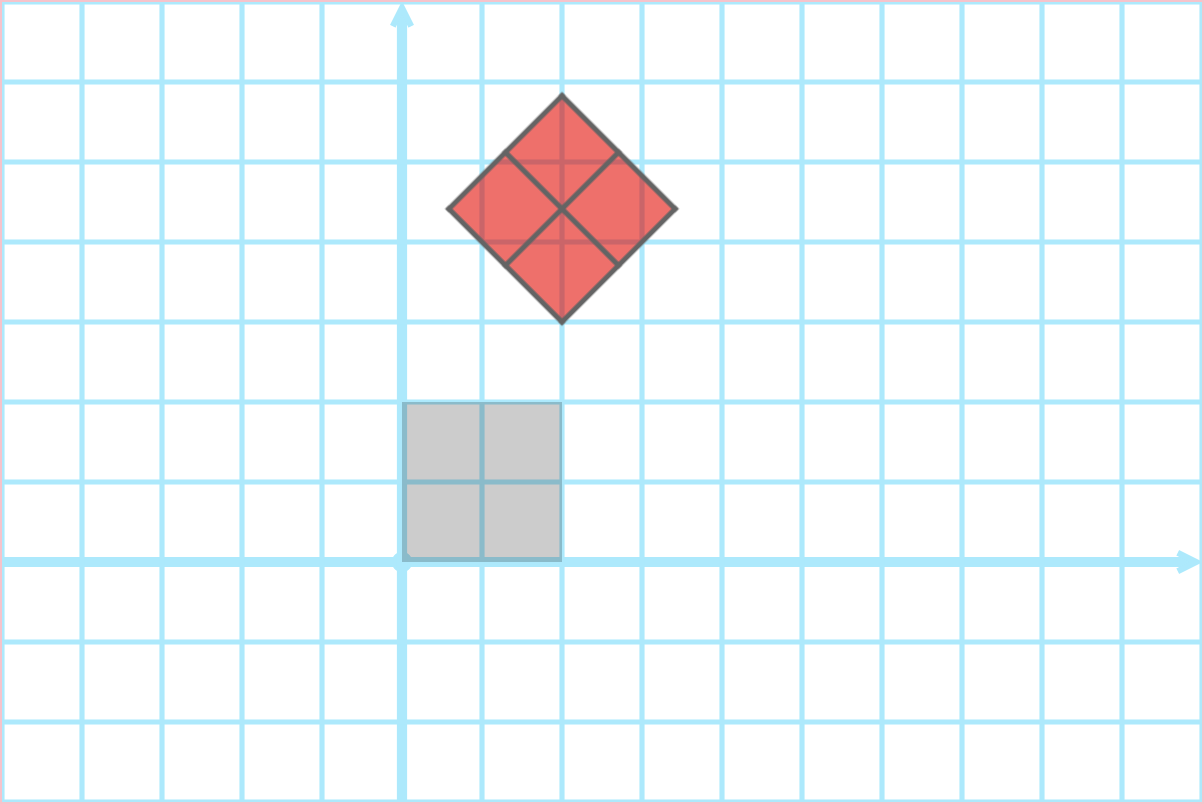
Rotation then Translation
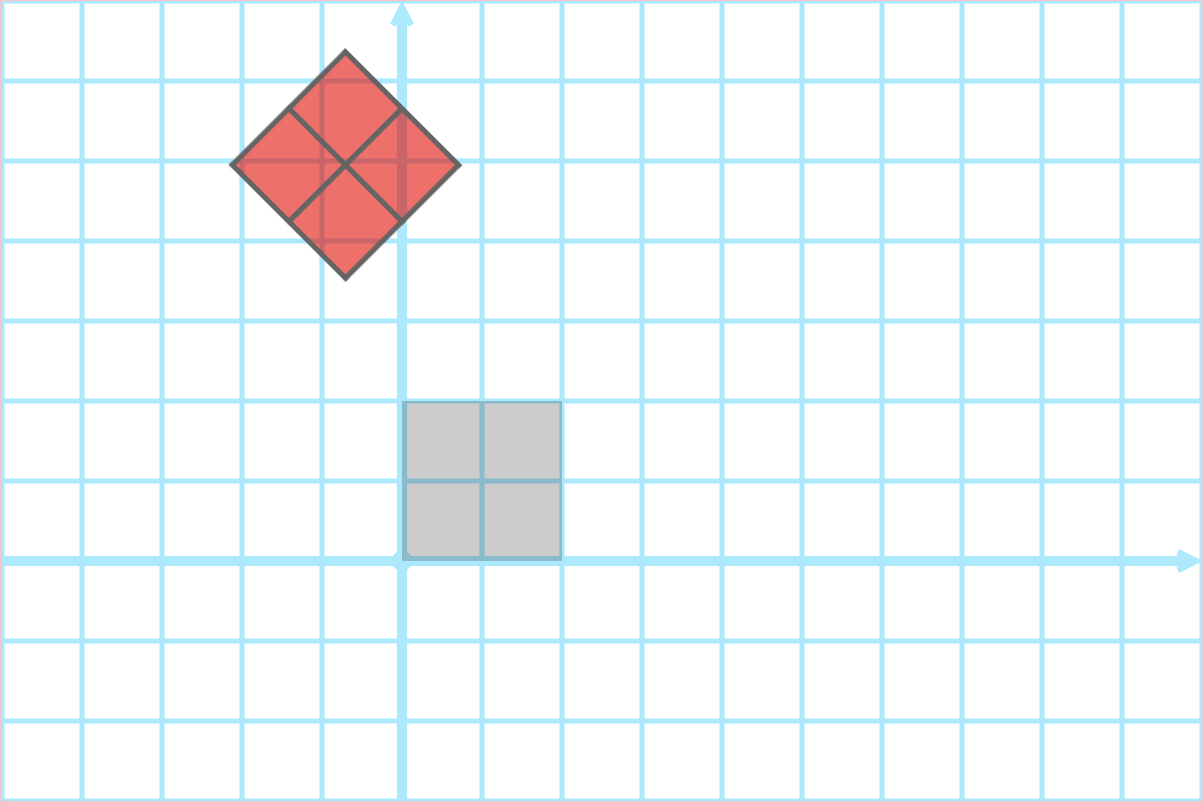
Demo
lec11-coordinate-transformations.zip
translate(-20, 10) scale(2)?

scale(2) translate(-20, 10)?

More Generally
A broad class of transformations are defined by:
- how they transform the first standard basis vector $e_1 = (1, 0)$
- how they transform the second standard basis vector $e_2 = (0, 1)$
- how they transform the origin $(0, 0)$
Affine Transformations
Suppose a transformation maps:
- vector $(1, 0)$ to $(a, b)$
- vector $(0, 1)$ to $(c, d)$
- point $(0, 0)$ to $(e, f)$
To apply transformation to $(x, y)$:
- write $(x, y) = x (1, 0) + y (0, 1)$
- apply transformation to $(1, 0)$ and $(0, 1)$
- get resulting value: $x (a, b) + y (c, d) = (ax + cy, bx + dy)$
-
add $(e, f)$ to result:
$(ax + cy + e, bx + dy + f)$
This is an affine transformation
matrix Transformations
In SVG you can perform an affine transformation
- vector $(1, 0)$ to $(a, b)$
- vector $(0, 1)$ to $(c, d)$
- point $(0, 0)$ to $(e, f)$
with
transform=matrix(a, b, c, d, e, f)
matrix transforms include all scale, translate, rotate transforms, and more!
Questions
-
What is the
matrixequivalent oftranslate(20, 30)? -
What is the
matrixequivalent ofscale(2)? -
What is the
matrixequivalent ofrotate(90)?
Question
What is the matrix of this transformation?
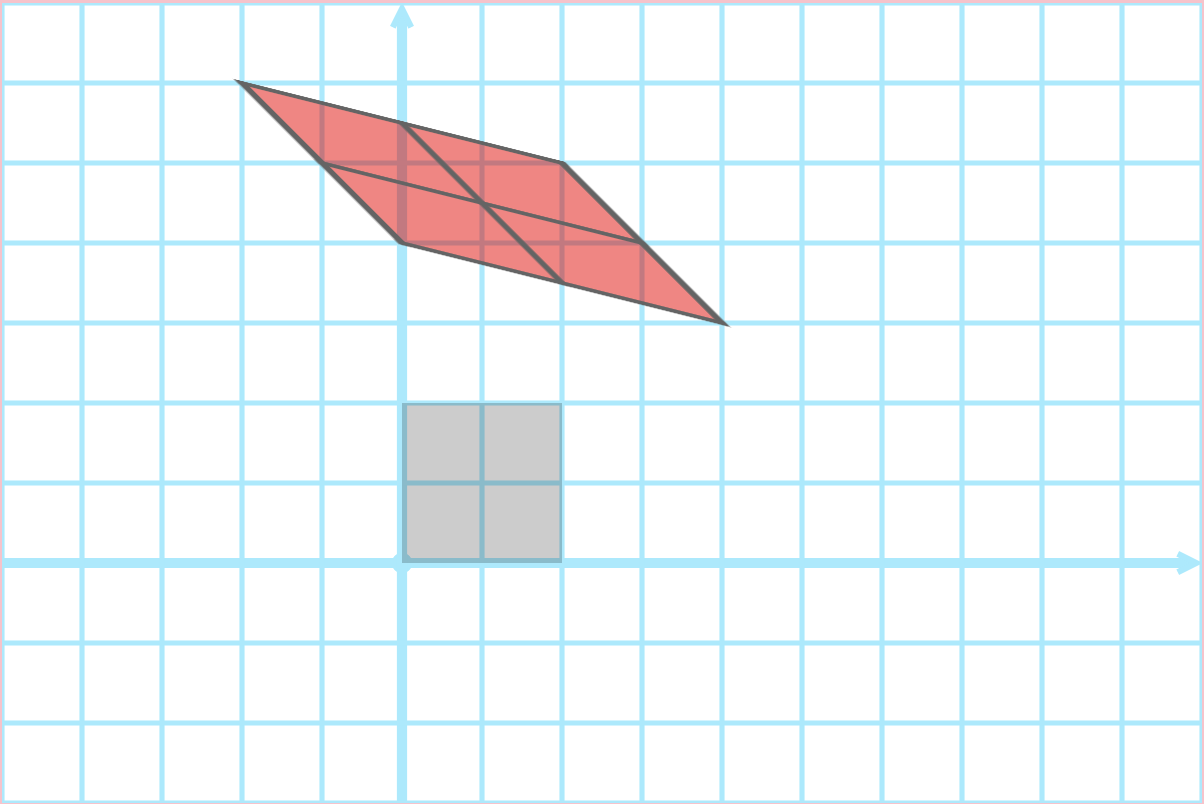
Self-Similarity via Transformations

Example: Koch Curve I
How did we make the snowflake fractal?
Step 1: define a basic shape
Example: Koch Curve II
How did we make the snowflake fractal?

Step 2: define sub-shapes for basic shape
Example: Koch Curve III
How did we make the snowflake fractal?

Step 3: recurse
Example: Koch Curve IV
How did we make the snowflake fractal?

Step 3: recurse
Observation

Each iteration draws a bunch of transformed copies of the original shape
Repetition and Transformation in SVG
-
Define the basic shape in a
<defs>element<defs> <rect id="my-rect" width="20" height="20"/> </defs> -
Draw basic shape with
<use>, applytransformto transform the element<use href="#my-rect" transform="translate(20, 30)"/>
Now can re-use my-rect over and over again with different transformations
- of course, this can (should?) all be done with JavaScript
Activity
Draw two iterations of the Koch curve!
lec11-koch-step.zip
Next Time

Make things easier!
- compose transformations by nesting group (
<g>) elements - program drawing recursively