Lecture 10: Convex Hulls; Animation

COSC 225: Algorithms and Visualization

Spring, 2023

Annoucements

Assignment 06: Submit Pair Preferecnes Today!

Outline

Convex Hulls, Finished
3 Ways to Animate!
- CSS transition property
- setInterval
- window.requestAnimationFrame

Last Time: Convex Hulls

Input:

set of points in plane
- $(x, y)$-coordinates of each point

Output:

a sequence of points $(x_1, y_1), (x_2, y_2), \ldots, (x_k, y_k)$ that define the “boundary” of the set of points
- path around $(x_1, y_1), (x_2, y_2), \ldots, (x_k, y_k)$ surrounds all points in the set in clockwise order
- the bounded region is convex

Input

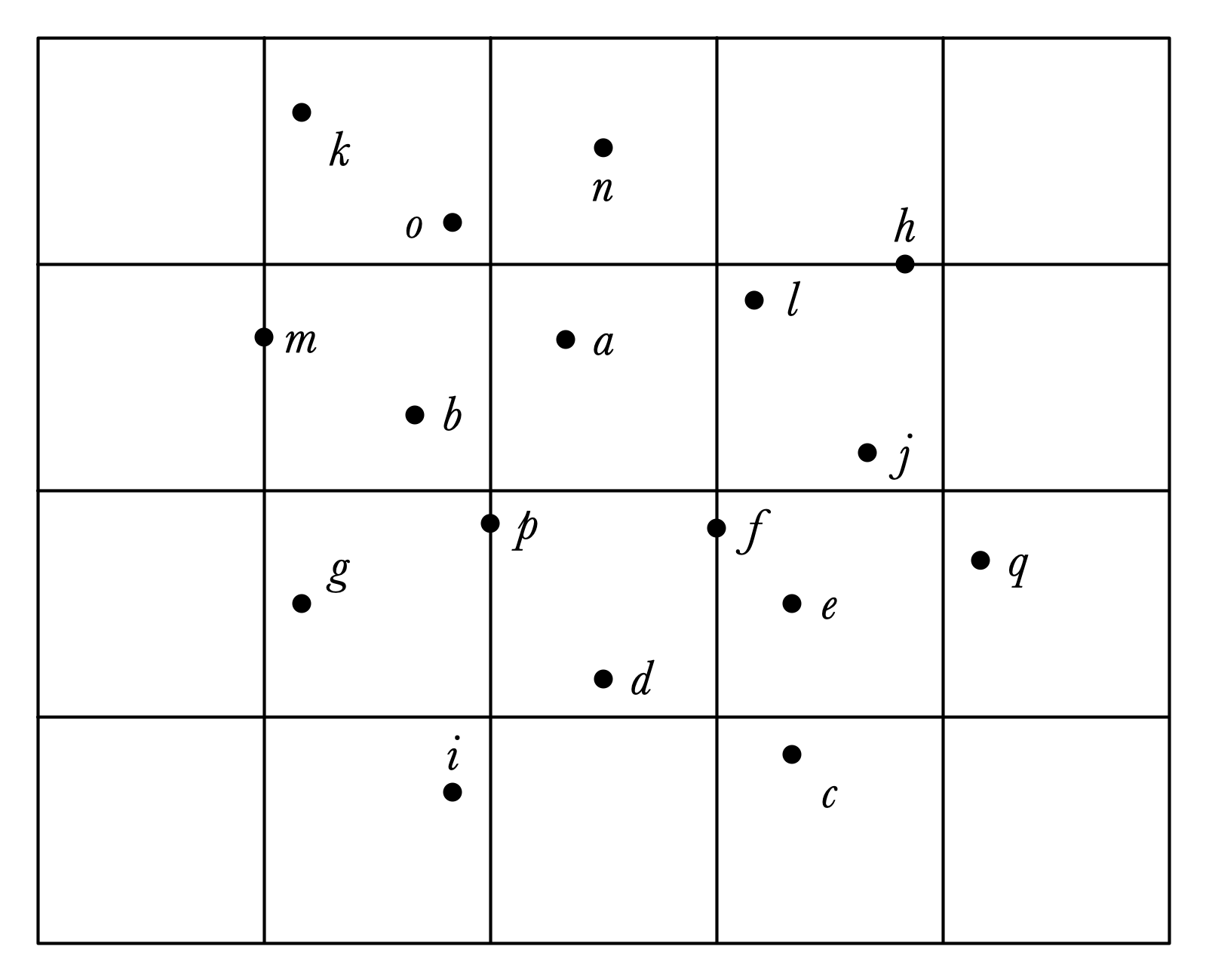
Convex Hull

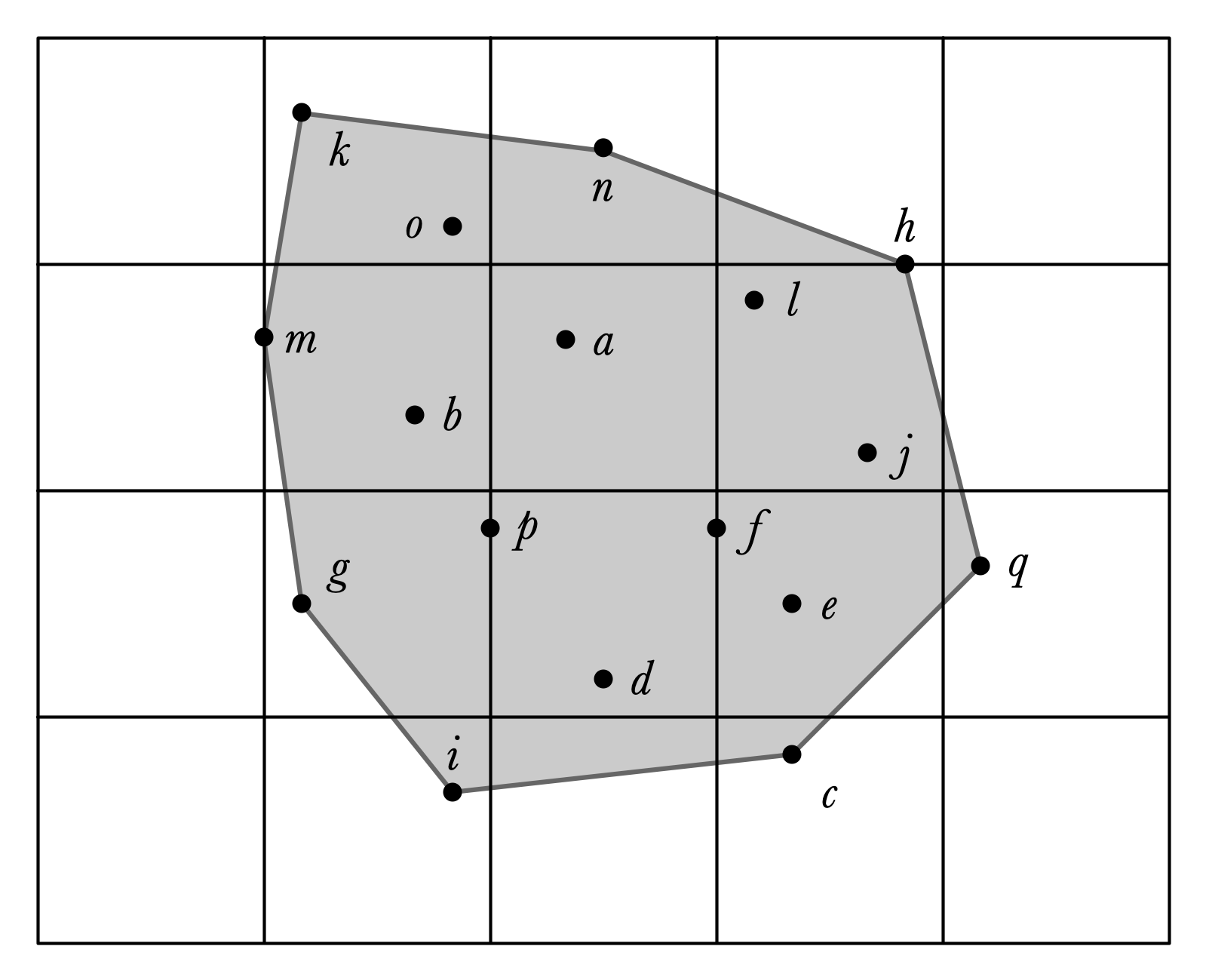
Grahm’s Scan Algorithm

Pre-process $X$ by sorting by $x$-coordinate:
Consider points one by one to determine if they are on the upper boundary of $CH(X)$
repeat process from right to left to get lower convex hull

Graham Scan Idea, Illustrated

Graham’s Scan Pseudocode

X sorted by $x$-coordinate
stk a stack, initially storing first two points in X

For each remaining C in X:

if stk.size() == 1, stk.push(C)
otherwise
- A and B are top two elements in stk
- while ABC is not a right turn and stk.size() > 1
  - stk.pop(), update A, B
- stk.push(C)

Graham Scan with a Stack

Claim

When Graham’s Scan completes, stk stores the points along the upper boundary of the convex hull of $X$.

Why?

Must show:

Sequence of points in stk make only right turns.
All points in $X$ are below path formed by points in stk

Popping Moves Boundary Up

Graham’s Scan Efficiency?

If there are $n$ points, what is the running time of Graham’s scan?

assume: stack operations are $O(1)$, “left turn” is $O(1)$

Pseudocode Again

X sorted by $x$-coordinate
stk a stack, initially storing first two points in X

For each remaining C in X:

if stk.size() == 1, stk.push(C)
otherwise
- A and B are top two elements in stk
- while ABC is not a right turn and stk.size() > 1
  - stk.pop(), update A, B
- stk.push(C)

Finishing the Computation

How to find the lower boundary of $CH(X)$?

Lower Boundary Illustrated

Assignment 06

Make an interactive visualization for Graham’s scan algorithm

user can add points in the plane
program steps through execution and illustrates each step
returns convex hull of points
separate non-interactive method for testing

Complete description coming soon!

Animation

Updated DFS Visualization

Now highlights current node.
Has an animate button

Demo!

lec10-dfs-animated.zip

Highlighted Vertex

GraphVisualizer changes

Added new SVG layer: overlayGroup
- <g></g> element for “group”
- sits “above” other layers (edges, vertices)
Methods:
- addOverlayVertex(vtx)
- moveOverlayVertex(vtx1, vtx2)
- removeOverlayVertex(vtx)

Dfs changes

create and move overlay vertex for cur vertex

A Simple Goal

Goal 1. Show motion of highlighted vertex

highlight doesn’t “jump” from one frame to the next

Simple Animation with CSS

For this animation:

only changes are to two attributes of a circle object
- cx and cy change
one-shot animation in response to change

Such things can be animated with CSS!

have class overlay-vertex

CSS Transitions

/* list the properties to apply transition to */
transition-property: cx, cy;

/* how long should transition last?*/
transition-duration: 500ms;

/* how long 
/* some options: ease (default), ease-in, ease-out, ease-in-out, linear*/
transition-timing-function: ease;

/* should we delay the start of the transition? */
transition-delay: 500ms;

Demo Animation!

A Less Simple Goal

Goal 2. Animate an entire execution of DFS without manually stepping through.

How fast should steps be?

JavaScript Timed Iteration

setInterval(method, time, arg1, ...) method:

call method with arguments arg1, ... every time ms, until eternity
returns the ID of an Interval
to stop, use clearInterval(id) method

The method is called a callback method

DFS Animation

Repeatedly call step() function until algorithm terminates

I used three methods:

animate to start the animation
animateStep to decide what to do for a single animation step
- call step() if the algorithm isn’t done
- stop the animation if it is done
stopAnimation to stop the animation

Starting the Animation

    this.animate = function () {
	if (this.curAnimation == null) {
	    this.start();
	    this.curAnimation = setInterval(() => {
		this.animateStep();
	    }, 1000);
	}
    }

Animating a Step

    this.animateStep = function () {
	if (this.active.length > 0) {
	    console.log("taking a step from vertex " 
            + this.cur.id);
	    this.step();
	} else {
	    this.stopAnimation();
	}
    }

Stopping the Animation

    this.stopAnimation = function () {
	clearInterval(this.curAnimation);
	this.curAnimation = null;
	console.log("animation completed");
    }

Demo Animation

Animation: A Third Way

lec10-bouncing-ball.zip

Goal. Animate a bunch of dots that bounce around the screen!

simple movement
indefinite animation
- no fixed start/end position

Bouncing Ball Demo

Bouncing Ball Implementation

window.requestAnimationFrame(callback):

perform operations one time, then redraw screen
- precise timing is set by system
to animate motion, must call requestAnimationFrame for each frame
- this is typically done by having callback recursively call the function making the request

Dot Animation Example

Each dot executes this code:

    this.animate = function () {
	this.updateLocation(this.cx + this.vx, this.cy + this.vy);
	if(this.cx <= 0 || this.cx >= WIDTH) {
	    this.vx = -this.vx;
	}
	if(this.cy <= 0 || this.cy >= HEIGHT) {
	    this.vy = -this.vy;
	}
	window.requestAnimationFrame(() => this.animate());
    }