Lecture 09: Convex Hulls
COSC 225: Algorithms and Visualization
Spring, 2023
Annoucements
- Office hours canceled today
- Re-submission for assignments 1 and 2 open Wednesday to Friday
- Assignment 06 can be done in pairs!
- partner questionnaire today by Wednesday
- Assignment 06 due 03/24
Outline
- Convex Hulls
- Activity: Finding the Convex Hull
- Graham’s Scan Algorithm
Last Time
Depth-first Search: A Case Study in Visualizing Algorithms
- Building a graph interactively
- Stepping through an execution
- Visualizing each step
Today
Convex hulls:
- fundamental problem in computational geometry
- topic of Assignment 06
Convex Hulls, Two Views
Given a finite set of points in the plane:
- What is the smallest convex region that contains all of the points?
- What is the minimum perimeter of a polygon that contains the points?
Visualizing Convex Hulls

Which Points are on the Boundary?

Convex Hull Problem
Input:
- set of points in plane
- $(x, y)$-coordinates of each point
Output:
- a sequence of points $(x_1, y_1), (x_2, y_2), \ldots, (x_k, y_k)$ that define the “boundary” of the set of points
- path around $(x_1, y_1), (x_2, y_2), \ldots, (x_k, y_k)$ surrounds all points in the set in clockwise order
- the bounded region is convex
Convex Hull Output Depiction

Activity!
Find the Convex Hull!
Graphed Points
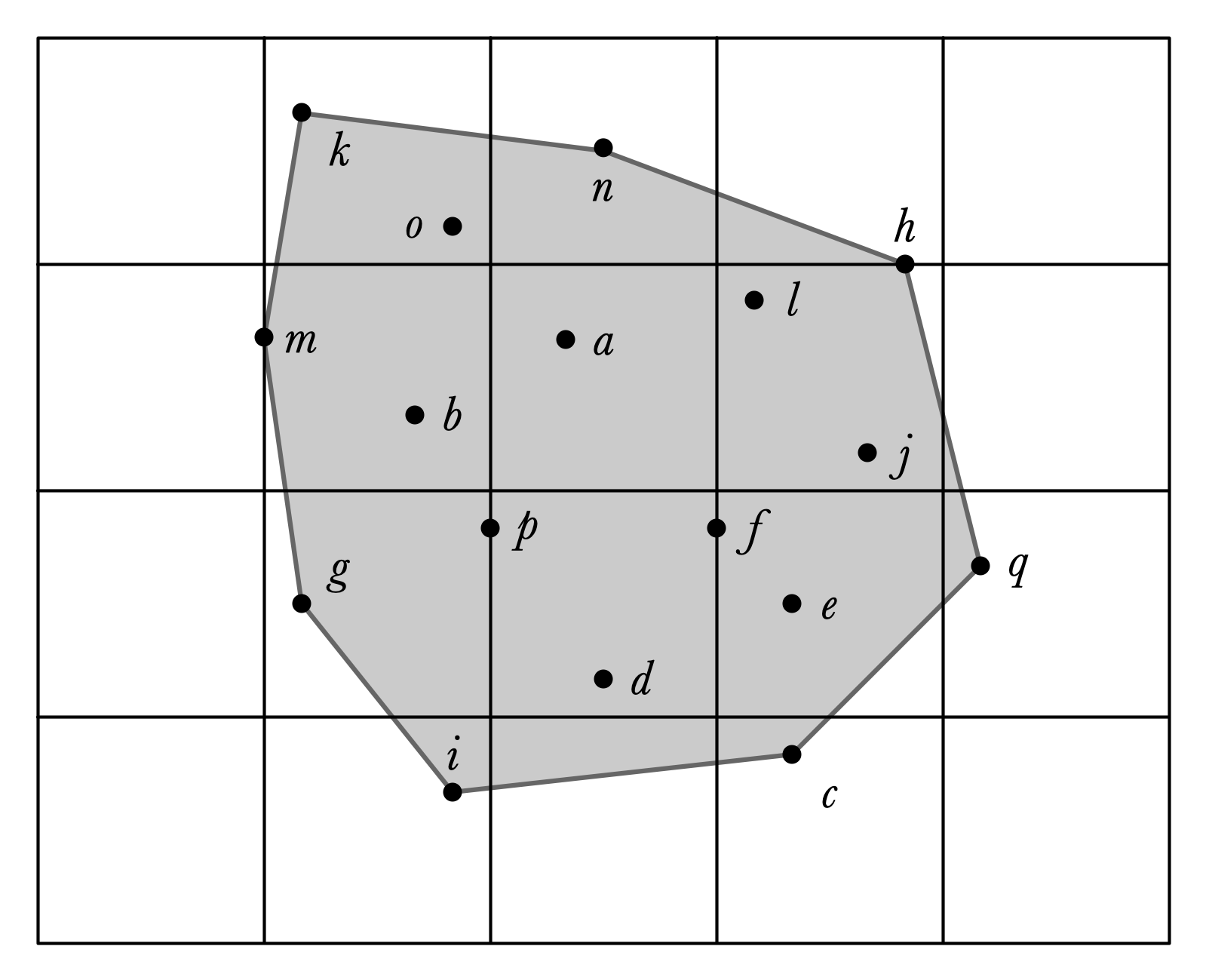
With the Convex Hull
Observe
It is easy to find by hand once you’ve graphed the points.
Question. How to program a computer to find the convex hull?
Notation
- $X = {(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)}$ a set of points
- $CH(X)$ is the convex hull of $X$
- more specifically, sequence of points in $X$ that are vertices of the convex hull in clockwise order
- start from left-most boundary point
Initial Question
Given two points $A = (x_i, y_i)$, $B = (x_j, y_j)$ in $X$, how can we determine if $AB$ is a (directed) segment of $CH(X)$?

Sub-Question
Given three points, $A, B, C$, how to determine if $C$ lies “to the right” of $AB$?

Brute-force Solution
Check all ordered pairs of points $AB$ to see if $AB$ is a segment of the convex hull!
For all $A$ and all $B \neq A$:
- check if each point $C \neq A, B$ is “to the right” of $AB$
If all $C$ are to the right of $AB$, add $AB$ to the convex hull
Efficiency?
Question. If there are $n$ points in $X$, what is the running time of the brute-force procedure?
Slight Optimization
Question. How could we ensure that we only ever check $A$ that are guaranteed to be on the convex hull?
- Hint: how can we find our first $A$ that is sure to be in $CH(X)$?
Optimization Illustration

Unfortunately
Even with the optimization, our code still takes $\Theta(n^3)$ time.
Another Approach
Try an incremental algorithm:
- Start with a set $X$ containing only one element
- in this case finding $CH(X)$ is easy!
- Add points one at a time to $X$ and update $CH(X)$ accordingly
Questions.
-
In what order should we add points?
-
How do we update $CH(X)$ in response to point additions?
Graham’s Scan Algorithm
R. Graham, 1972
First Idea
Pre-process points by sorting them by $x$-coordinate:
- process the points from left to right
Starting at left-most point, scan to the right to find upper convex hull boundary
- repeat process from right to left to get lower convex hull
Graham Scan Idea, Illustrated

How to Formalize/Implement?
Assume $X$ is an array of points, sorted by $x$-coordinate
-
How to keep track of points in $CH(X)$ (so far)?
-
How to update in response to next point?
Graham’s Scan Pseudocode
-
Xsorted by $x$-coordinate -
stka stack, initially storing first two points inX
For each remaining C in X:
- if
stk.size() == 1,stk.push(C) - otherwise
-
AandBare top two elements instk - while
ABCis not a right turn andstk.size() > 1-
stk.pop(), updateA,B
-
stk.push(C)
-
Claim
When Graham’s Scan completes, stk stores the points along the upper boundary of the convex hull of $X$.
Why?
Must show:
- Sequence of points in
stkmake only right turns. - All points in $X$ are below path formed by points in
stk
Graham’s Scan Efficiency?
If there are $n$ points, what is the running time of Graham’s scan?
Finishing the Computation
How to find the lower boundary of $CH(X)$?
Assignment 06
Make an interactive visualization for Graham’s scan algorithm
- user can add points in the plane
- program steps through execution and illustrates each step
- returns convex hull of points