Lecture 33: More Reductions, Hard Decisions
COSC 311 Algorithms, Fall 2022
Announcement
Job Candidate Talk TODAY
Victoria Dean, Carnegie Mellon University
Bridging Reinforcement Learning and Robotics: Efficient Training and Shared Evaluation
- 4:00 in SCCE A131
- Refreshments at 3:30 in SCCE C209
Remaining Coursework
- Lecture Ticket for Monday (posted today)
- Homework 6 due Next Friday (posted this weekend)
- Final Exam: Friday Dec. 16
- official announcement next week
Today
- Independent Sets and Vertex Covers
- Decision Problems and Reductions
- Hard Decision Problems?
Last Time
-
Coarse notion of efficiency:
- an algorithm is polynomial time if its worst-case running time is $O(N^c)$ for some constant $c$, $N = $ input size
-
Notion of reduction
- transform instances of problem $A$ to instances of problem $B$
- solution to $B$ reveals solution to $A$
Application. Maximum Bipartite Matching
- solved via reduction to Maximum Flow
Today
- Independent Sets & Vertex Covers
- Decision Problems
- Easy and Hard Decision Problems
Virus Protection
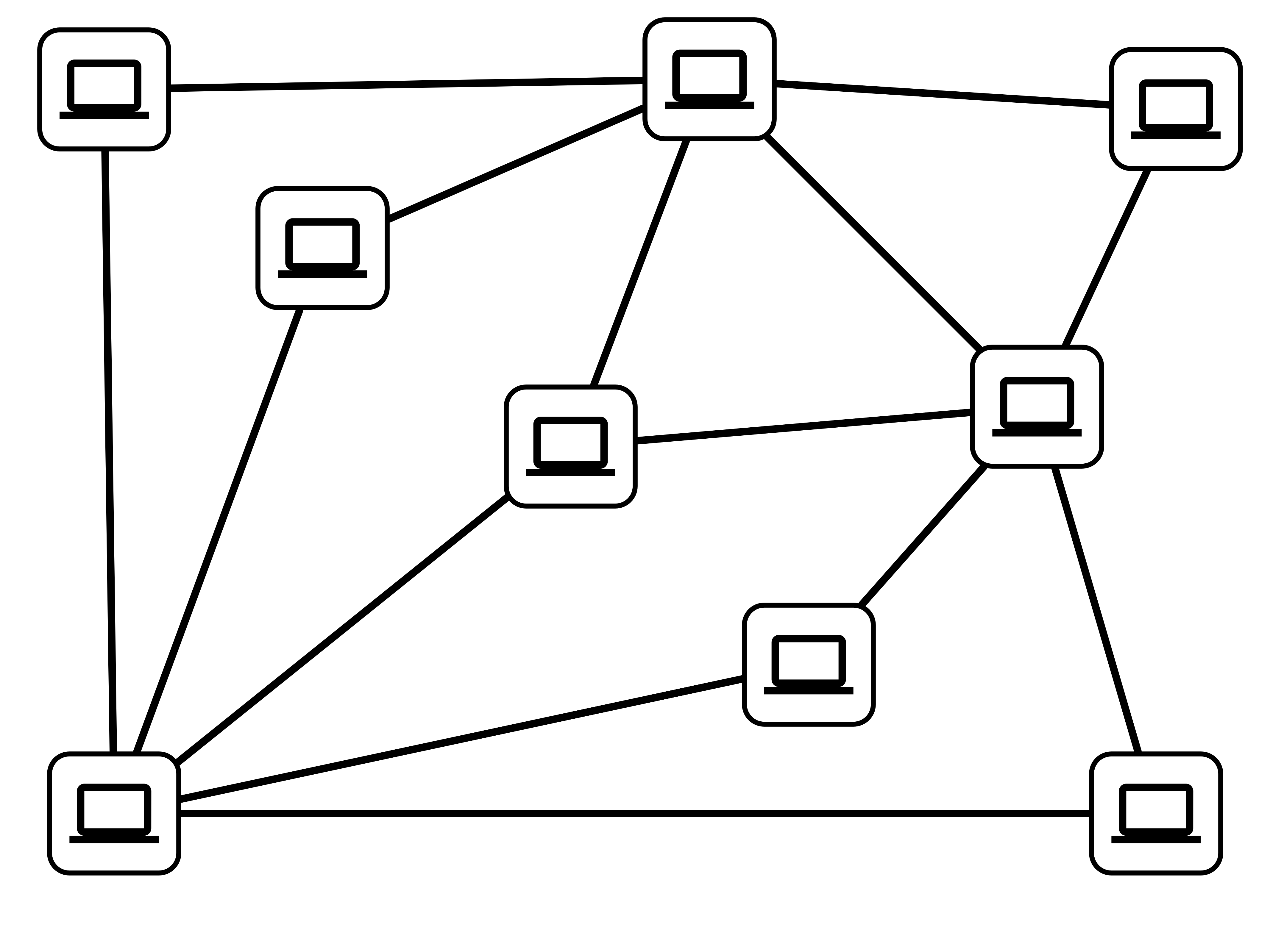
Task: Install virus protection software on computers in a network
- if two computers are connected, at least one endpoint must be protected
- software licenses are expensive!
Goal: Install software on as few computers as possible while protecting the network
Virus Protection Example
Minimum Vertex Cover (MVC)
Input:
- Graph $G = (V, E)$
Output:
- A vertex cover $C = \{v_1, v_2, \ldots, v_k\}$
- every edge $e = (u, v) \in E$ has $u \in C$ or $v \in C$
- $C$ is a vertex cover of minimal size
- there is no vertex cover of size $\ell \leq k$
Firmware Upgrade
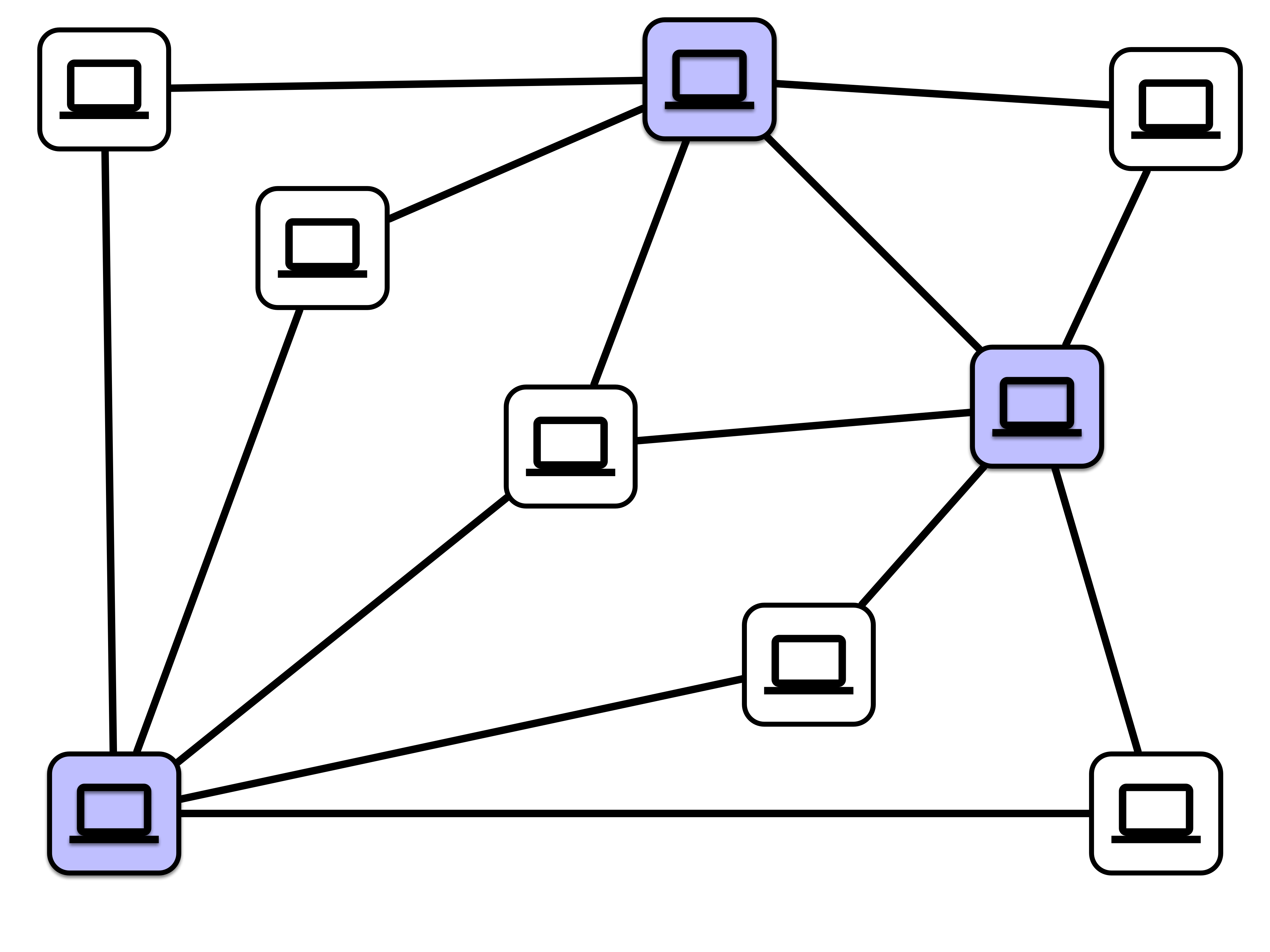
Task: Update firmware on computers in a network
- if two adjacent computers get updated, network connection between them must be manually reset
- resetting a network connection is annoying!
Goal: Update firmware on as many computers as possible without having to reset any network connections
Firmware Upgrade Example

Maximum Independent Set (MaxIS)
Input:
- Graph $G = (V, E)$
Output:
- An independent set $I = \{v_1, v_2, \ldots, v_k\}$
- there is no edge between any pair of vertices in $I$
- $I$ is an indpendent set of maximum size
- there is no independent set with $\ell > k$ vertices in $G$
Current State
-
There is no known efficient (polynomial time) algorithm for solving MVC or MaxIS
-
There is no known proof that MVC or MaxIS cannot be solved in polynomial time
Relationship Between MVC and MaxIS?
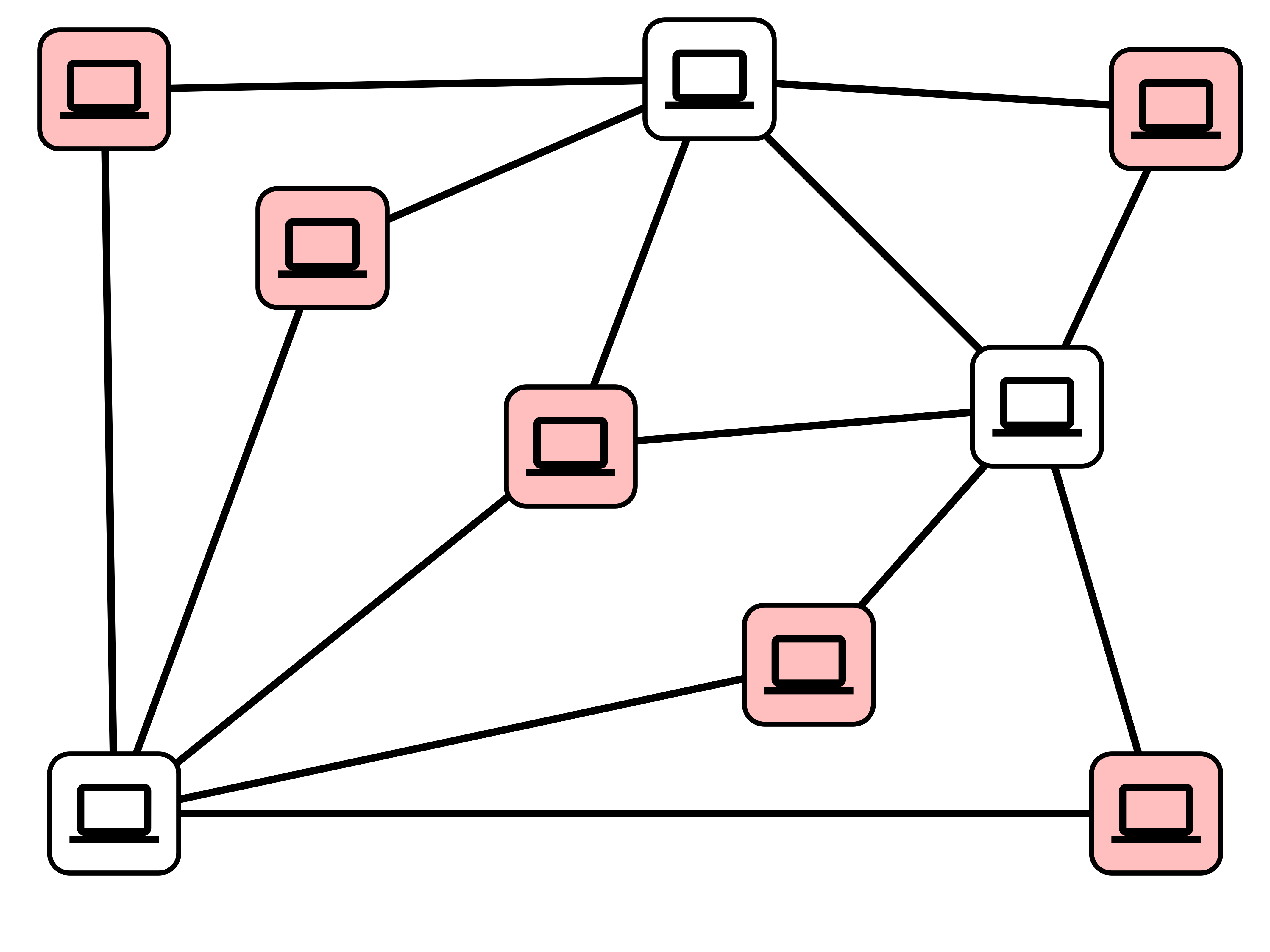
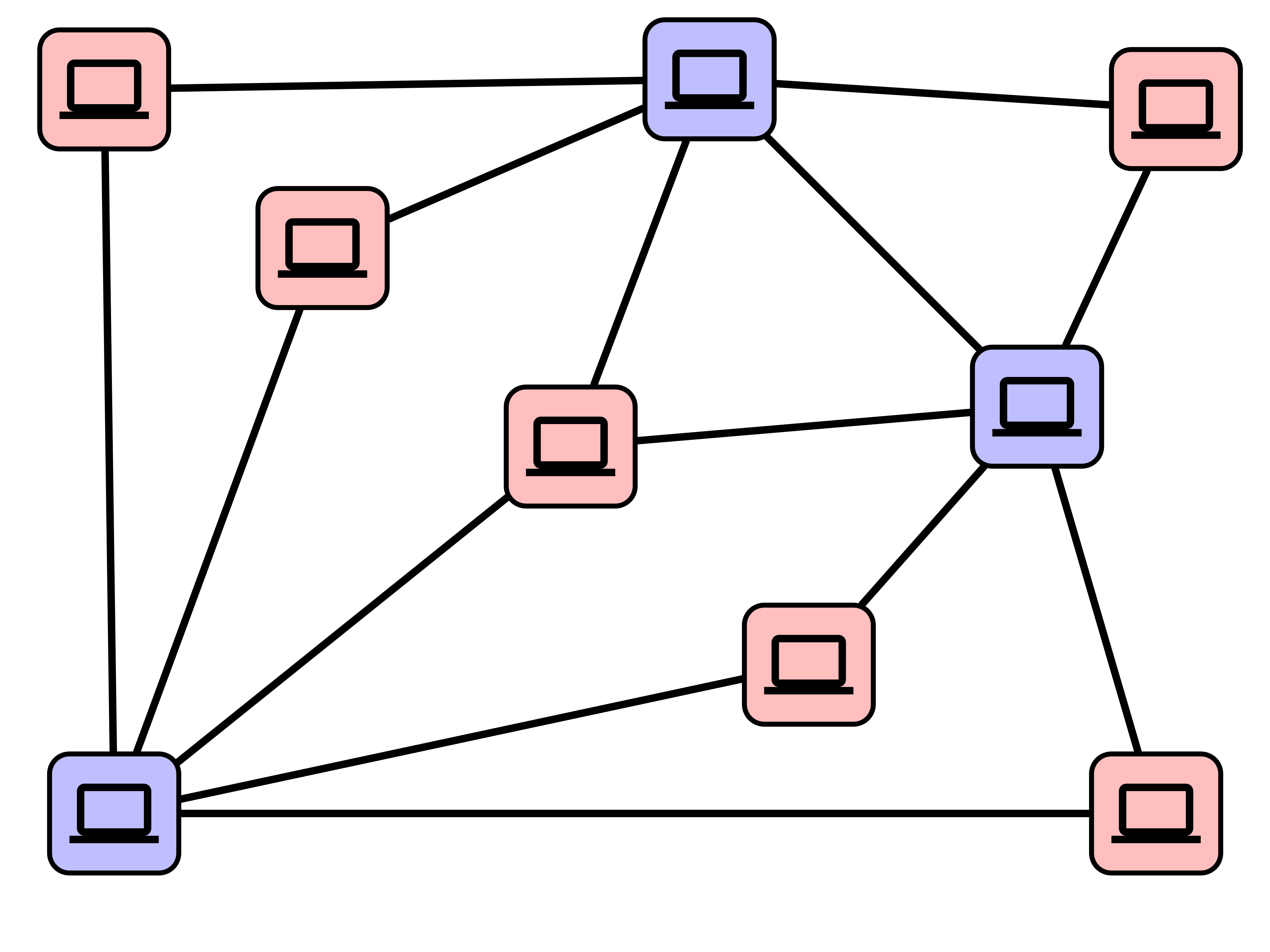
Complementary Sets
Claim 1
Suppose $G$ has a vertex cover $C$ of size $k$. Then $G$ has an indpendent set of size $n - k$, namely $V - C$.
Claim 2
Suppose $G$ has an independent set $I$ of size $k$. Then $G$ has a vertex cover of size $n-k$, namely $V - I$
Reduciblity Reminder
A polynomial time reduction from problem $A$ to problem $B$ consists of
- a polynomial time procedure to transform instances of $A$ to instances of $B$
- a polynomial time procedure to transform corresponding solutions to $B$ to solutions to $A$
If there is a polynomial time reduction from $A$ to $B$, then we write $A \leq_P B$.
Reducing MVC to MaxIS
Claim. MVC $\leq_P$ MaxIS.
Reducing MaxIS to MVC
Claim. MaxIS $\leq_P$ MVC.
Consequences
-
If we find an efficient algorithm for MVC, then we automatically get an efficient algorithm for MaxIS
-
If we find an efficient algorithm for MaxIS, then we automatically get an efficient algorithm for MVC
-
If we prove there is no efficient algorithm for MVC, then there is no efficient algorithm for MaxIS
-
If we prove there is no efficient algorithm for MaxIS, then there is no efficient algorithm for MVC
One More Technicality
Objective. Understand relationships between computational problems.
Technical issue. Desired outputs for different problems can be vastly different:
- matching
- independent set
- spanning tree
- …
Convenience. Focus on decision problems:
- output is “yes”/”no”
MVC vs VC
Minimum Vertex Cover (MVC)
-
Input: Graph $G$
-
Output: A vertex cover $C$ of smallest possible size
Vertex Cover (VC)
Input: Graph $G$, number $k$
Output:
- “yes” if $G$ has a vertex cover of size $k$
- “no” otherwise
MaxIS vs IS
Maximum Independent Set (MaxIS)
Input: Graph $G$
Output: an indpendent set of the largest possible size
Independent Set (IS)
Input: Graph $G$, number $k$
Output:
- “yes” if $G$ has an indpendent set of size $k$
- “no” otherwise
Exercise (last HW assignment)
Given an algorithm for the decision problem, devise an algorithm for the original problem.
Reductions between VC and IS
Complexity of Decision Problems
Goal. Classify (decision) problems according to their relative complexities:
- which problems can be solved efficiently?
- which problems cannot be solved efficiently?
- which problems can be reduced to other problems?
Complexity Landscape
- P = decision problems that can be solved in polynomial time $O(N^c)$ (some constant $c$)
- EXP = decision problems can be solved in time $O(2^{N^c})$ (some constant $c$)
Surprising Answer
IS and VC belong to a huge class of natural/practical problems such that
- none is known to admit a polynomial time algorithm
- a polynomial time algorithm for one would imply a polynomial time algorithm for all others
- a proof that any one cannot be solved in polynomial time would imply that none can be solved in polynomial time
The class of problems is called NP Complete
Next Time
- Boolean satisfiability (lecture ticket)
- Definition of NP
- NP completeness