Lecture 31: Stable Matchings
COSC 311 Algorithms, Fall 2022
Overview
- Stable Marriage Problem
- Gale-Shapley Algorithm
- Different Perspectives
- my research
Internship Assignment Problem
It is internship application season!
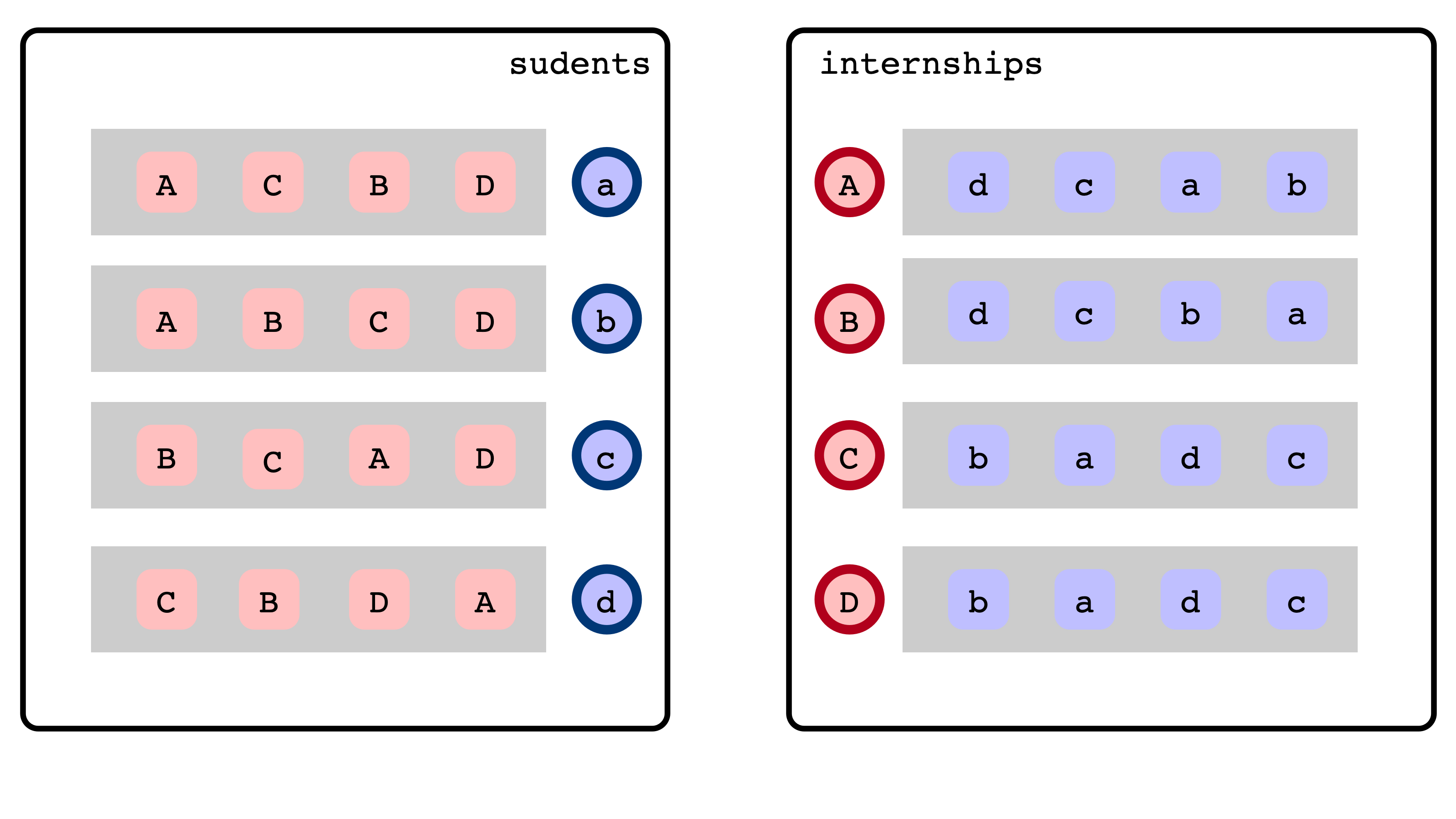
In a small world…
- Four students: $a, b, c, d$
- Four internships: $A, B, C, D$
Question. How should we assign students to internships?
Preferences
Agents have preferences in the form of a strict ranking of alternatives
- each student ranks available internships
- each internship ranks available students
Question
How do we decide whether a matching “respects” agents’ preferences?

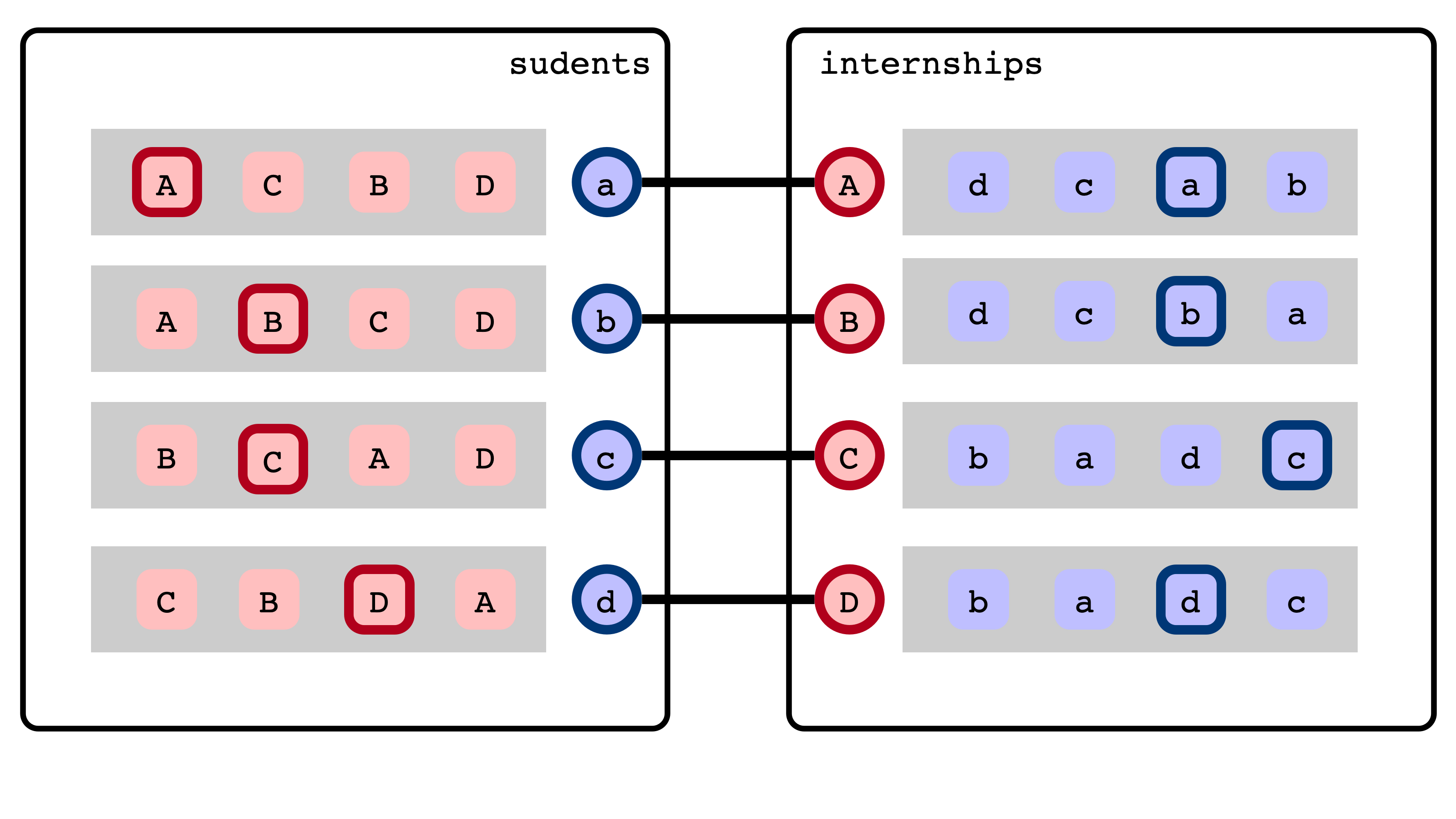
Blocking Pairs and Stability
Given:
- students, internships, preferences
- matching $M$
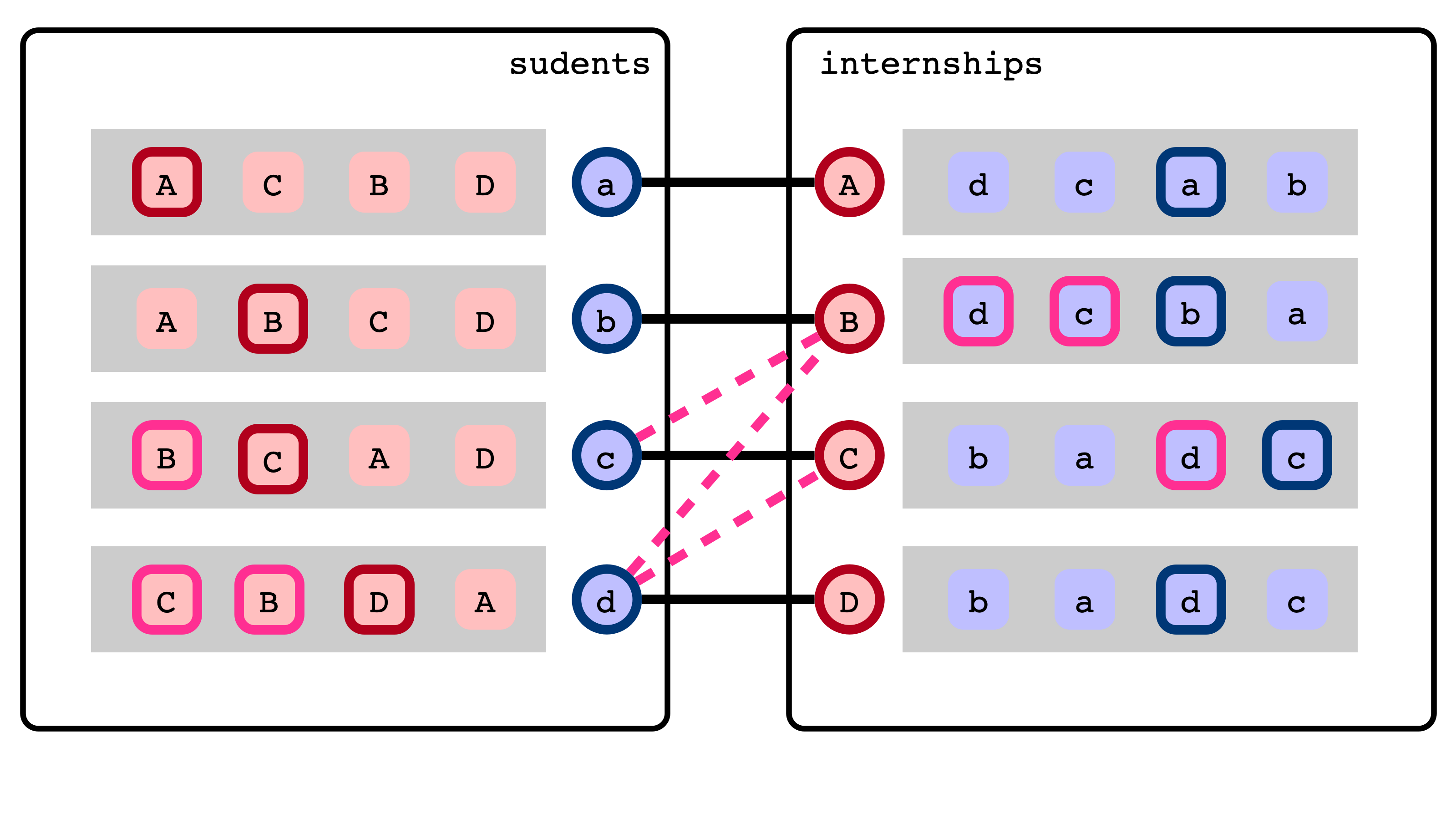
We say $(s, t)$ is a blocking pair if
- $s$ and $t$ are not matched with each other
- $s$ prefers $t$ to assigned internship in $M$
- $t$ prefers $s$ to assigned student in $M$
Blocking Pair Illustration
Blocking Pair Illustration
Stable Marriage Problem
Gale-Shapley 1962
Input:
- set of $n$ students
- set of $n$ interships
- for each student $s$, preference list ranking all internships
- for each internship $t$, preference list ranking all students
Output:
- a matching $M$ between students and internships
- $M$ is stable
- there are no blocking pairs
Questions
- Do stable matchings always exist?
- are there sets of preference lists for which there is no stable matching?
- How can we find a stable matching (if one does exist)?
Answer
Theorem (Gale-Shapley 1962). Yes! Stable matchings always exist, and there is an efficient algorithm to find one.
Gale-Shapley, Illustrated
Gale-Shapley Pseudocode
- initially, all students/internships unmatched
- while some student is unmatched
- for each unmatched student $s$,
- $s$ applies to next favorite internship
- for each internship $t$
- $t$ defers best applicant so far, rejects others
- rejected students unmatch
- for each unmatched student $s$,
Observations
- Students apply sequentially in decreasing order of preference
- $s$ only applies to $t$ after $s$ has been rejected by all preferred internships
- For each internship, deferred candidates are increasingly preferred
- Once an internship receives an application, it stays matched
Termination
Claim 1. Gale-Shapley terminates after at most $n (n - 1) + 1$ applications.
Stability
Claim 2. When Gale-Shapley terminates, the resulting matching is stable.
Conclusion
Theorem (Gale-Shapley, 1962). Every instance of the stable marriage problem admits a stable matching. If there are $n$ students and internships, a stable matching can be found in $O(n^2)$ time.
Influence and Applications
- Introduced stability as key concept in economics
- 8,000+ papers spanning econ/cs/math
- 2012 Nobel Prize in economics (Roth and Shapley)
- stable allocations and mechanism design
- Applications:
- matching med students with residencies
- content delivery networks
- kidney exchanges (variant)
Influence on My Research
Stable matchings in a decentralized setting
- Each agent is own computational entity
- Agents must communicate in order
Question 1
Is it reasonable to assume all agents explicitly know their own preferences?
Other Mechanisms
Do not assume preferences are explicitly known:
- match-maker interacts with agents by performing queries
- a query is simply a yes/no (Boolean) function about preferences
- e.g., “Would you prefer to work for a large company, or a small company?”
- match maker performs queries until enough information about preferences is elicited to determine a stable matching
- like “20 Questions”
Note. Gale-Shapley can be implemented with $O(n^2 \log n)$ queries.
A Result
Theorem (Gonczarowski, Nisan, Ostrovsky, R–). Any mechanism that finds or verifies a stable matching uses $\Omega(n^2)$ queries in the worst case.
- finding/verifying stable matchings reveals a significant amount of information about preferences
- running time of Gale-Shapley is optimal, up to $\log n$ factor
Further Implications
Finding “almost stable” matchings also requires $\Omega(n^2)$ queries.
-
“early binding commitments” either lead to
- instability
- unraveling
The Morals
- Social/political/biological/… problems can be viewed through the lense of algorithms
- Algorithmic methods and complexity measures can yield insights into natural measures of efficiency and quality of solutions
- Such investigation can give quantitative explanation to qualitative behavior
- Theorems are imporant
After the Break
Reductions and NP-completeness
To what extent can we show that a problem cannot be solved efficiently?