Lecture 30: Network Flow III

$ \def\opt{ {\mathrm{opt}} } \def\val{ {\mathrm{val}} } \def\capacity{ {\mathrm{cap}} } $

COSC 311 Algorithms, Fall 2022

Annoucement

Midterm II on Wednesday

• Practice solutions coming soon

Last Time

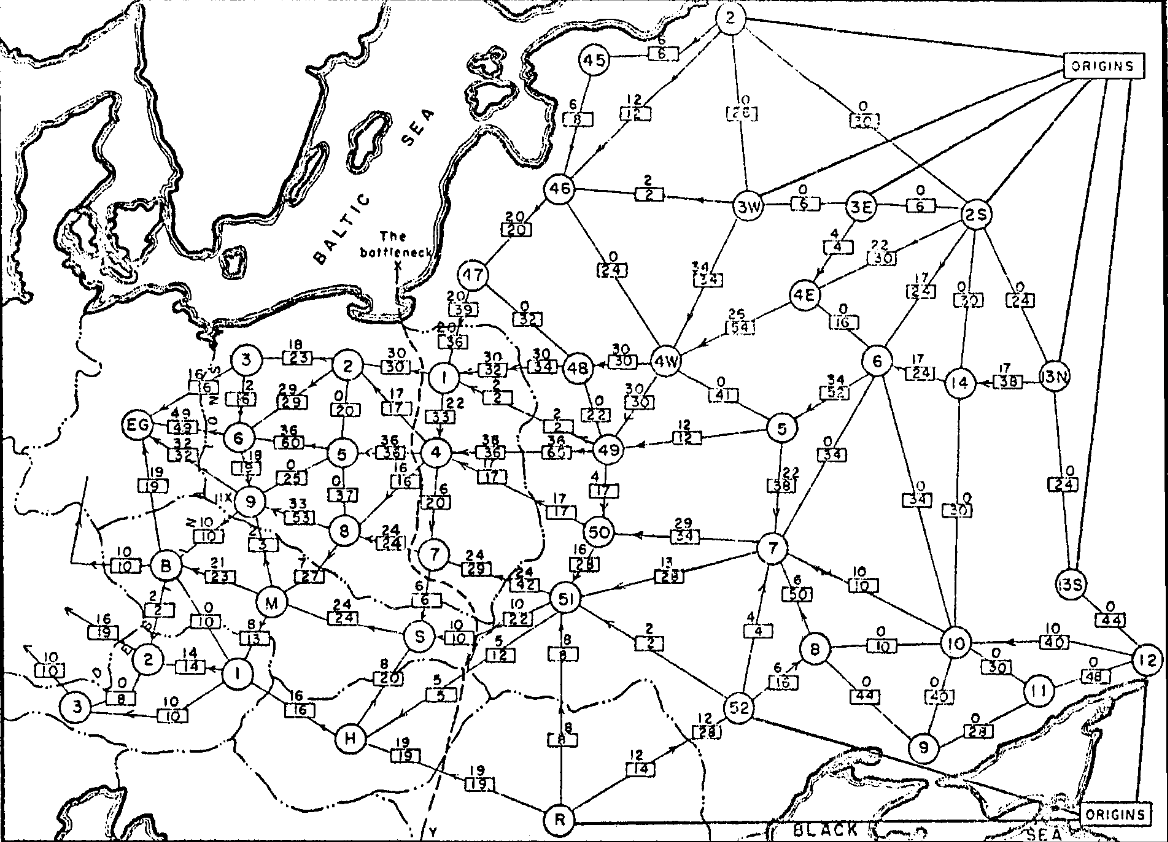
Max Flow Problem:

Input.

• weighted directed graph $G = (V, E)$
  • weights = edge capacities $> 0$
• source $s$, sink $t$
  • all edges oriented out of $s$
  • all edges oriented into $t$

Output.

• flow $f$ of maximum value
  • $\val(f) = \sum_{s \to v} f(s, v)$

We Showed

Greedy strategy doesn’t always work

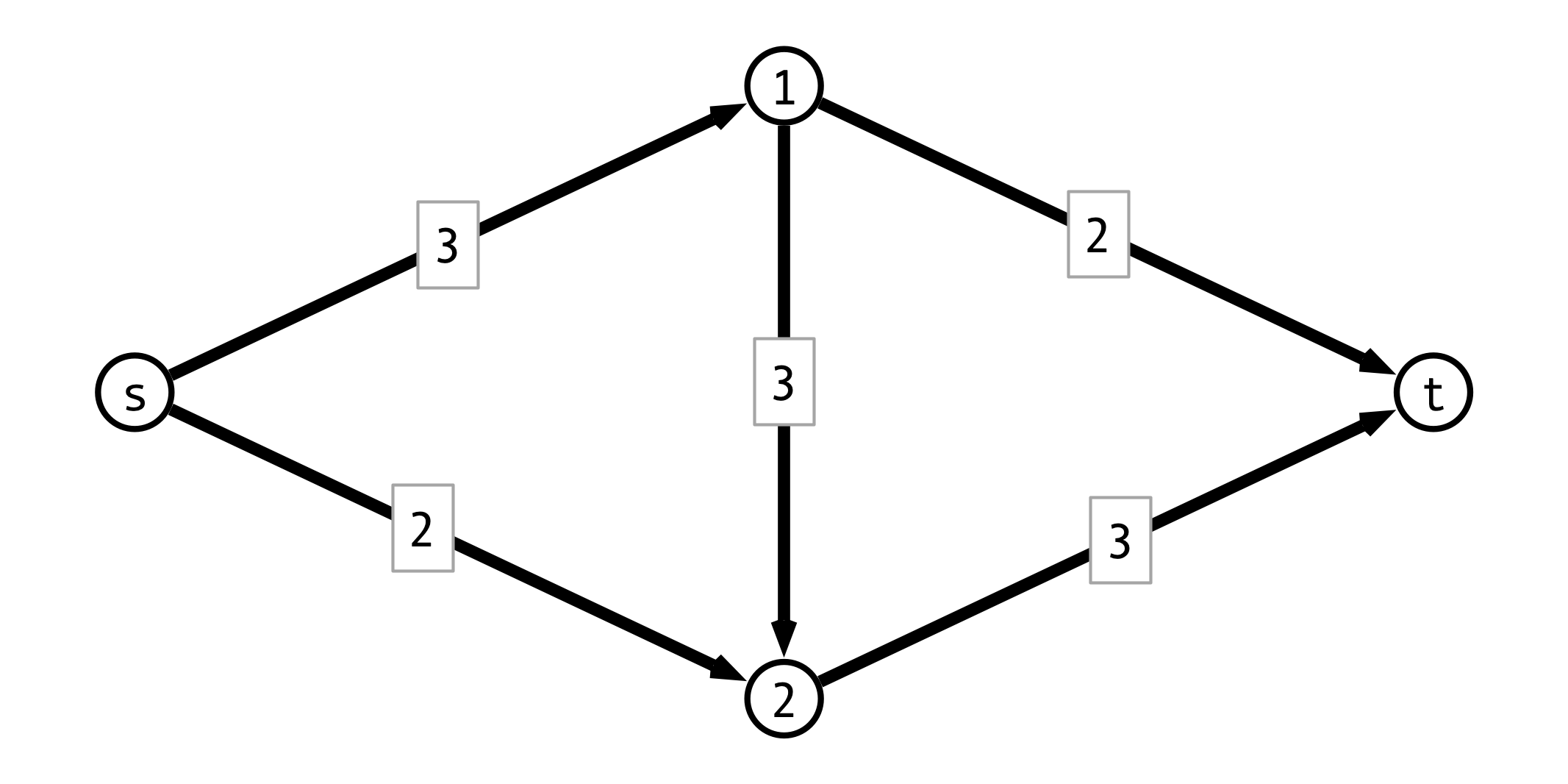
Ford-Fulkerson Idea

Given a flow $f$:

• allow forward flow to be “undone”
• when routing forward flow $f(u, v)$ across edge $(u, v)$, create backwards edge $(v, u)$ with capacity $f(u, v)$
  • graph with backwards edges = residual graph
• backwards flow cancels out forward flow

Ford-Fulkerson Algorithm:

1. apply greedy strategy to residual graph
2. update residual graph with new flow
3. continue until no unsaturated path from $s$ to $t$ remains

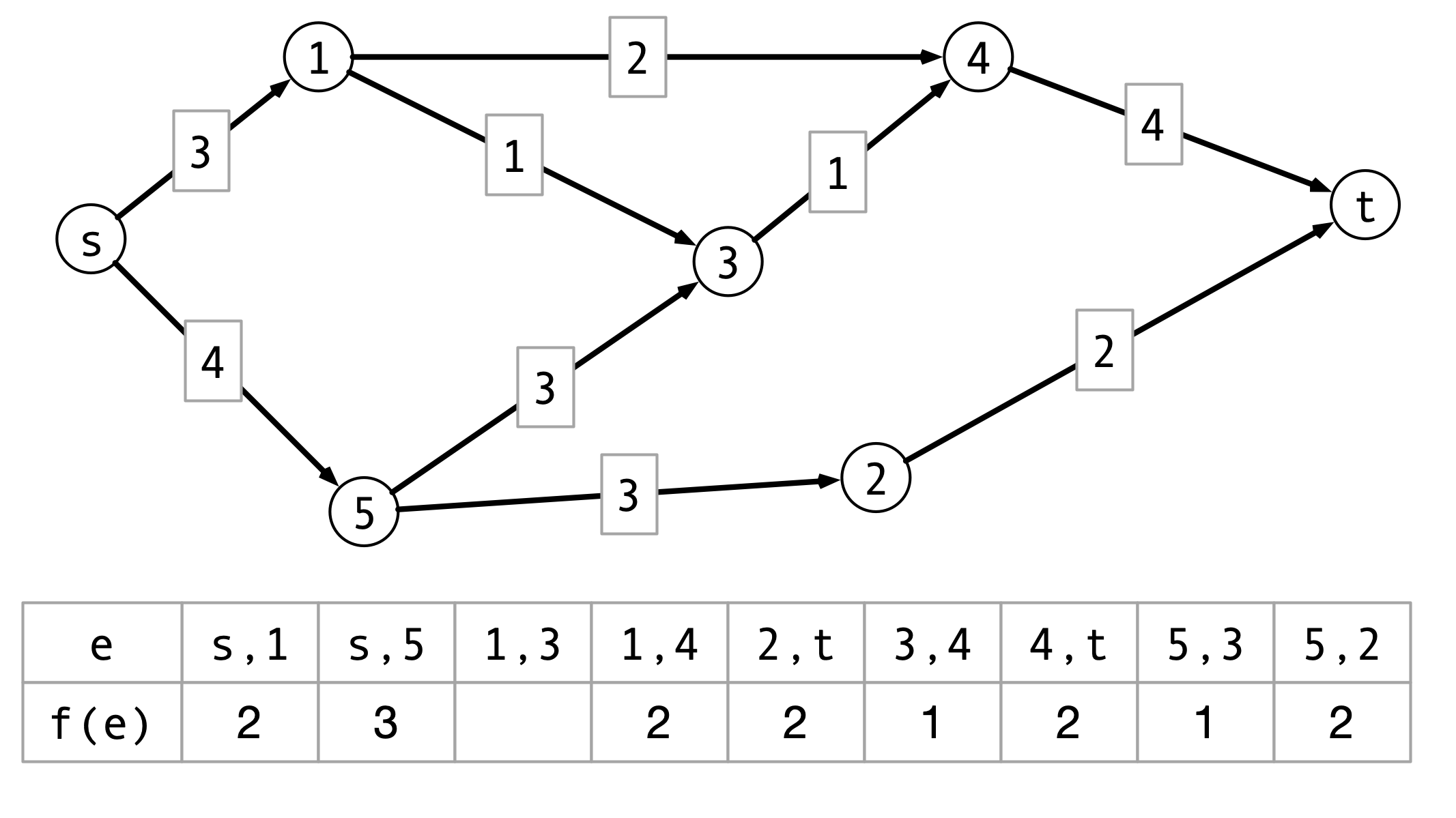
Ford-Fulkerson Example

Questions

How do we…

1. find augmenting path $P$ from $s$ to $t$?

2. update flow $f$ according to $P$?

3. update residual graph $G_f$?

Formalizing Ford-Fulkerson

  MaxFlow(G, s, t):
    Gf <- G
    f <- zero flow
    P <- FindPath(Gf, s, t)
    while P is not null do:
      b <- min capacity of any edge in P
      Augment(Gf, f, P, b)
      P <- FindPath(Gf, s, t)
    endwhile
    return f

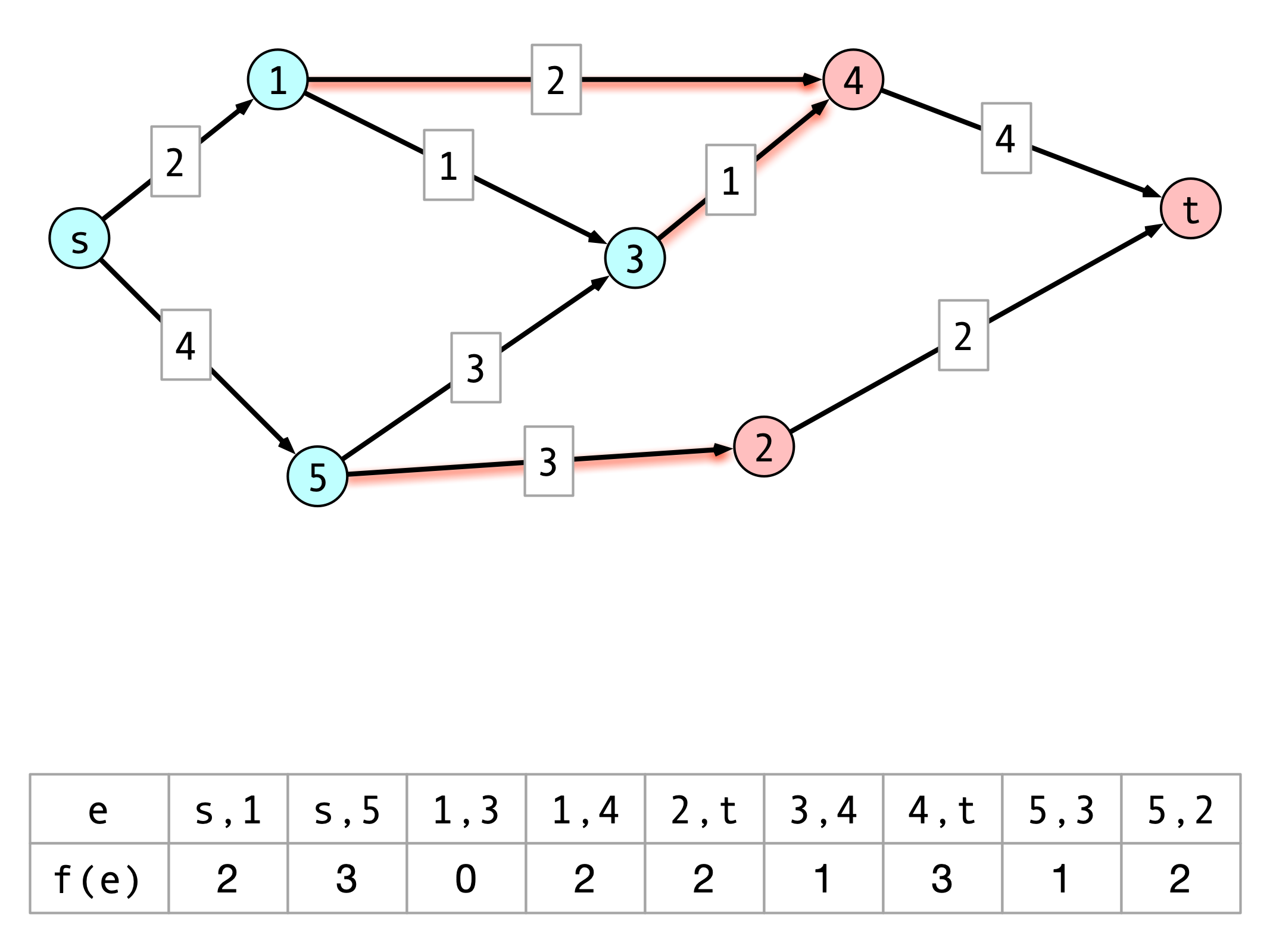
Augment Procedure

  Augment(Gf, f, P, b):
    for each edge (u, v) in P
      if (u, v) is forward edge then
        f(u, v) <- f(u, v) + b
        c(u, v) <- c(u, v) - b
        c(v, u) <- c(v, u) + b
      else
        f(v, u) <- f(v, u) - b
        c(v, u) <- c(v, u) + b
        c(u, v) <- c(u, v) - b

Running Time

Assume:

1. all capacities are integers
2. $C = $ sum of capacites of edges out of $s$

Observe:

1. How long to find augmenting path $P$?

2. How long to run Augment?

3. How many iteraions of find/augment?

Conclude: Overall running time?

Optimality of Flow?

Question. How do we know this flow is optimal?

Cuts

Definition. An $s$ - $t$ cut $(A, B)$ is a partition of vertices into two disjoint sets with $s$ in $A$ and $t$ in $B$.

The capacity of $(A, B)$, denoted $\capacity(A, B)$ is the sum of the capacities of the edges out of $A$.

Cut Example

Correctness of Ford-Fulkerson

Idea. Relate values of flows to capacities of cuts:

• max flow = min cut

Outline:

• for any cut $(A, B)$, net flow across cut = value of flow
  • $\implies$ max flow $\leq$ min cut
• if $f$ has no augmenting path in residual graph, then there is a cut with net flow = value of cut
  • $\implies$ value of $f$ = capacity of cut
  • $\implies \val(f) = \capacity(A, B) \geq $ min cut

Together these imply Ford-Fulkerson produces max flow

Max Flow/Min Cut Example

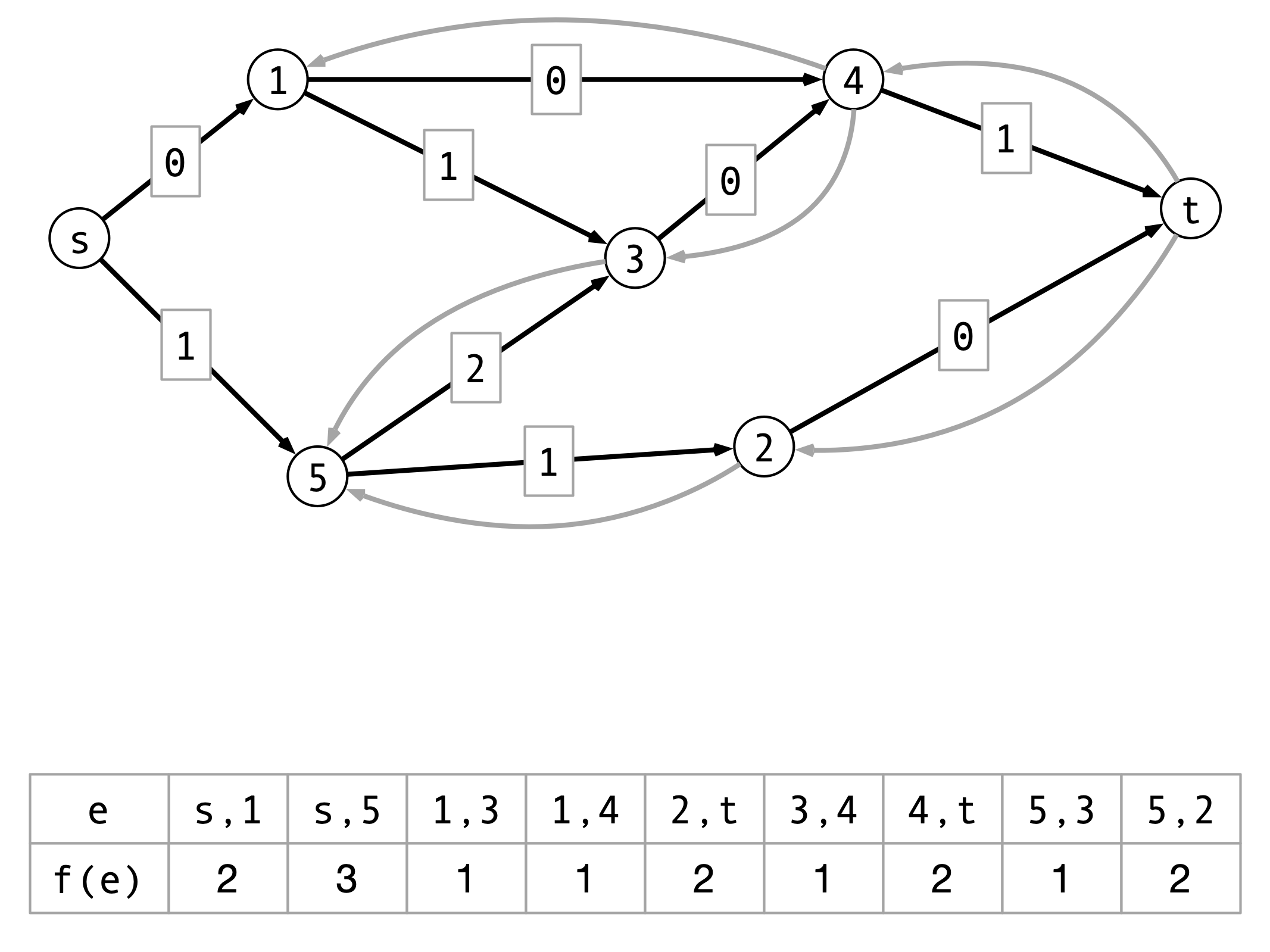
Claim 1

For any $s$ - $t$ cut $(A, B)$ and flow $f$, $\val(f) = f^{\text{out}}(A) - f^{\text{in}}(A)$

• $f^{\text{out}}(A) = $ flow out of $A$
• $f^{\text{in}}(A) = $ flow into $A$

Consequence. For all cuts $(A, B)$, $\val(f) \leq \capacity(A, B)$

Claim 1 Illustration

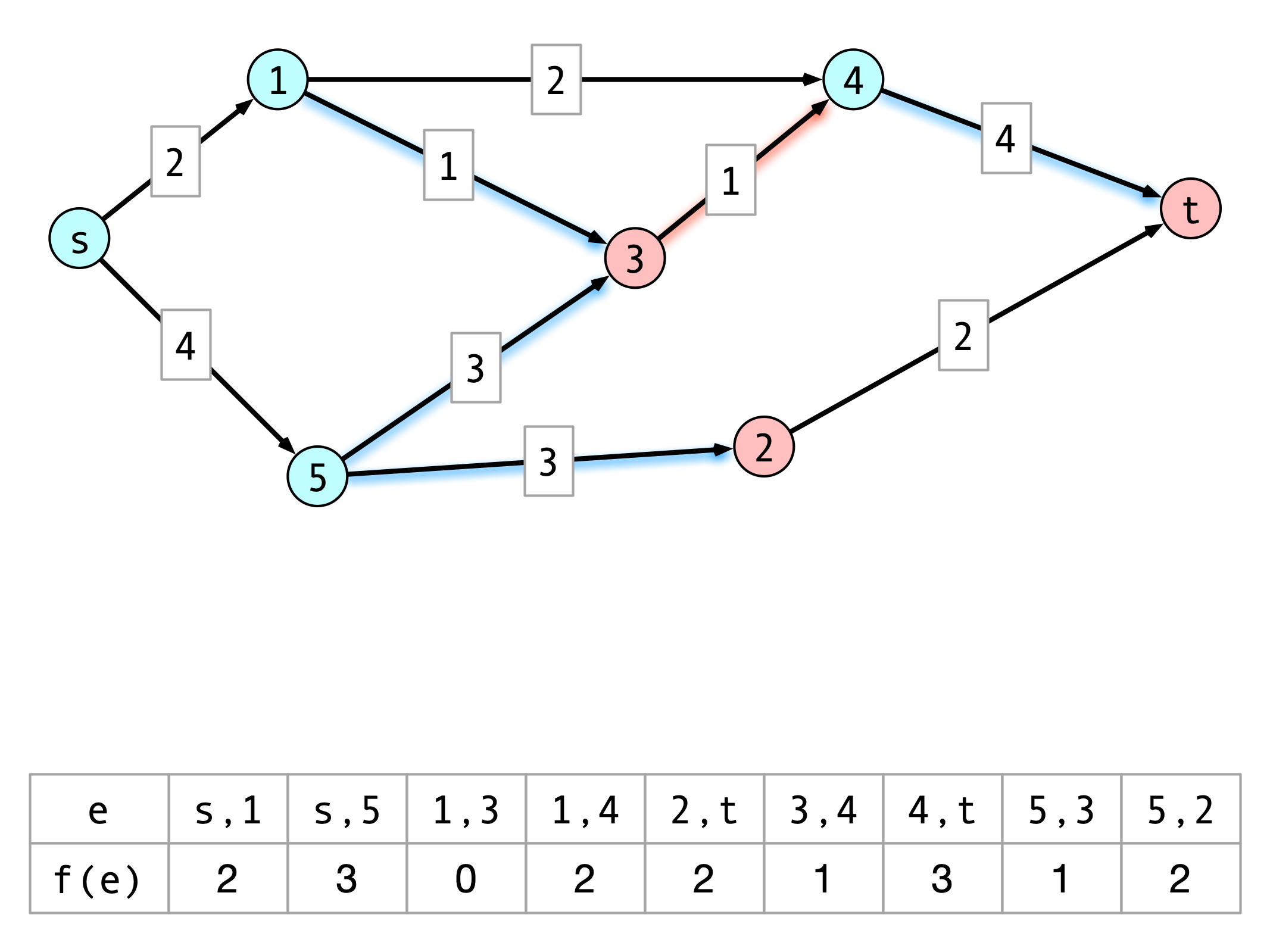
Claim 2

Suppose $f$ does not have an augmenting path in the auxiliary graph.

• $A^* = $ nodes reachable from $s$ in auxiliary graph
• $B^* = $ nodes not reachable

Then $\val(f) = \capacity(A^*, B^\star)$

Claim 2 Illustration

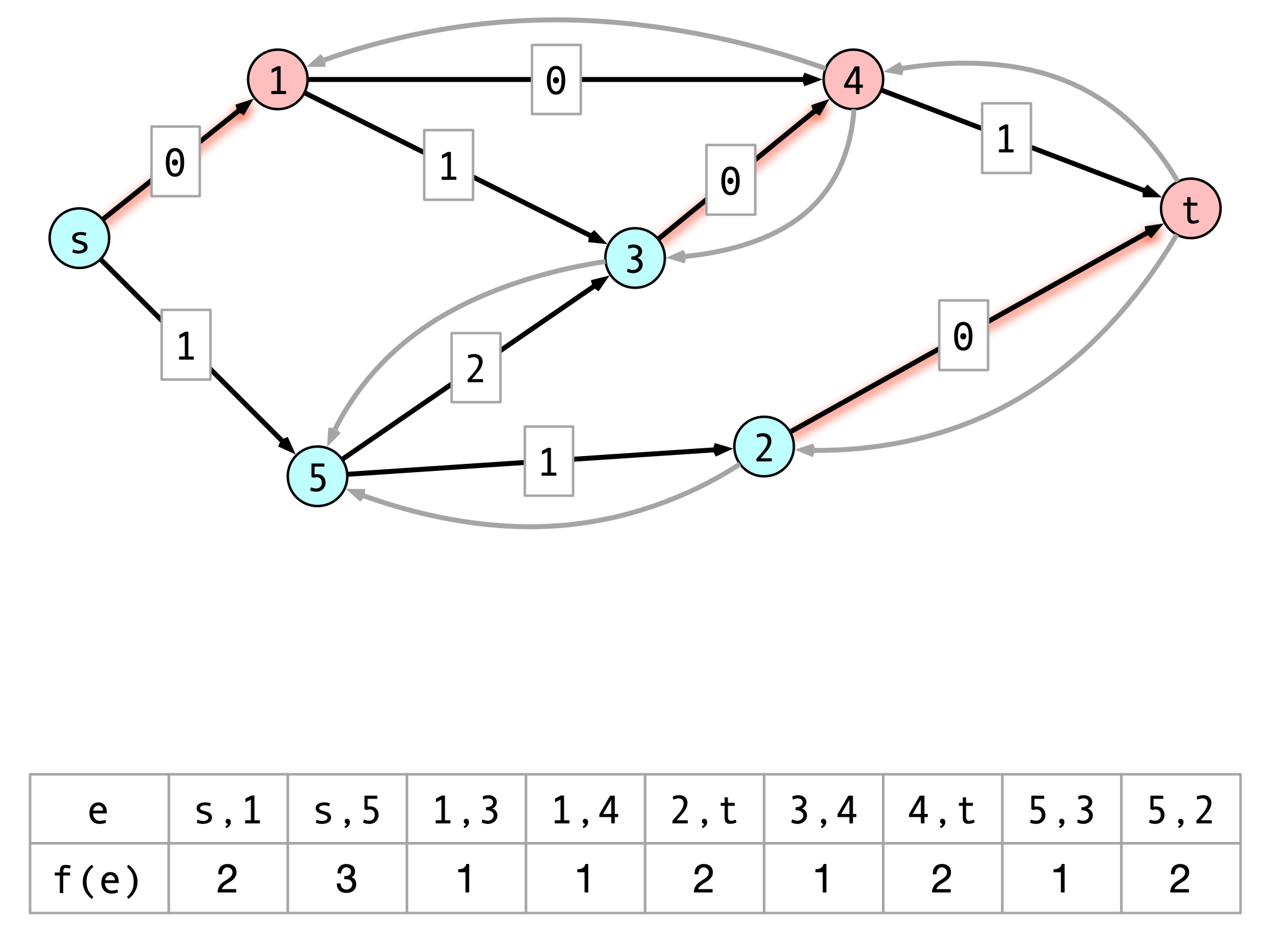
Correctness Follows

Consider flow $f$ found by Ford-Fulkerson.

1. By claim 1, no flow can have value larger than any cut capacity
2. By claim 2, $\val(f) = \capacity(A, B)$

These imply:

1. $f$ is a maximum flow
2. $(A, B)$ is a minimum cut

Conclusion

$G = (V, E)$ a weighted, directed graph with minimum cut capacity $C$.

Ford-Fulkerson finds maximum flow in time $O(C m)$.

• can be modified to find minimum cut as well

Next Time

1. Midterm on Wednesday
2. Stable Matching + Will’s research on Friday
3. Reductions and NP completeness after break