Lecture 29: Network Flow II

$ \def\opt{ {\mathrm{opt}} } \def\val{ {\mathrm{val}} } $

COSC 311 Algorithms, Fall 2022

Last Time

Network Flow

A new interpretation of directed graphs:

• network of (directional) pipes
• weights are capacities
  • how much fluid can flow through piper per time
• designated source node $s$
  • all edges directed away from $s$
• designated sink or destination node $t$
  • all edges directed towards $t$

Question. How much fluid be routed from $s$ to $t$ per unit time?

Flows, Formally

Setup.

• $G = (V, E)$ a directed graph, $s, t$ source and sink
• $c(u,v)$ is capacity of edge $(u, v)$

Flows. An s-t flow $f$ is a function $f : E \to \mathbf{R}^+$ satisfying:

1. capacity constraints: for each edge $e$, $f(e) \leq c(e)$
2. conservation: for every vertex $v \neq s, t$, flow into $v = $ flow out of $v$:
   • $\sum_{x \to v} f(x, v) = \sum_{v \to y} f(v, y)$

The value of the flow $f$ is $\val(f) = \sum_{s \to v} f(s, v)$

Flow Example

Max Flow Problem

Input.

• weighted directed graph $G = (V, E)$
  • weights = edge capacities $> 0$
• source $s$, sink $t$
  • all edges oriented out of $s$
  • all edges oriented into $t$

Output.

• flow $f$ of maximum value
  • $\val(f) = \sum_{s \to v} f(s, v)$

A Simple Greedy Strategy

Repeat until done:

1. find an “unsaturated” path $P$ from $s$ to $t$
2. find minimum (remaining) capacity $b$ along $P$
3. route $b$ units of flow along $P$

Greedy Approach Example

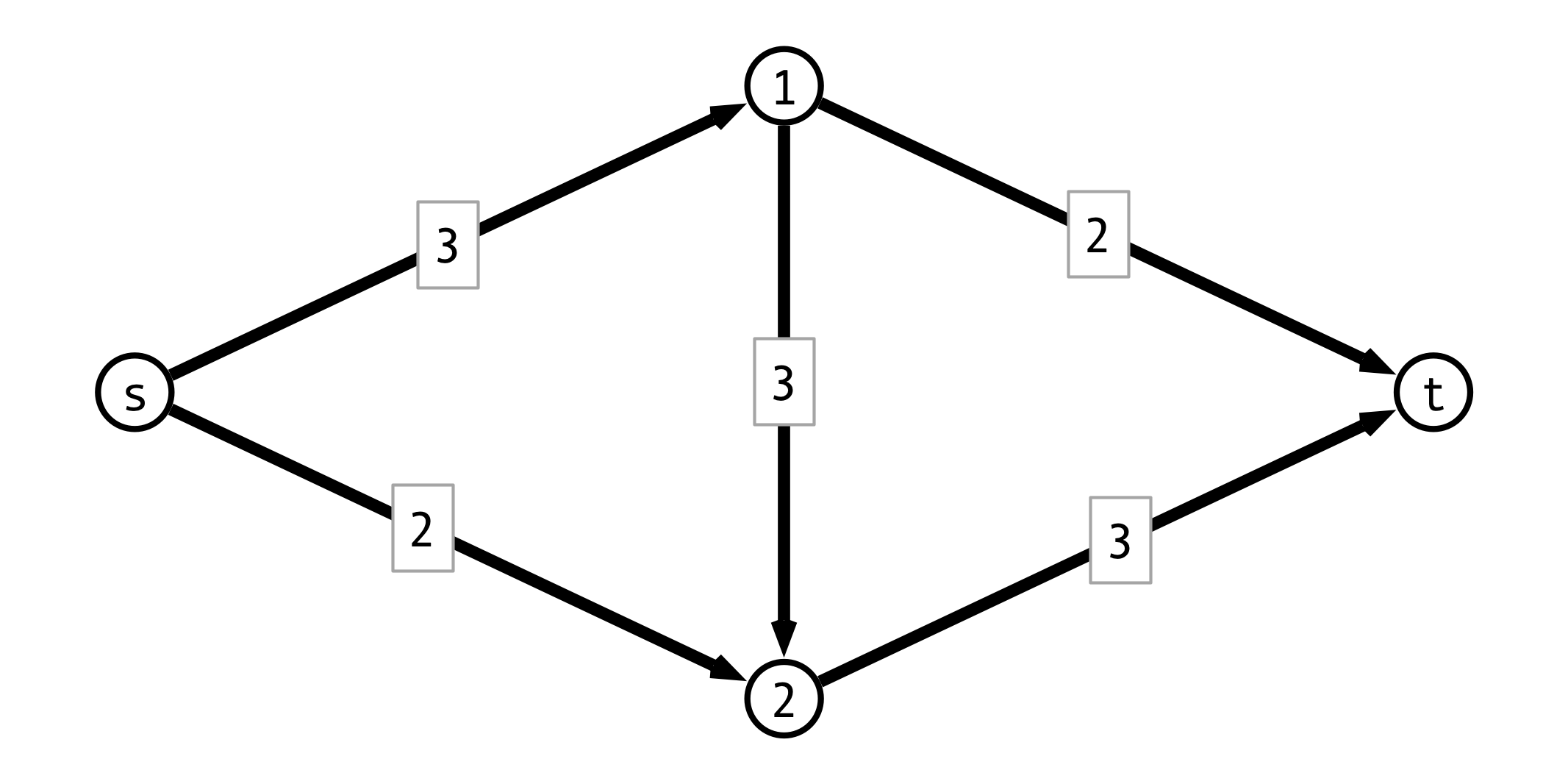
Choosing Different First Path

Greedy Issue

Flow along $P$ may block other viable paths

Question. How to fix this?

Augmenting Paths

Idea. Add “undo” feature for each edge

• if $f$ routes $f(u, v) \leq c(u, v)$ flow from $u$ to $v$, add reverse edge $(v, u)$ with capacity $c(v, u) = f(u, v)$

• using $(v, u)$ corresponds to “pushing back” flow from $(u, v)$

• if an alternate route for this flow can be found, then more flow can be routed through $u$

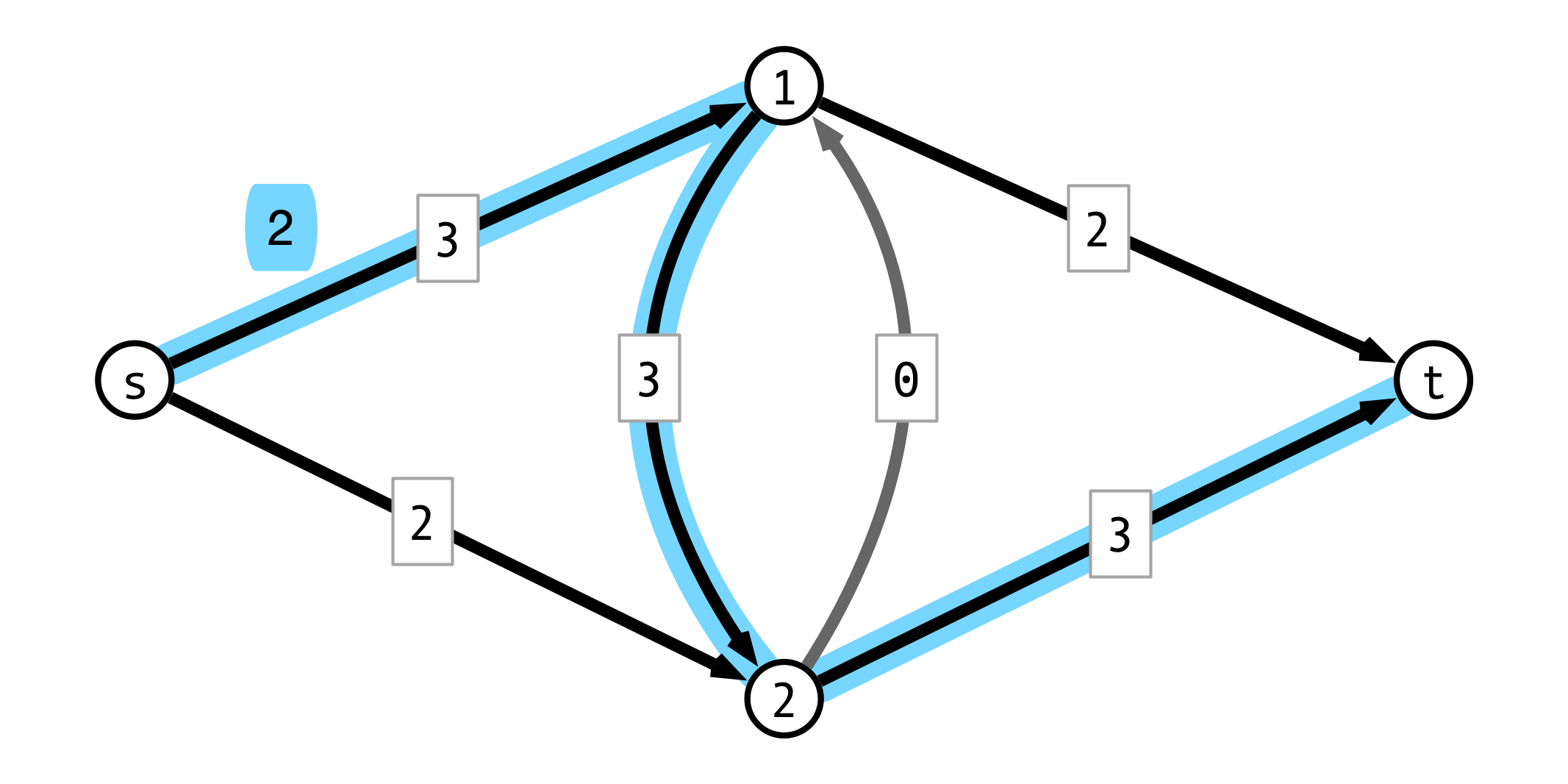
Pushing Back Example

The Residual Graph

• $G = (V, E)$ original graph
• $f$ a flow on $G$

Residual graph $G_f = (V_f, E_f)$

• vertex set $V_f = V$
• for each $(u, v) \in E$, add $(v, u)$ to $E_f$
  • $(u, v)$ is forward edge
  • $(v, u)$ is backward edge
• in $G_f$ capacity of $(u, v)$ is:
  • $c(u, v) - f(u, v)$ if $(u, v) \in E$ (forward edge)
  • $f(v, u)$ if $(v, u) \in E$ (backward edge)

Residual Graph Example

Ford-Fulkerson Algorithm

Very high level

1. Initialize residual graph, flow $f$
2. While there is a path from $s$ to $t$ in residual graph do:
   • find path $P$ from $s$ to $t$
     • ignore edges with capacity $0$
   • $b \leftarrow$ minimum capacity along $P$
   • augment flow $f$ by $b$ along $P$
   • update residual graph
3. return $f$

Questions

How do we…

1. find a path $P$ from $s$ to $t$?

2. update flow $f$?

3. update residual graph $G_f$?

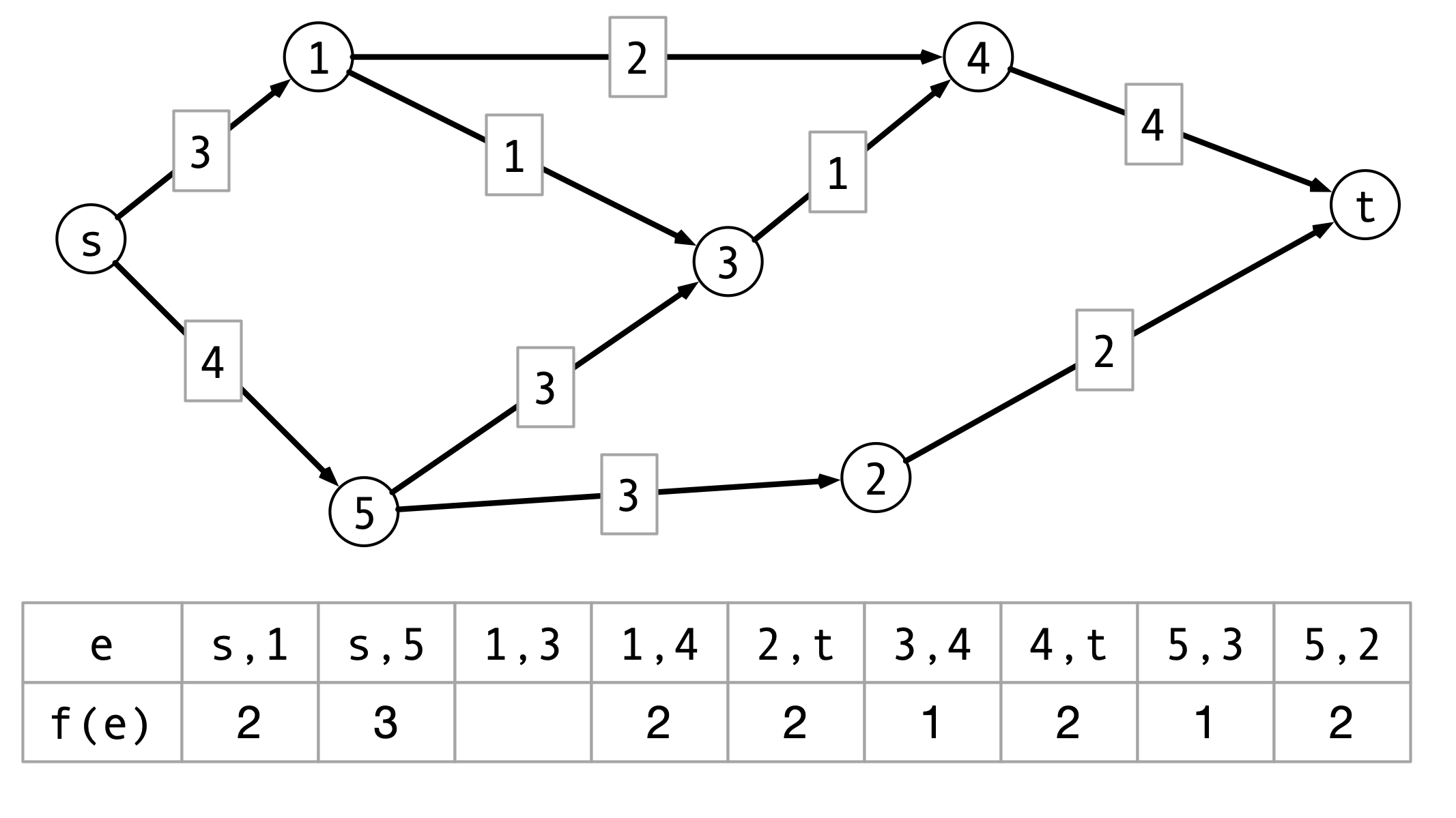
Example

Formalizing Ford-Fulkerson

  MaxFlow(G, s, t):
    Gf <- G
    f <- zero flow
    P <- FindPath(Gf, s, t)
    while P is not null do:
      b <- min capacity of any edge in P
      Augment(Gf, f, P, b)
      P <- FindPath(Gf, s, t)
    endwhile
    return f

Augment Procedure

  Augment(Gf, f, P, b):
    for each edge (u, v) in P
      if (u, v) is forward edge then
        f(u, v) <- f(u, v) + b
        c(u, v) <- c(u, v) - b
        c(v, u) <- c(v, u) + b
      else
        f(v, u) <- f(v, u) - b
        c(v, u) <- c(v, u) + b
        c(u, v) <- c(u, v) - b

Running Time

Assume:

1. all capacities are integers
2. $C = $ sum of capacites of edges out of $s$

Observe:

1. How long to find augmenting path $P$?

2. How long to run Augment?

3. How many iteraions of find/augment?

Conclude: Overall running time?

Optimality of Flow?

Question. How do we know this flow is optimal?

Next Time

Ford-Fulkerson Correctness:

• Maximum Flow = Minimum Cut