Lecture 28: Network Flow

$ \def\opt{ {\mathrm{opt}} } \def\val{ {\mathrm{val}} } $

COSC 311 Algorithms, Fall 2022

Last Time

Bellman-Ford Algorithm for SSSP

Definition. For each $j = 0, 1, \ldots, n-1$ define $d_j(u, v) = $ length of shortest path from $u$ to $v$ consisting of $\leq j$ hops.

Bellman-Ford Algorithm

  Bellman-Ford(V, E, w, u)
    d <- 2d array [0..n-1, 1..n]
    for v = 1 to n do d[0, v] <- infinity
    d[0, u] <- 0
    for j = 1 to n-1 do
      for each vertex v in V set d[j, v] <- d[j-1,v]
      for each vertex v in V
        for each neighbor x of v
          d[j, x] <- Min(d[j, x], d[j-1, v] + w[v, x])
    return d[n-1]

Running time is $O(m n)$ if $G$ has $n$ vertices and $m$ edges.

Correctness

Claim. For all $j = 0, 1, \ldots, n-1$ and for all vertices $v$, $d[j, v]$ stores length of shortest path from $u$ to $v$ with $j$ or fewer hops. I.e., $d[j, v] = d_j(v)$

Proof. Induction on $j$.

Base case, $j = 0$.

Inductive Step, $j-1 \implies j$

• suppose $d[j-1, v] = d_{j-1}(v)$ for all $v$
• consider shortest path $P$ of $\leq j$ hops from $u$ to $v$
• let $x$ be penultimate vertex in $P$
• then $d_j(v) = d_{j-1}(x) + w(x, v)$
• by inductive hypothesis, $d_{j-1}(x) = d[j-1,x]$
• therefore in iteration $j$, get $d[j, v] \leq d[j-1,x] + w(x, v) = d_{j-1}(x) + w(x, v) = d_j(v)$
• also have $d[j, v] \geq d_j(v)$ (why?)
• so $d[j, v] = d_j(v)$

Conclusion

If $G$ has no negative weight cycles, then Bellman-Ford solves single source shortest paths in $O(m n)$ time.

Dijkstra vs Bellman-Ford?

Running times:

• Dijkstra: $O(m \log n)$
• Bellman-Ford: $O(m n)$

Why pick Bellman-Ford over Dijkstra?

Bellman-Ford Again

  Bellman-Ford(V, E, w, u)
    d <- 2d array [0..n-1, 1..n]
    for v = 1 to n do d[0, v] <- infinity
    d[0, u] <- 0
    for j = 1 to n-1 do
      for each vertex v in V set d[j, v] <- d[j-1,v]
      for each vertex v in V
        for each neighbor x of v
          d[j, x] <- Min(d[j, x], d[j-1, v] + w[v, x])
    return d[n-1]

Cold War

Soviet Rail Network, ca. 1955

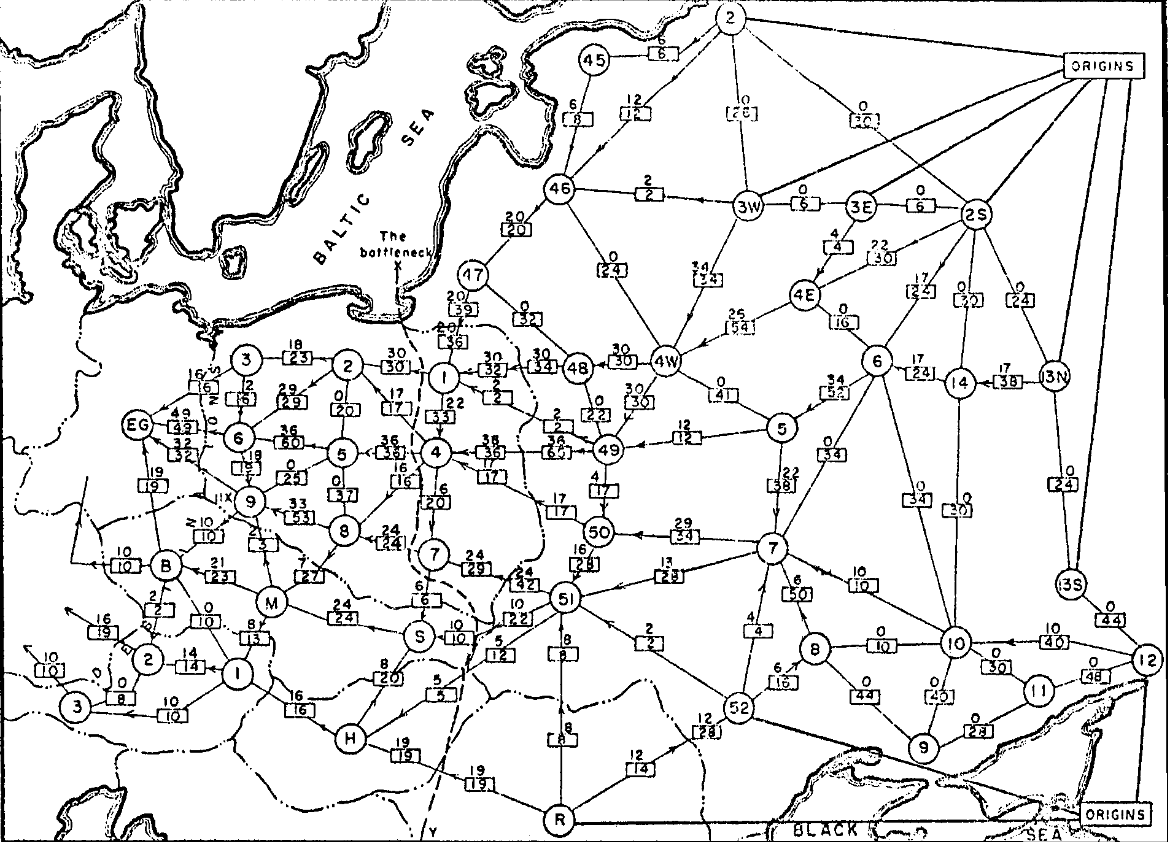
Networks to Graphs

Modeling the network:

• nodes represent railway junctions
• edges represent rail lines
• weights represent capacities of lines
  • capacity $=$ tonnage that can cross line per unit time
  • proportional to cost of disrupting line

Network Flow

A new interpretation of directed graphs:

• network of (directional) pipes
• weights are capacities
  • how much fluid can flow through piper per time
• designated source node $s$
  • all edges directed away from $s$
• designated sink or destination node $t$
  • all edges directed towards $t$

Question. How much fluid be routed from $s$ to $t$ per unit time?

Example

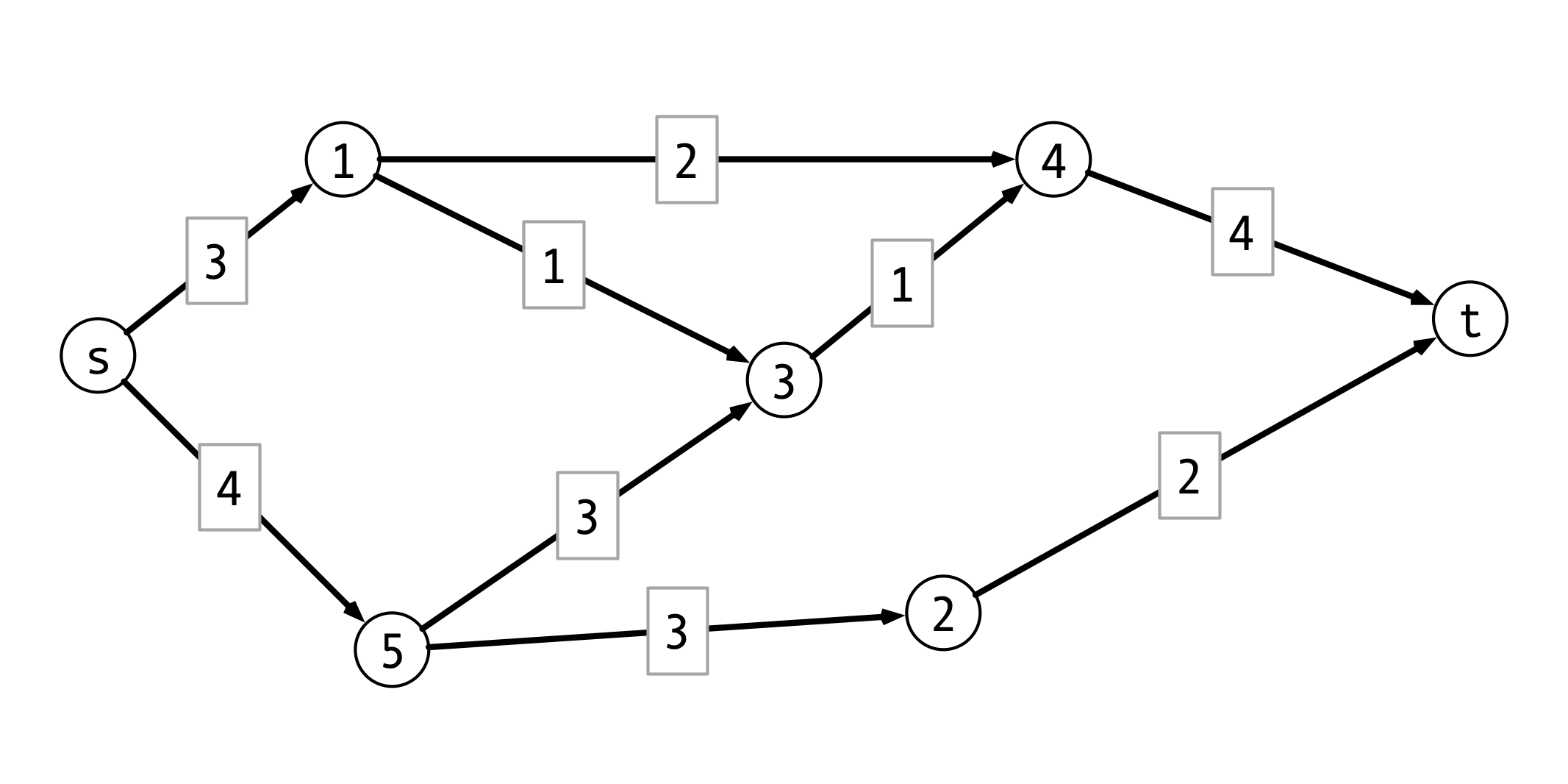
Flows, Formally

Setup.

• $G = (V, E)$ a directed graph, $s, t$ source and sink
• $c(u,v)$ is capacity of edge $(u, v)$

Flows. An s-t flow $f$ is a function $f : E \to \mathbf{R}^+$ satisfying:

1. capacity constraints: for each edge $e$, $f(e) \leq c(e)$
2. conservation: for every vertex $v \neq s, t$, flow into $v = $ flow out of $v$:
   • $\sum_{x \to v} f(x, v) = \sum_{v \to y} f(v, y)$

The value of the flow $f$ is $\val(f) = \sum_{s \to v} f(s, v)$

Flow Example 1

Flow Example 2

Max Flow Problem

Input.

• weighted directed graph $G = (V, E)$
  • weights = edge capacities $> 0$
• source $s$, sink $t$
  • all edges oriented out of $s$
  • all edges oriented into $t$

Output.

• flow $f$ of maximum value
  • $\val(f) = \sum_{s \to v} f(s, v)$

A Simple Greedy Strategy

Repeat until done:

1. find an “unsaturated” path $P$ from $s$ to $t$
2. find minimum (remaining) capacity $b$ along $P$
3. route $b$ units of flow along $P$

Greedy Approach Example

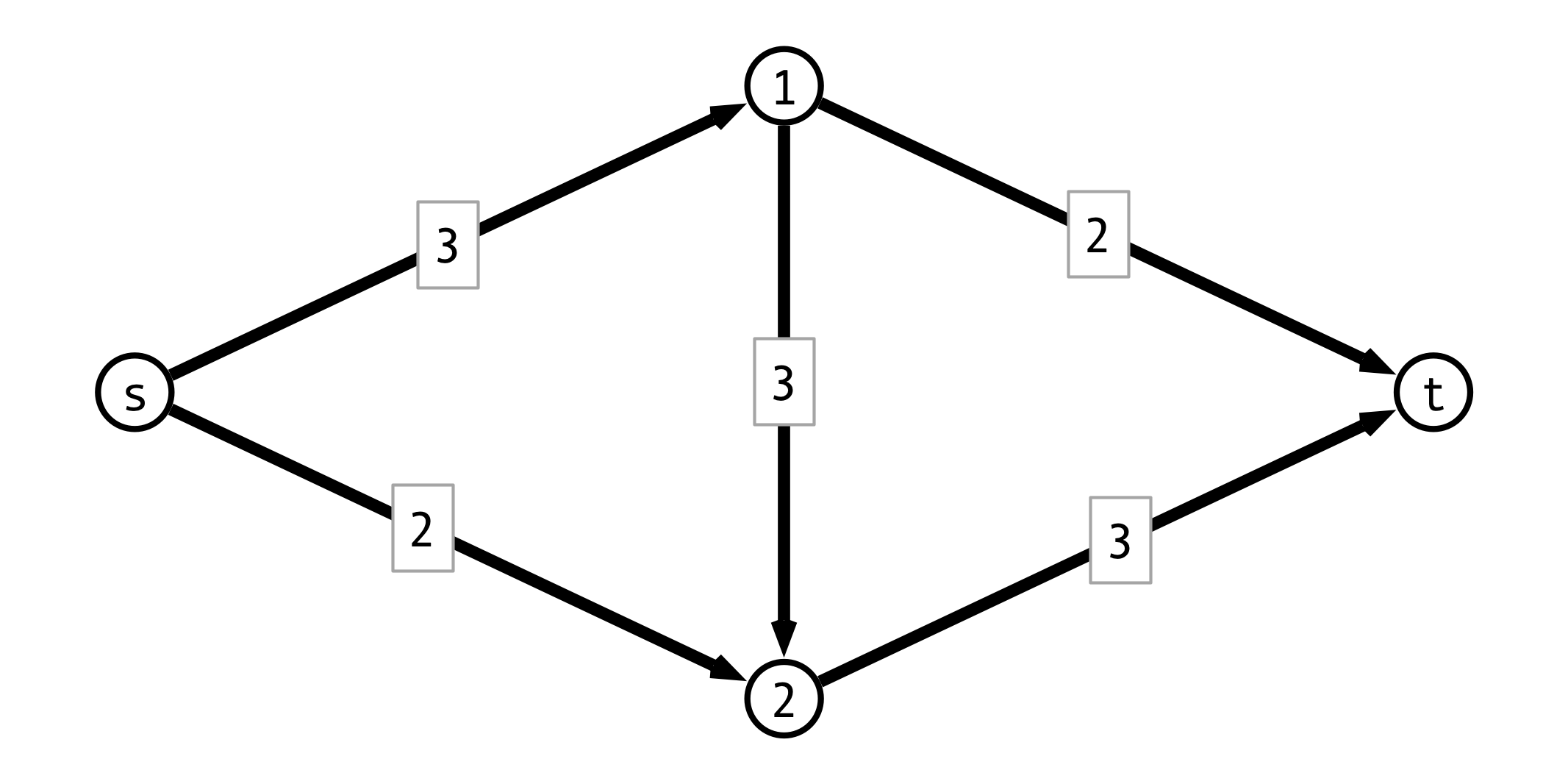
Choosing Different First Path

Greedy Issue

Flow along $P$ may block other viable paths

Question. How to fix this?

Augmenting Paths

Idea. Add “undo” feature for each edge

• if $f$ routes $f(u, v) \leq c(u, v)$ flow from $u$ to $v$, add reverse edge $(v, u)$ with capacity $c(v, u) = f(u, v)$

• using $(v, u)$ corresponds to “pushing back” flow from $(u, v)$

• if an alternate route for this flow can be found, then more flow can be routed through $u$

Pushing Back Example

The Residual Graph

• $G = (V, E)$ original graph
• $f$ a flow on $G$

Residual graph $G_f = (V_f, E_f)$

• vertex set $V_f = V$
• for each $(u, v) \in E$, add $(v, u)$ to $E_f$
  • $(u, v)$ is forward edge
  • $(v, u)$ is backward edge
• in $G_f$ capacity of $(u, v)$ is:
  • $c(u, v) - f(u, v)$ if $(u, v) \in E$ (forward edge)
  • $f(v, u)$ if $(v, u) \in E$ (backward edge)

Residual Graph Example

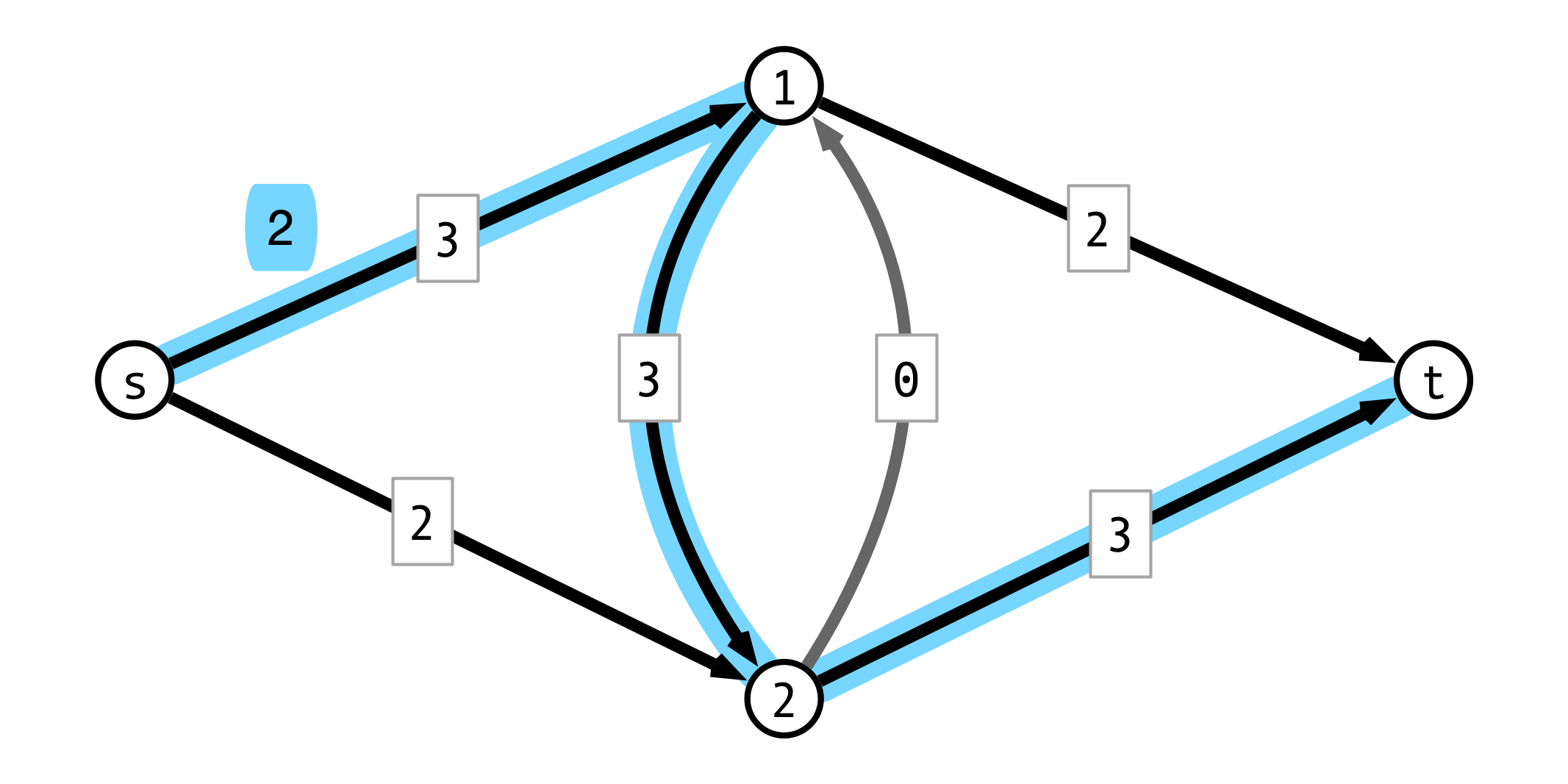
Ford-Fulkerson Algorithm

Very high level

1. Initialize residual graph, flow $f$
2. While there is a path from $s$ to $t$ in residual graph do:
   • find path $P$ from $s$ to $t$
     • ignore edges with capacity $0$
   • $b \leftarrow$ minimum capacity along $P$
   • augment flow $f$ by $b$ along $P$
   • update residual graph
3. return $f$

Question

We’ve found a path $P$ with minimum capacity $b > 0$!

Question. How do we…

1. update flow $f$?
2. update residual graph $G_f$?

Example

Formalizing Ford-Fulkerson

  MaxFlow(G, s, t):
    Gf <- G
    f <- zero flow
    P <- FindPath(Gf, s, t)
    while P is not null do:
      b <- min capacity of any edge in P
      Augment(Gf, f, P, b)
      P <- FindPath(Gf, s, t)
    endwhile
    return f

Augment Procedure

  Augment(Gf, f, P, b):
    for each edge (u, v) in P
      if (u, v) is forward edge then
        f(u, v) <- f(u, v) + b
        c(u, v) <- c(u, v) - b
        c(v, u) <- c(v, u) + b
      else
        f(v, u) <- f(v, u) - b
        c(v, u) <- c(v, u) + b
        c(u, v) <- c(u, v) - b

Running Time

Assume:

1. all capacities are integers
2. $C = $ sum of capacites of edges out of $s$

Observe:

1. How long to find augmenting path $P$?

2. How long to run Augment?

3. How many iteraions of find/augment?

Conclude: Overall running time?

Next Time

Ford-Fulkerson Correctness!