Lecture 26: Sequence Alignment and Shortest Paths
$ \def\opt{ {\mathrm{opt}} } $
COSC 311 Algorithms, Fall 2022
Overview
- Sequence Alignment
- Shortest Paths, Revisited
Matching Between Strings
Given strings $X$ and $Y$ form a matching between characters
- matching $M$ is a set of pairs of matched indices
Rules for matching:
- each character is matched with at most one other character
- some characters may be unmatched
- matched characters cannot “cross”
- if $(i, j)$, $(i’, j’)$ are matched with $i < i’$, then $j < j’$
Sequence Alignment Problem
Input:
- Sequences $X$ and $Y$ of characters of length $n$ and $m$, respectively
- Penalties $\delta, \alpha$ for omission/mismatch
Output:
- A matching $M$ between indices of $X$ and $Y$
- $M$ minimizes total penalty of matching
An Observation
Suppose
- $X$ sequence of length $n$
- $Y$ sequence of length $m$
- $M$ a matching between $[1, n]$ and $[1, m]$
Claim. Then at least one of the following holds:
- $(n, m)$ is in $M$
- $n$ is unmatched in $M$
- $m$ is unmatched in $M$
Why?
A Recursive Solution?
Idea. Use previous claim to give recursive characterization of optimal alignment.
How?
Define
- $\opt(i, j) = $ minimum penalty of aligning $X[1..i]$ and $Y[1..j]$
- $M_{i,j}$ is minimum penalty matching between $X[1..i]$ and $Y[1..j]$
- by claim, there are three cases
- $(i, j) \in M_{i, j}$
- $i$ unmatched in $M_{i, j}$
- $j$ unmatched in $M_{i, j}$
Recursive Solution?
Question. What is a recurrence relation for $\opt(i, j)$?
Iterative Solution
Construct a two dimensional array p[0..n, 0..m]
-
p[i, j]should store $\opt(i, j)$
Question 1. How to initialize p?
Question 2. How to fill out p?
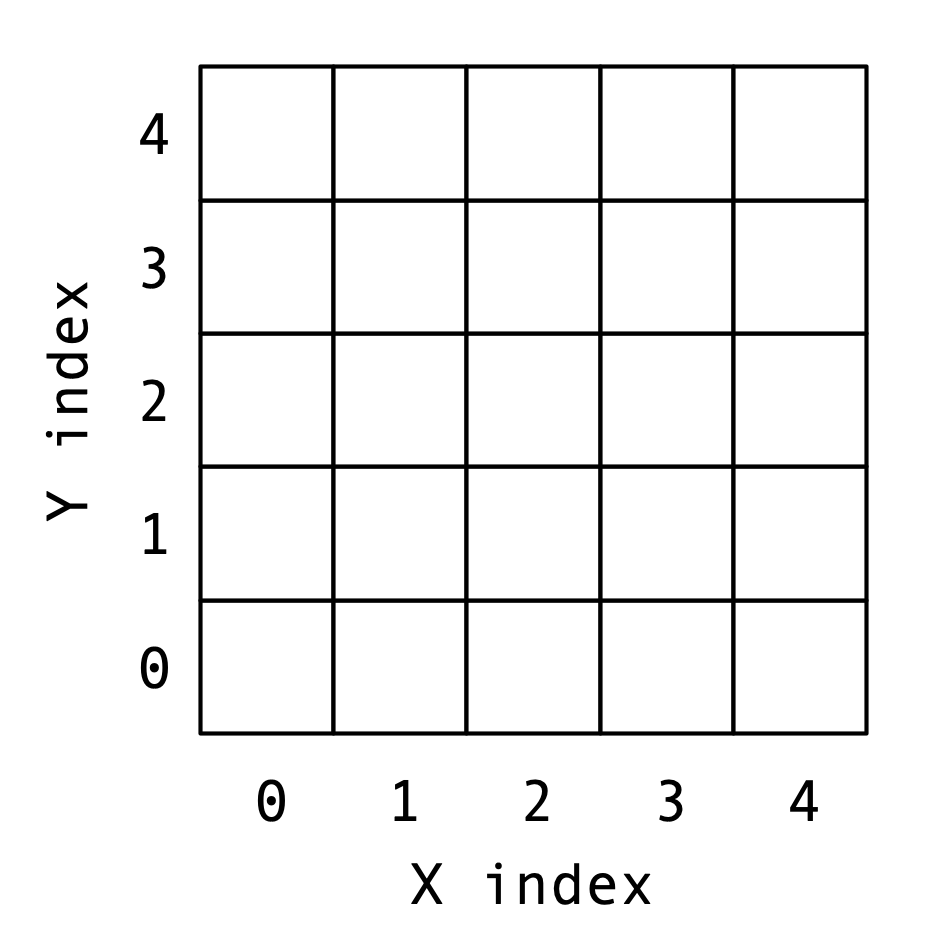
Example
- $X = [R, I, T, E]$
- $Y = [T, I, E, R]$
- $\delta = \alpha = 1$
Algorithm Pseudocode
Alignment(X, Y, a, d):
p <- 2d array of dimension (n+1) x (m+1)
for i from 0 to n, p[i, 0] <- i * d
for j from 0 to m, p[0, j] <- j * d
for i from 1 to n
for j from 1 to m
unmatchX <- p[i-1, j] + d
unmatchY <- p[i,j-1] + d
match <- p[i-1,j-1]
if X[i] != Y[j] then match <- match + a
p[i, j] <- Min(unmatchX, unmatchY, match)
return p[n, m]
Running time?
Conclusion
Optimal alignment between strings can be found in $O(n m)$ time where strings have lengths $n$ and $m$, respectively.
Shortest Paths, Revisited
Directed Graphs and Paths
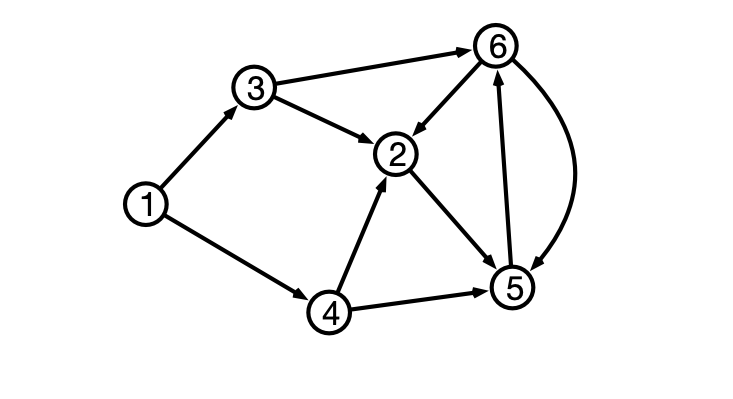
Representing Directed Graphs
Adjacency List
- $v$’s neighbors are outgoing neighbors

Previously
Single Source Shortest Paths (SSSP):
Input:
- (Directed) graph $G = (V, E)$, edge weights $w$
- Starting vertex $u$
Output:
- $d(v) = $ distance from $u$ to $v$ for every vertex $v$
Previous Algorithms
- Breadth-first Search (BFS)
- solves SSSP when all edge weights are $1$
- Dijkstra’s Algorithm
- solves SSSP when all edge weights are $\geq 0$
Question. What if edge weights can be negative?
Negative Dijkstra
Assumption
Assume. $G$ does not contain any negative weight cycles.
Why?
Observation
Claim. $G$ a graph with $n$ vertices, $u, v$ vertices in $G$. If $G$ does not contain negative weight cycles, then the shortest (weighted) path from $u$ to $v$ contains at most $n-1$ edges.
Why?
Intuition
Suppose shortest path from $u$ to $x$ contains $j$ hops.
- $v$ is $x$’s “parent” along path
- $d(u, x) = d(u, v) + w(v, x)$
- shortest path from $u$ to $v$ has $j-1$ hops
Dynamic Programming Approach
Idea. For each vertex $v$ and each $j = 1, 2, \ldots, n-1$ compute $d_j(u, v) = $ length of shortest path from $u$ to $v$ with at most $j$ hops.
- Note $d(u, v) = d_{n-1}(u, v)$.
Questions
Question 1. How to initialize $d_0(u, v)$?
Question 2. Given $d_j(u, v)$ for all v, how to find $d_{j+1}(u, v)$?
Illustration
Bellman-Ford Algorithm
Bellman-Ford(V, E, w, u)
d <- 2d array [0..n-1, 1..n]
for v = 1 to n do d[0, v] <- infinity
d[0, u] <- 0
for j = 1 to n-1 do
for each vertex v in V set d[j, v] <- d[j-1,v]
for each vertex v in V
for each neighbor x of v
d[j, x] <- Min(d[j, x], d[j-1, v] + w[v, x])
return d[n-1]
Running time?
Dijkstra vs Bellman-Ford?
Next Time
Network Flow!