Lecture 22: Intro to Dynamic Programming

COSC 311 Algorithms, Fall 2022

Announcements

1. ‘22E Honors Thesis talks Today!

• 4-5pm in SCCE A131

1. Courses Next Semester

   • 225 Algorithms and Visualization
   • 273 Parallel and Distributed Computing

Overview

1. Memoization
2. Profit Maximization, Revisited

So Far

Algorithmic Paradigms

1. Divide and Conquer

2. Greedy

And now…

Dynamic Programming

Features of Dynamic Programming

1. Break problem into smaller sub-problems
2. Iterate over sub-problems to produce solution

Compare to divide and conquer:

1. Break problem into smaller sub-problems
2. Recursively solve sub-problems
3. Combine solutions

Issues with Recursion

Recall the Fibonacci Sequence:

• $1, 1, 2, 3, 5, 8, 13, 21, 34, 55, \ldots$

  Fib(n):
    if n <= 2 then return 1
    return Fib(n-1) + Fib(n-2)

What is Running Time?

  Fib(n):
    if n <= 2 then return 1
    return Fib(n-1) + Fib(n-2)

Redundant Recursive Calls

Recursive subproblems overlap

Memoization

Recursing without recursion

• store results of recursive calls
• iterate over results rather than making recursive calls
  • compute results “bottom up” rather than “top down”
  • iterate over stored values to compute “next” value

How to do for Fibonacci?

Memoized Fibonacci

  MFib(n):
    a <- array of size n
    a[1] <- 1
    a[2] <- 1
    for each index i from 3 to n do
      a[i] <- a[i-1] + a[i-2]
    endfor
    return a[n]

Running Time?

  MFib(n):
    a <- array of size n
    a[1] <- 1
    a[2] <- 1
    for each index i from 3 to n do
      a[i] <- a[i-1] + a[i-2]
    endfor
    return a[n]

The Moral

With memoization, we converted

• recursive procedure
• many redundant recursive calls
• running time $\Omega(2^{n/2})$

into

• iterative procedure
• running time $O(n)$

Profit Maximization

Recall: Profit Maximization

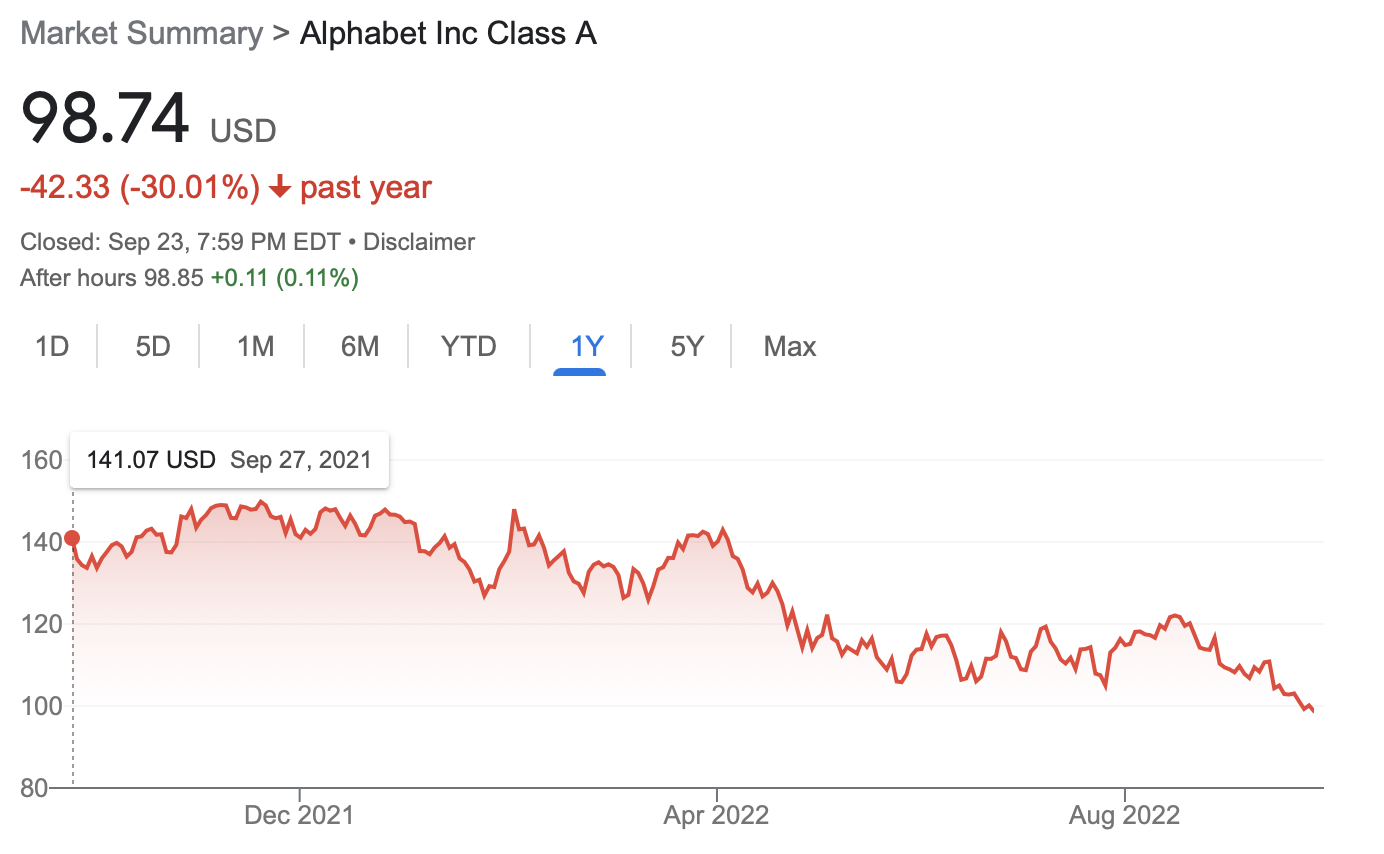
Goal. Pick day $b$ to buy and day $s$ to sell to maximize profit.

Formalizing the Problem

Input. Array $a$ of size $n$

• $a[i] = $ price of Alphabet stock on day $i$

Output. Indices $b$ (buy) and $s$ (sell) with $1 \leq b \leq s \leq n$ that maximize profit

• $p = a[s] - a[b]$

Divide and Conquer Algorithm

  MaxProfit(a, i, j):
    if j - i = 1 then return 0	
    m <- (i + j) / 2	
    left <- MaxProfit(a, i, m)
    right <- MaxProfit(a, m, j)	
    min <- FindMin(a, i, m)
    max <- FindMax(a, m, j)
    return Max(left, right, max - min)

Running time?

Another (Recursive) Procedure?

• consider last day, $n$
• two cases for optimal solution:
  1. max profit achieved by selling on day $n$
  2. max profit achieved by selling before day $n$

Questions.

1. In case 1, how should we determine buy date?

2. In case 2, how should we compute max profit?

Recursive Procedure

  MaxProfit(a, n):
    if n = 1 then return 0
    min <- FindMin(a, n)
    max <- MaxProfit(a, n-1)
    return max(a[n] - min, max)

Running time?

Questions

1. What makes MaxProfit inefficient?

2. What part(s) of the procedure can be memoized?

Memoizing MaxProfit

Create two arrays:

1. min[i] stores minimum value in a[1..i]
2. max[i] stores maximum profit achievable by selling up to time i

Question. How to update these arrays?

Example

Memoized Maximum Profit

  MMaxProfit(a):
    initialize arrays min, max 
    min[1] <- a[1]
    max[1] <- 0
    for i from 2 to n do
      min[i] <- Min(min[i-1], a[i])
      max[i] <- Max(max[i-1], a[i] - min[i])
    endfor
    return max[n]

Correctness

Induction on $n$…

Running Time?

  MMaxProfit(a):
    initialize arrays min, max 
    min[1] <- a[1]
    max[1] <- 0
    for i from 2 to n do
      min[i] <- Min(min[i-1], a[i])
      max[i] <- Max(max[i-1], a[i] - min[i])
    endfor
    return max[n]

Optimization

Can do without arrays for min and max

  MMaxProfit(a):
    min <- a[1]
    max <- 0
    for i from 2 to n do
      min <- Min(min, a[i])
      max <- Max(max, a[i] - min)
    endfor
    return max[n]

Exercise

Update MMaxProfit to return the buy/sell days in addition to the maximum achievable profit.

Next Time

• weighted interval scheduling
• much more!