Lecture 20: Minimum Spanning Trees, Part 3

COSC 311 Algorithms, Fall 2022

$ \def\compare{ {\mathrm{compare}} } \def\swap{ {\mathrm{swap}} } \def\sort{ {\mathrm{sort}} } \def\insert{ {\mathrm{insert}} } \def\true{ {\mathrm{true}} } \def\false{ {\mathrm{false}} } \def\BubbleSort{ {\mathrm{BubbleSort}} } \def\SelectionSort{ {\mathrm{SelectionSort}} } \def\Merge{ {\mathrm{Merge}} } \def\MergeSort{ {\mathrm{MergeSort}} } \def\QuickSort{ {\mathrm{QuickSort}} } \def\Split{ {\mathrm{Split}} } \def\Multiply{ {\mathrm{Multiply}} } \def\Add{ {\mathrm{Add}} } \def\cur{ {\mathrm{cur}} } \def\gets{ {\leftarrow} } $

Announcements

1. Masks still required in class
2. No class on Monday 10/24
3. HW 03, Question 1:
   • $n = 2^B$
   • array contains $0, 1, \ldots, n - 1$ (not in order)
   • values represented as $B$ bit numbers
4. HW 03 now due Sunday

Last Time

Prim’s algorithm for Minimum Spanning Trees:

• Grow a tree from an arbitrary seed vertex
• Each step, add minimum weight edge out of tree

Cut Claim:

• if $T$ an MST, $U, V - U$ a cut, $e$ min weight cut edge
• then $T$ contains $e$

Prim correctness follows from cut claim

MSTs, Another Way

Prim:

• Grow tree greedily from a single seed vertex
• Maintain a (connected) tree

Edge Centric View:

• Maintain a collection of edges (not necessarily a tree)
• Add edges to collection to eventually build an MST

Questions:

• How to prioritize edges?
• How to determine whether or not to include an edge?

Picture

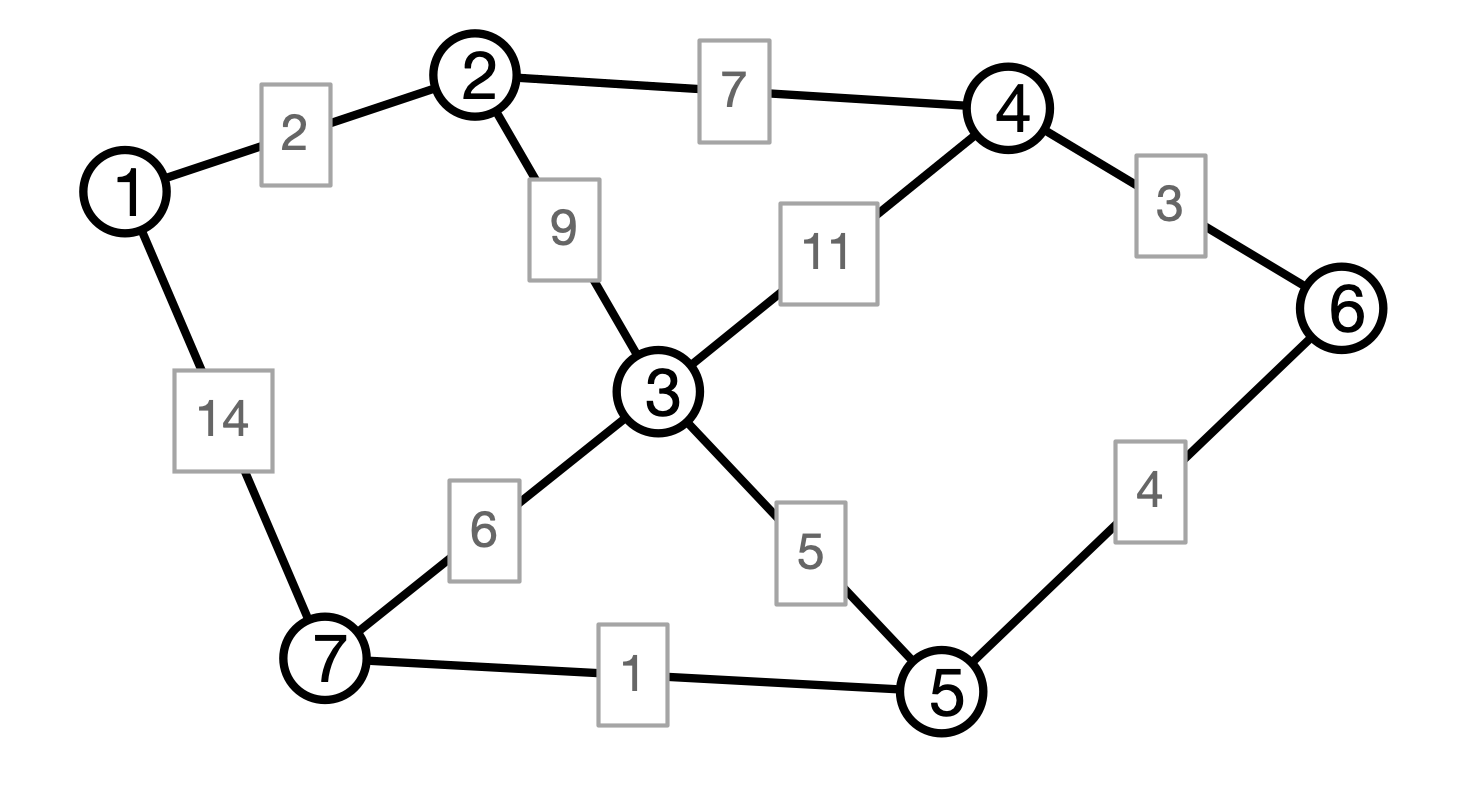
Kruskal’s Algorithm

  Kruskal(V, E, w):
    C <- collection of components
      initially, each vertex is own component
    F <- empty collection
    # iterate in order of increasing weight
    for each edge e = (u, v) in E 
      if u and v are in different components then
        add (u, v) to F
        merge components containing u and v
      endif
    endfor
    return F

Kruskal Illustration

Kruskal Correctness I

Claim 1. Every edge added by Kruskal must be in every MST.

Why?

Kruskal Correctness II

Claim 2. Kruskal produces a spanning tree.

Why?

Conclusion

Theorem. Kruskal’s algorithm produces an MST.

Next Question. How could we implement Kruskal’s algorithm efficiently? What is its running time?

Kruskal’s Algorithm

  Kruskal(V, E, w):
    C <- collection of components
      initially, each vertex is own component
    F <- empty collection
    # iterate in order of increasing weight
    for each edge e = (u, v) in E 
      if u and v are in different components then
        add (u, v) to F
        merge components containing u and v
      endif
    endfor
    return F

Costly Operations

1. Get edges in order of increasing weight
2. Determine if $u$ and $v$ are in same component
3. Merge two components

Maintaining Components

Idea. For each component, designate a leader

• leader is a vertex in its component
• maintain an array that stores each vertex’s component’s leader
  • leader[i] = v means that v is leader of i’s component

Question. How to check if vertices i and j are in the same component? Running time?

Merging Components

Question. How to merge two components?

Merging Components Efficiently?

For each leader, maintain list of vertices in its component.

Merging Strategy

When merging components with leaders $u$ and $v$, new leader is leader of larger component

Claim. If $x$ is relabeled $k$ times, then $x$’s component has size at least $2^k$.

Consequence

Claim. If $x$ is relabeled $k$ times, then $x$’s component has size at least $2^k$.

Consequence 1. If $x$’s component has size $\ell$, then $x$ was relabeled at most $\log \ell$ times.

Conclusion

Theorem. Kruskal’s algorithm can be implemented to run in time $O(m \log n)$ in graphs with $n$ vertices and $m$ edges.

Next Time

• Interval Scheduling (recorded lecture)