Lecture 18: Minimum Spanning Trees

COSC 311 Algorithms, Fall 2022

$ \def\compare{ {\mathrm{compare}} } \def\swap{ {\mathrm{swap}} } \def\sort{ {\mathrm{sort}} } \def\insert{ {\mathrm{insert}} } \def\true{ {\mathrm{true}} } \def\false{ {\mathrm{false}} } \def\BubbleSort{ {\mathrm{BubbleSort}} } \def\SelectionSort{ {\mathrm{SelectionSort}} } \def\Merge{ {\mathrm{Merge}} } \def\MergeSort{ {\mathrm{MergeSort}} } \def\QuickSort{ {\mathrm{QuickSort}} } \def\Split{ {\mathrm{Split}} } \def\Multiply{ {\mathrm{Multiply}} } \def\Add{ {\mathrm{Add}} } \def\cur{ {\mathrm{cur}} } \def\gets{ {\leftarrow} } $

Announcements

Midterms
- should finish grading tomorrow
- pick up in class Wednesday or OH on Thursday
No class on Monday 10/24
- reading + recorded lecture instead

Overview

Minimum Spanning Tree Problem
Prim’s Algorithm

Last Time: Dijkstra’s Algorithm

Single Source Shortest Paths

Input
- graph $G = (V, E)$
- edge weights/lengths $w$
- starting vertex $u$
Output
- (weighted) distance $d[v] = d_w(u, v)$ for every vertex $v$

Dijkstra’s Algorithm:

maintain set $S$ of finalized nodes
greedily choose $v \in V - S$ with minimum $d[v]$
- finalize $v$
- update $d[x]$ for each neighbor $x$ of $v$

DPW in Königsberg

Winter is coming to Königsberg!

Must prepare the bridges for ice
Each bridge has an associated cost to de-ice
Königsberg doesn’t have the budget to de-ice all bridges
For public safety, must ensure that all landmasses are reachable from each other

Question. How to find the cheapest set of bridges to de-ice that maintain connectivity?

Picture

Graph Problem

Input:

a weighted graph $G = (V, E)$ with edge weights $w$

Output:

a set $F$ of edges in $E$ such that
1. $(V, F)$ is connected
2. sum of weights of edges in $F$ is minimal among all connected sub-graphs of $G$

The graph $T = (V, F)$ is called a minimum spanning tree of $G$

Example

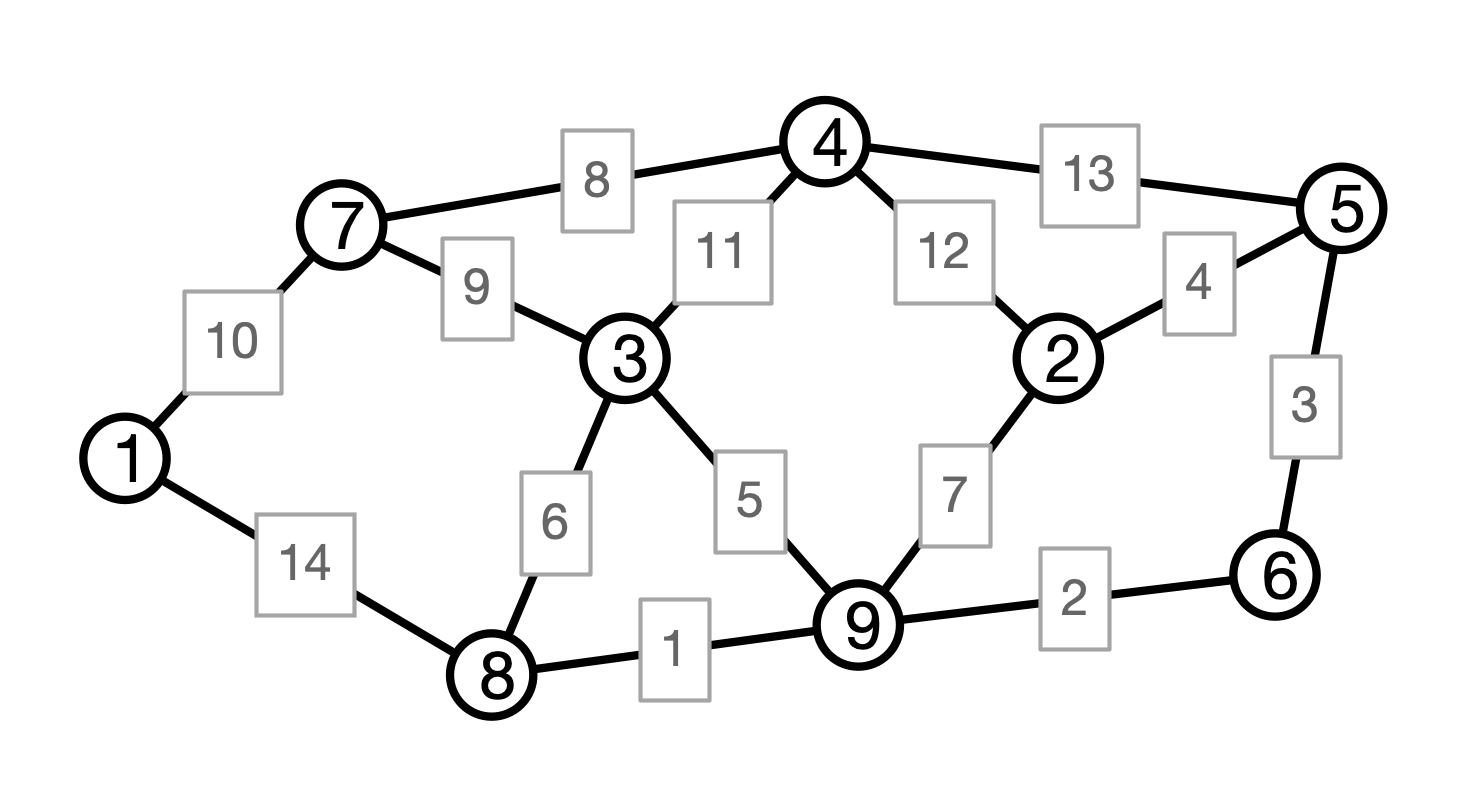
Trees

Recall. A tree $T$ is a graph that:

is connected, and
contains no cycles

MST Problem

Input:

a weighted graph $G = (V, E)$ with edge weights $w$

Output:

a set $F$ of edges in $E$ such that
1. $(V, F)$ is connected
2. sum of weights of edges in $F$ is minimal among all connected sub-graphs of $G$

Question. Why must $T = (V, F)$ be a tree?

A Claim

Claim. Suppose $T$ is an MST for a weighted graph $G$. Then $T$ is a tree.

Proof. Argue by contradiction.

Suppose $T$ is not a tree
By definition of MST, $T$ is connected
So $T$ must contain a cycle $C$

Removing any edge $e$ from $C$ results in a smaller spanning “tree”
$\implies T$ was not minimal, a contradiction

An Idea

Grow a tree outward from a seed vertex:

start with $u$
repeat until we get a spanning tree:
- pick a new edge $e$ to add to our tree

Question. How should we pick the “next” edge?

Tree Growing Example

Question

What information do we need to maintain in order to implement this procedure?

Prim’s Algorithm

  PrimMST(V, E):
    initialize set S = {v} with v arbitrary
    initialize set F = {} of MST edges, priority queue Q
    for each neighbor x of v
      add (v, x) to Q with priority w(v, x)
    while Q is not empty
      (u, v) <- removeMin(Q)
      if S doesn't contain v
        add (u, v) to F
        for each neighbor x of v
          add (v, x) to Q with priority w(v, x)
    return (S, F)

Prim Illustration

Question

Why is graph returned by Prim a tree?

  PrimMST(V, E):
    initialize set S = {v} with v arbitrary
    initialize set F = {} of MST edges, priority queue Q
    for each neighbor x of v
      add (v, x) to Q with priority w(v, x)
    while Q is not empty
      (u, v) <- removeMin(Q)
      if S doesn't contain v
        add (u, v) to F
        for each neighbor x of v
          add (v, x) to Q with priority w(v, x)
    return (S, F)

Another Question

Why is graph returned by Prim a MST?

assume all edge weights are distinct

Must show. Every edge added to $F$ is in an MST.

Cuts in Graphs

Definition. Let $G = (V, E)$ be a graph. A cut in $G$ is a partition of $V$ into two (non-empty) subsets $U$ and $V - U$.

Cuts and MSTs

Cut Claim. Suppose:

$G = (V, E)$ is a weighted graph (with distinct edge weights)
$U, V - U$ a cut in $G$
$T = (V, F)$ an MST
$e = (u, v)$ is the minimum weight edge that crosses the cut
- $u \in U$ and $v \in V - U$

Then:

$T$ contains the edge $e$

Cut Claim Illustration

Prim, Again

  PrimMST(V, E):
    initialize set S = {v} with v arbitrary
    initialize set F = {} of MST edges, priority queue Q
    for each neighbor x of v
      add (v, x) to Q with priority w(v, x)
    while Q is not empty
      (u, v) <- removeMin(Q)
      if S doesn't contain v
        add (u, v) to F
        for each neighbor x of v
          add (v, x) to Q with priority w(v, x)
    return (S, F)

Prim Correctness I

Cut claim $\implies$ Prim produces an MST.

Why?

Consider $k$th edge $e_k$ added by Prim

$S_k = $ contents of $S$ before edge added

What can we say about the cut $S_k, V - S_k$?

Prim Correctness II

First Conclusion. Every edge $e$ added by Prim’s algorithm is in the MST.

Still to show. All MST edges are added.

Why is this so?

Suffices to argue that Prim produces a spanning tree
Set of edges found by Prim form a tree
All vertices of $V$ are in tree (if $G$ is connected)

Conclusion. Prim’s algorithm produces an MST.

Prim Running Time?

  PrimMST(V, E):
    initialize set S = {v} with v arbitrary
    initialize set F = {} of MST edges, priority queue Q
    for each neighbor x of v
      add (v, x) to Q with priority w(v, x)
    while Q is not empty
      (u, v) <- removeMin(Q)
      if S doesn't contain v
        add (u, v) to F
        for each neighbor x of v
          add (v, x) to Q with priority w(v, x)
    return (S, F)

Conclusion

Prim’s algorithm:

computes an MST in $G$
if efficient priority queue is used, running time is $O(m \log n)$

Prim’s algorithm is greedy

to grow a tree, always add the lightest outgoing edge

Next Time

Another greedy MST algorithm!