Lecture 15: Graphs and Distances
COSC 311 Algorithms, Fall 2022
$ \def\compare{ {\mathrm{compare}} } \def\swap{ {\mathrm{swap}} } \def\sort{ {\mathrm{sort}} } \def\insert{ {\mathrm{insert}} } \def\true{ {\mathrm{true}} } \def\false{ {\mathrm{false}} } \def\BubbleSort{ {\mathrm{BubbleSort}} } \def\SelectionSort{ {\mathrm{SelectionSort}} } \def\Merge{ {\mathrm{Merge}} } \def\MergeSort{ {\mathrm{MergeSort}} } \def\QuickSort{ {\mathrm{QuickSort}} } \def\Split{ {\mathrm{Split}} } \def\Multiply{ {\mathrm{Multiply}} } \def\Add{ {\mathrm{Add}} } \def\cur{ {\mathrm{cur}} } $
Overview
- Single Source Shortest Paths
- Depth First Search
- Weighted Graphs
- Weighted Shortest Paths
More Bridges
Gephyrophobia = fear of bridges
Question. How to get from one landmass to another, crossing the fewest possible number of bridges?
Strategy
Find shortest (fewest hops) route by:
- find all vertices reachable in 1 hop
- find all vertices reachable in 2 hops
- find all vertices reachable in 3 hops
- …
Continue until destination is found
Illustration
Graph Distances
Definition. $G = (V, E)$ a graph, $u, v \in V$ vertices. The graph distance between $u$ and $v$, denoted $d(u, v)$, is the length of the shortest path from $u$ to $v$ in $G$.
Example
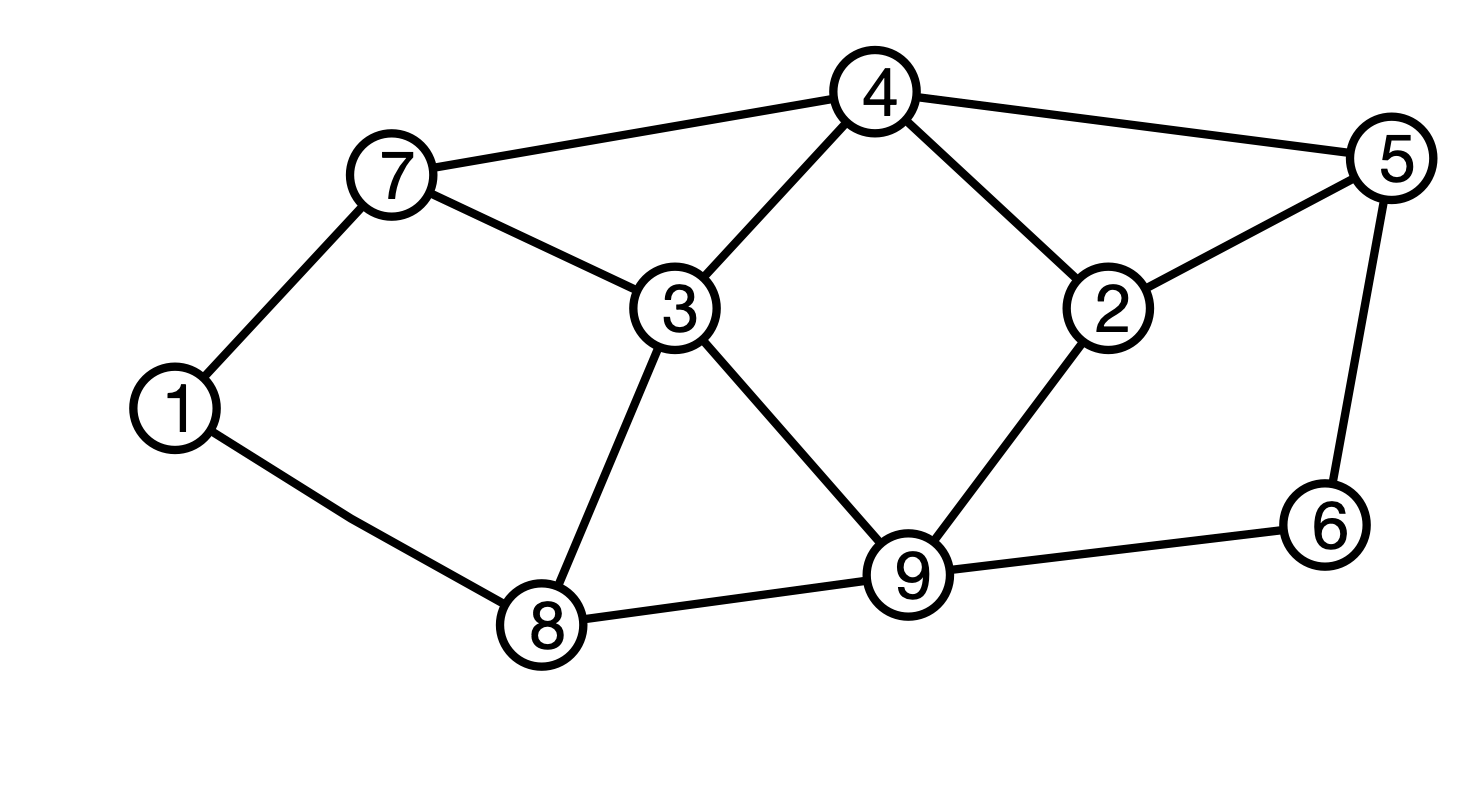
What is $d(1, 3)$? What is $d(1, 5)$?
Single Source Shortest Paths (SSSP)
Unweighted version
Input.
- a Graph $G = (V, E)$
- an initial vertex $u \in V$
- each vertex $v \in V$ has associated adjacency list
- list of $v$’s neighbors
Output.
-
A map $d_u: V \to \{-1, 0, 1, 2, \ldots\}$ such that $d_u(v) = d(u, v)$ is the graph distance from $u$ to $v$
- $d[v] = -1$ indicates no path from $u$ to $v$
Example

BFS Solution
Breadth-First Search
- start at $u$
- examine $u$’s neighbors, at distance $1$
- examine $u$’s neighbors’ neighbors, at distance $2$
- $\vdots$
Greedily examine closest vertices that have not yet been examined…
Queues
Abstract data type (ADT)
- stores elements
- two basic operations
-
add(x)adds elementxto queue -
remove()removes and returns element
-
- FIFO: first in, first out
BFS Pseudocode
BFS(V, E, u):
intialize d[v] <- -1 for all v
d[u] <- 0
queue.add(u)
while queue is not empty do
v <- queue.remove()
for each neighbor w of v do
if d[w] = -1 then
d[w] <- d[v] + 1
queue.add(w)
return d
BFS Illustration
BFS Correctness
Theorem. When BFS(V, E, u) terminates, for every vertex $v \in V$, $d[v]$ stores the distance (minimum number of hops) from $u$ to $v$.
Analysis. Break $V$ into layers
- $L_0$ contains only $u$
- $L_1$ contains neighbors of $u$
- $L_2$ contains neighbors of neighbors of $u$
- $\vdots$
- $L_k$ contains vertices not in $L_0, \ldots, L_{k-1}$ but with at least one neighbor in $L_{k-1}$
Layered Illustration

More Formally
For $i = 0, 1, 2, \ldots$, Define $L_i$ by
- $L_0 = \{u\}$
- $L_i = $ vertices not in $L_0, L_1, \ldots, L_{i-1}$ that have at least one neighbor in $L_{i-1}$
Claim. $L_i$ contains precisely the vertices in $V$ at distance $i$ from $u$.
Analysis of BFS
To Show
- procedure finds vertices in increasing order of distance
- distances are correctly computed when vertex is found (added to queue)
Idea. Break execution of BFS into phases
- phase $i$ starts when first element of $L_i$ is added to queue
- phase $i$ ends when last element in $L_i$ is added to queue
Phase Illustration
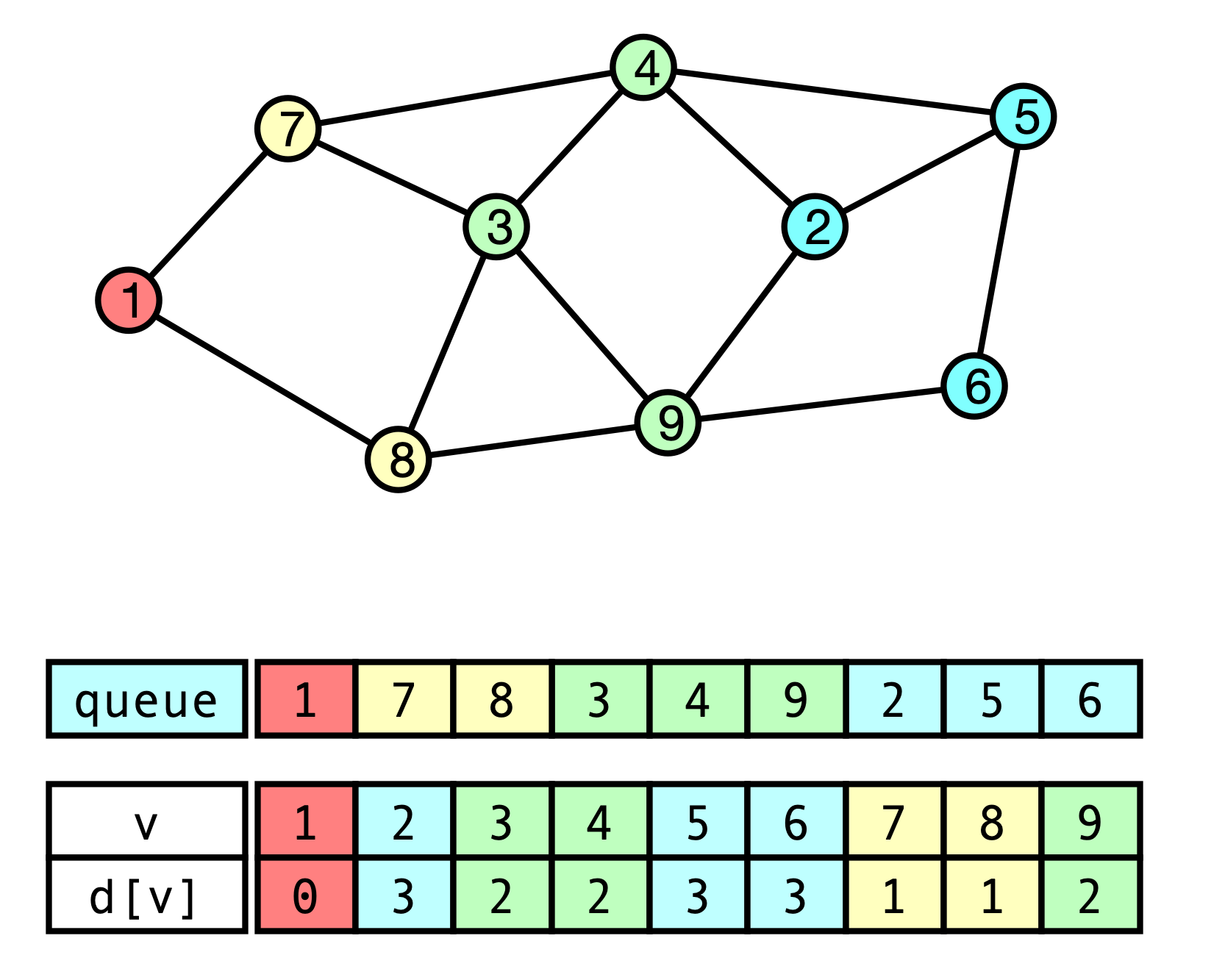
Phase Claim
Claim. Consider an execution of BFS procedure. Then for every phase $i$:
- phase $i$ ends before phase $i+1$ begins
- every vertex from $L_i$ is added to the queue in phase $i$
- each vertex $v$ added in phase $i$ has $d[v] = i$
Proof. Use induction on $i$
Base case $i = 0$. $u$ is the only element in $L_0$, and it is added before any other elements, and $d[u]$ is initialized to $0$.
Inductive Step of Phase Claim
Suppose claim holds for $j \leq i$ (inductive hypothesis). Then:
- when phase $i$ ends (1) all vertices from $L_i$ are in queue and (2) no vertex in $L_{i+1}$ is in queue
- start removing elements in $L_i$ from queue
- when $v$ in $L_i$ is removed, any neighbors in $L_{i+1}$ are added to queue (if not already)
- distance is set to $d[v] \leftarrow i+1$
- every $v$ in $L_{i+1}$ has neighbor in $L_i$
- $\implies$ all $v \in L_{i+1}$ are added to queue when last $L_i$ vertex is removed from queue
- no vertex in $L_{i+2}$ added to queue to this point
Conclusion
BFS(V, E, u):
intialize d[v] <- -1 for all v
d[u] <- 0
queue.add(u)
while queue is not empty do
v <- queue.remove()
for each neighbor w of v do
if d[w] = -1 then
d[w] <- d[v] + 1
queue.add(w)
return d
BFS procedure correctly computes all distances from $u$!
What is Running Time of BFS?
BFS(V, E, u):
intialize d[v] <- -1 for all v
d[u] <- 0
queue.add(u)
while queue is not empty do
v <- queue.remove()
for each neighbor w of v do
if d[w] = -1 then
d[w] <- d[v] + 1
queue.add(w)
return d
More General Problem
Definition. A weighted graph is a graph $G(V, E)$ where each edge $e \in E$ is additionally assigned a (real valued) weight $w(e)$.
- for now, assume $w(e) \geq 0$
Examples.
- weights = distances (not just number of hops)
- weights = cost of connection
- weights = latency of connection
- …
Distance in Weighted Graphs
-
$G = (V, E)$ a graph, $w$ weights
-
$P = v_0 e_1 v_1 e_2 v_2 \cdots e_k v_k$ a path
-
The (weighted) length of $P$ is
\[w(P) = w(e_1) + w(e_2) + \cdots + w(e_k)\]
Example
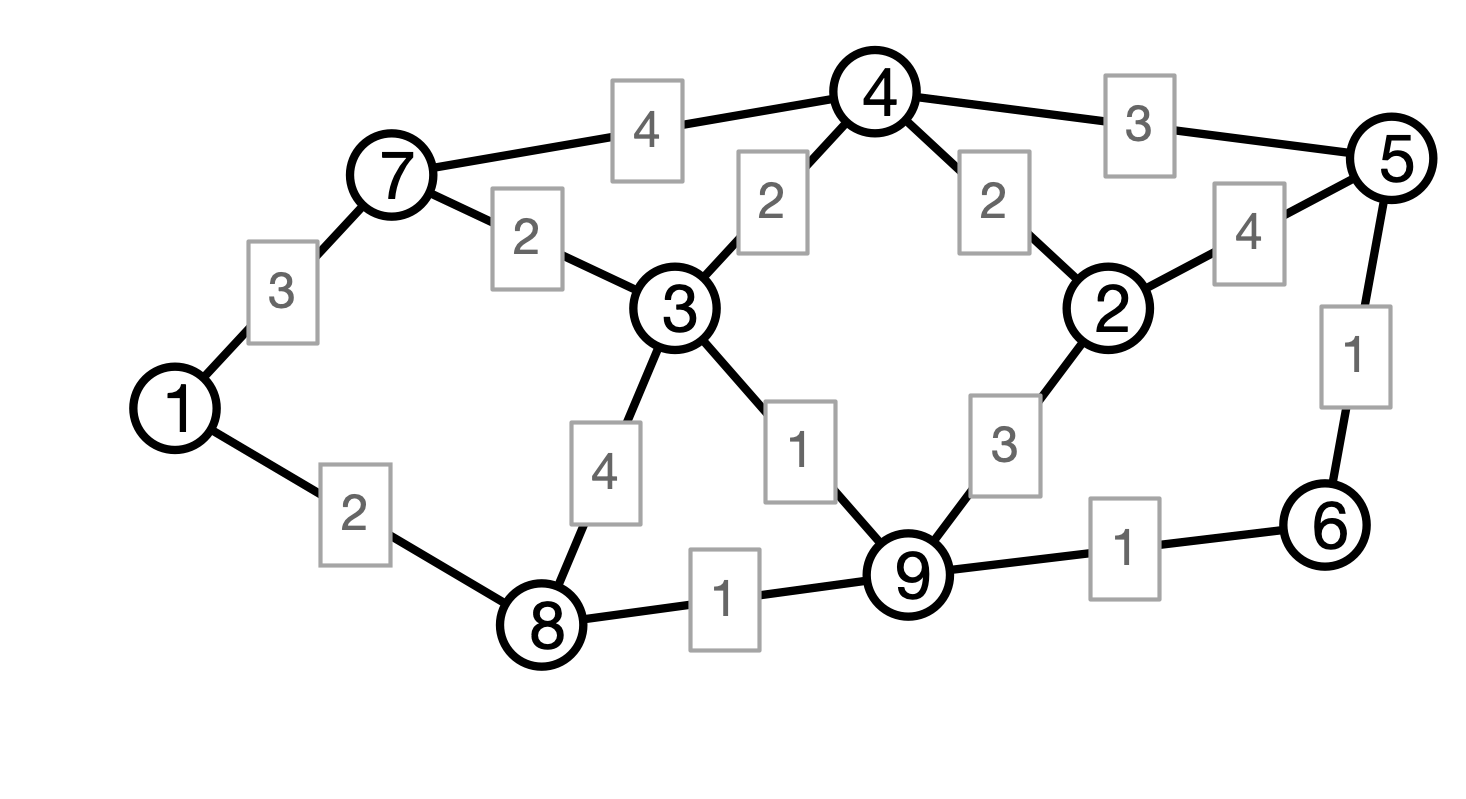
Weighted Shortest Paths
Given weights $w$, define $d_w(u, v)$ to be minimum (weighted) length of any path $P$ from $u$ to $v$.
Example

What is $d_w(1, 3)$? What about $d_w(1, 5)$?
Weighted SSSP
Input.
- a weighted Graph $G = (V, E)$, edge weights $w$
- an initial vertex $u \in V$
- each vertex $v \in V$ has associated adjacency list
- list of $v$’s neighbors
- includes weight of edge from $v$ to each neighbor
Output.
-
A map $d_u: V \to \mathbf{R}$ such that $d_u(v) = d(u, v)$ is the graph distance from $u$ to $v$
- $d[v] = \infty$ indicates no path from $u$ to $v$
Weighted SSSP
Does BFS compute weighted distances from $u$?
- must update procedure
- when processing edge $(v, x)$, should updated $d[x] = d[v] + w(v, x)$ rather than setting $d[x] <- d[v] + 1$
Does this work?
Weighted BFS Example
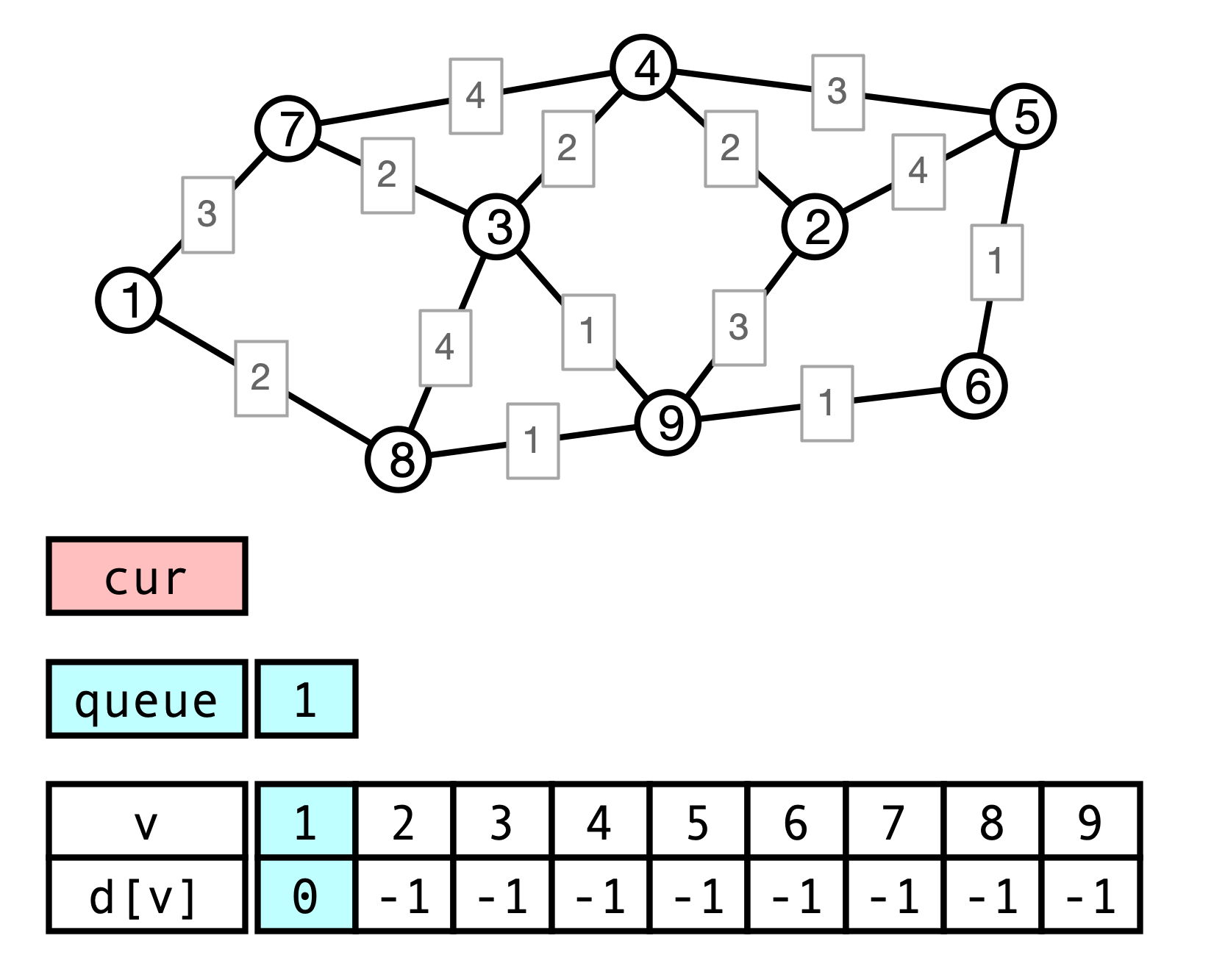
Issue
- BFS processes vertices in order of fewest hops from $u$
- With weighted graphs, shortest path need not have fewest hops
BFS Analysis Takeaway
-
BFS succeeds on unweighted graphs because closer vertices are processed before farther vertices
-
Could we get similar behavior for weighted distances?
-
must ensure: vertices processed in order of weighted distance from $u$
-
how can we do this?
-
-
How could we efficiently implement a modified procedure?
Next Time
Dijkstra’s Algorithm