Lecture 12: Maximization

COSC 311 Algorithms, Fall 2022

$ \def\compare{ {\mathrm{compare}} } \def\swap{ {\mathrm{swap}} } \def\sort{ {\mathrm{sort}} } \def\insert{ {\mathrm{insert}} } \def\true{ {\mathrm{true}} } \def\false{ {\mathrm{false}} } \def\BubbleSort{ {\mathrm{BubbleSort}} } \def\SelectionSort{ {\mathrm{SelectionSort}} } \def\Merge{ {\mathrm{Merge}} } \def\MergeSort{ {\mathrm{MergeSort}} } \def\QuickSort{ {\mathrm{QuickSort}} } \def\Split{ {\mathrm{Split}} } \def\Multiply{ {\mathrm{Multiply}} } \def\Add{ {\mathrm{Add}} } $

Overview

Recurring Recurrences
Maximizing Profit

Last Time

The “Master Theorem”

Given recurrence $T(n) = a T(n / b) + f(n)$
Define $c = \log_b a$
Three cases:
1. If $f(n) = O(n^d)$ for $d < c$ then $T(n) = O(n^c)$
2. If $f(n) = \Theta(n^c \log^k n)$ then $T(n) = O(n^c \log^{k+1} n)$
3. If $f(n) = \Omega(n^d)$ for $d > c$, then $T(n) = O(f(n))$

A Technical Note

In formal statement we have

$T(n) = a T(n / b) + f(n)$

In practice, might have

$T(n) = a T(\lceil n / b \rceil) + f(n)$

The conclusion of the theorem still holds in this case!

Master Theorem for Binary Search

$T(n) = a T(n / b) + f(n)$

  BinarySearch(a, val, i, j):
    if j = i then return false
    if j - i = 1 then return (a[i] = val)
    m <- (j + i) / 2
    if a[m] > val then
      return BinarySearch(a, val, i, m)
    else
      return BinarySearch(a, val, m, j)
    endif

Master Theorem for MergeSort

$T(n) = a T(n / b) + f(n)$

MergeSort(a, i, j):
  if j - i = 1 then
    return
  endif
  m <- (i + j) / 2
  MergeSort(a,i,m)
  MergeSort(a,m,j)
  Merge(a,i,m,j)

Profit Maximization

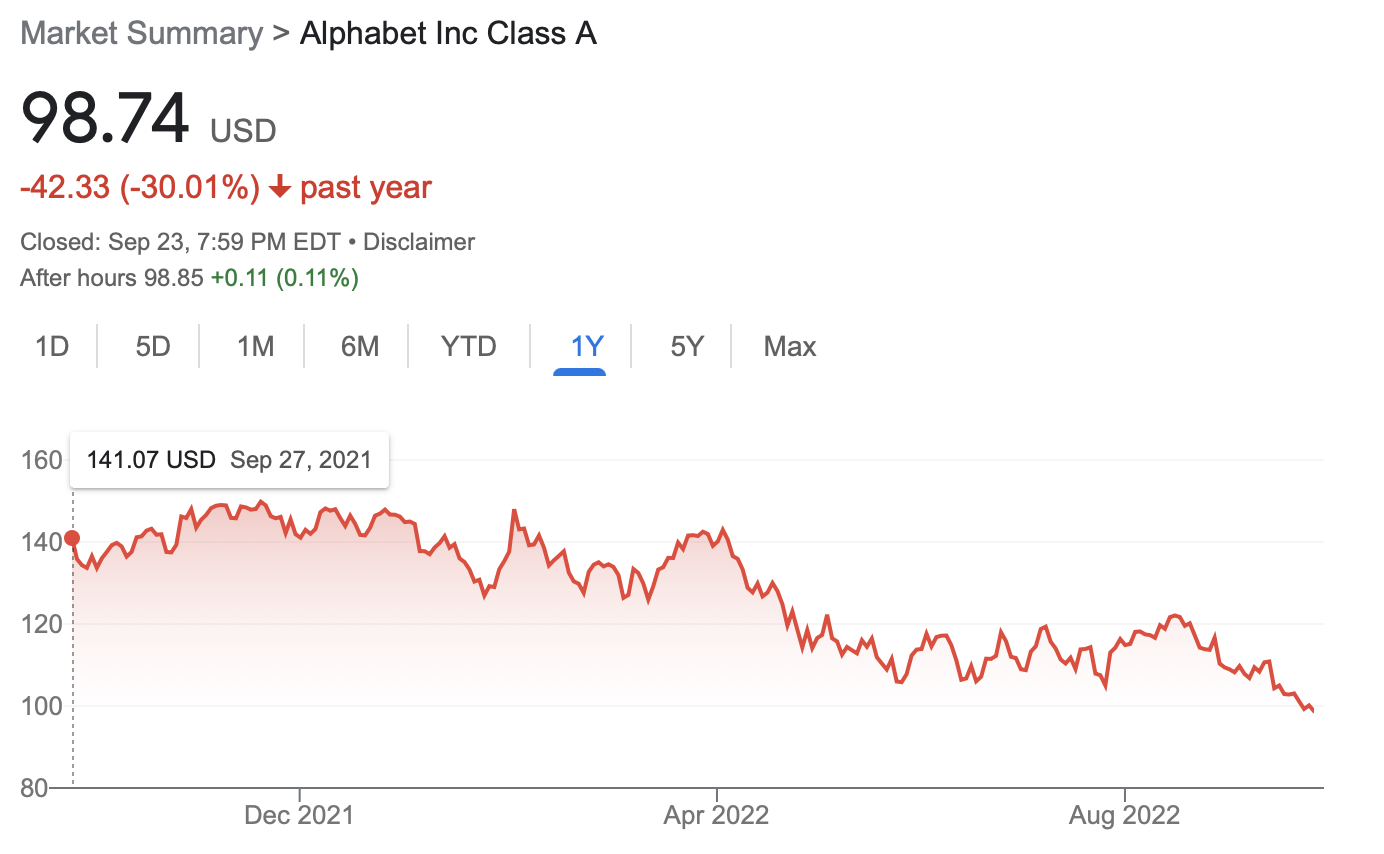
Goal. Pick day $b$ to buy and day $s$ to sell to maximize profit.

Formalizing the Problem

Input. Array $a$ of size $n$

$a[i] = $ price of Alphabet stock on day $i$

Output. Indices $b$ (buy) and $s$ (sell) with $1 \leq b \leq s \leq n$ that maximize profit

$p = a[s] - a[b]$

Simple Procedure

Devise a procedure to determine max profit in time $O(n^2)$.

Divide and Conquer?

Question. Can we compute maximum profit faster?

Use divide an conquer?

Maximum Profit via D&C?

Three Cases

Array $a$ of size $n$, midpoint $m = n / 2$

Maximum profit in left half: $b, s < n / 2$
Maximum profit in right half: $n/2 \leq b, s$
Maximum profit splits the halves: $b < n/2 \leq s$

Algorithmic Approach

Find maximum profit in left half
- get value from recursive method call
Find maximum profit in right half
- get value from recursive method call
Find maximum profit for split halves
- how?

Observation

To find the maximum profit for split halves:

find the lowest price $a[b]$ for $b < n/2$
find the highest price $a[s]$ for $s \geq n/2$

Maximum profit is $a[s] - a[b]$.

Maximization Pseudocode

  # find maximum profit achievable for b, s 
  # satisfying i <= b <= s < j

  MaxProfit(a, i, j):
    if j - i = 1 then return 0	
    m <- (i + j) / 2	
    left <- MaxProfit(a, i, m)
    right <- MaxProfit(a, m, j)	
    min <- FindMin(a, i, m)
    max <- FindMax(a, m, j)
    return Max(left, right, max - min)

Example

MaxProfit([1, 3, 2, 4], 1, 5)

Algorithm Correctness

Claim. MaxProfit(a, i, j) returns the maximum value of $a[s] - a[b]$ over all $s, b$ satisfying $i \leq b \leq s < j$.

Proof. Argue by induction on $n = j - i =$ size of the call.

  MaxProfit(a, i, j):
    if j - i = 1 then return 0	
    ...

Base case. $n = 1$.

Inductive Step I

  MaxProfit(a, i, j):
    ...
    left <- MaxProfit(a, i, m), right <- MaxProfit(a, m, j)	
    min <- FindMin(a, i, m), max <- FindMax(a, m, j)
    return Max(left, right, max - min)

Claim. MaxProfit(a, i, j) returns the maximum value of $a[s] - a[b]$ over all $s, b$ satisfying $i \leq b \leq s < j$.

Three possible cases…

Inductive Step II

  MaxProfit(a, i, j):
    ...
    left <- MaxProfit(a, i, m), right <- MaxProfit(a, m, j)	
    min <- FindMin(a, i, m), max <- FindMax(a, m, j)
    return Max(left, right, max - min)

Claim. MaxProfit(a, i, j) returns the maximum value of $a[s] - a[b]$ over all $s, b$ satisfying $i \leq b \leq s < j$.

Inductive hypothesis. Claim holds for all sizes $< n$.

Inductive step. Must show claim holds for size $n$.

IH $\implies$ left is max profit in a[i..m-1]
IH $\implies$ right is max profit in a[m..j-1]
max - min is max profit with $b < m \leq s$

Running Time Rercurrence?

$T(n) = a T(n / b) + f(n)$

  # find maximum profit achievable for b, s 
  # satisfying i <= b <= s < j

  MaxProfit(a, i, j):
    if j - i = 1 then return 0	
    m <- (i + j) / 2	
    left <- MaxProfit(a, i, m)
    right <- MaxProfit(a, m, j)	
    min <- FindMin(a, i, m)
    max <- FindMax(a, m, j)
    return Max(left, right, max - min)

Applying Master Theorem

Given recurrence $T(n) = a T(n / b) + f(n)$
Define $c = \log_b a$
Three cases:
1. If $f(n) = O(n^d)$ for $d < c$ then $T(n) = O(n^c)$
2. If $f(n) = \Theta(n^c \log^k n)$ then $T(n) = O(n^c \log^{k+1} n)$
3. If $f(n) = \Omega(n^d)$ for $d > c$, then $T(n) = O(f(n))$

Exercise

Modify the code to return the indices b and s that maximize profit.

  # find maximum profit achievable for b, s 
  # satisfying i <= b <= s < j

  MaxProfit(a, i, j):
    if j - i = 1 then return 0	
	m <- (i + j) / 2	
	left <- MaxProfit(a, i, m)
	right <- MaxProfit(a, m, j)	
	min <- FindMin(a, i, m)
	max <- FindMax(a, m, j)
	return Max(left, right, max - min)