Lecture 11: Solving Recurrences

COSC 311 Algorithms, Fall 2022

$ \def\compare{ {\mathrm{compare}} } \def\swap{ {\mathrm{swap}} } \def\sort{ {\mathrm{sort}} } \def\insert{ {\mathrm{insert}} } \def\true{ {\mathrm{true}} } \def\false{ {\mathrm{false}} } \def\BubbleSort{ {\mathrm{BubbleSort}} } \def\SelectionSort{ {\mathrm{SelectionSort}} } \def\Merge{ {\mathrm{Merge}} } \def\MergeSort{ {\mathrm{MergeSort}} } \def\QuickSort{ {\mathrm{QuickSort}} } \def\Split{ {\mathrm{Split}} } \def\Multiply{ {\mathrm{Multiply}} } \def\Add{ {\mathrm{Add}} } $

Announcements

Midterm 10/07

Yes, there will be a makeup exam the following week
Midterm guide posted next weekend

Overview

Finishing Multiplication
Solving Recurrences
Maximizing Profit

Last Time

Gradeschool multiplication in binary
Less intuitive multiplication

Multiplication via Divide and Conquer

Idea. Break numbers up into parts

Assume $a$ and $b$ are both represented with $n = 2B$ bits, $n$ power of $2$
Write:
- $a = a_1 a_0 = a_1 2^B + a_0$
- $b = b_1 b_0 = b_1 2^B + b_0$
Then:
\[\begin{align*} a b &= (a_1 2^B + a_0)(b_1 2^B + b_0)\\ &= a_1 b_1 2^{2B} + (a_1 b_0 + a_0 b_1) 2^B + a_0 b_0 \end{align*}\]

The Trick

With $a b = a_1 b_1 2^{2B} + (a_1 b_0 + a_0 b_1) 2^B + a_0 b_0$
Compute:
- $c_2 = a_1 b_1$
- $c^* = (a_1 + a_0)(b_1 + b_0)$
- $c_0 = a_0 b_0$
Then:
\[a b = c_2 2^{2B} + (c^* - c_2 - c_0) 2^B + c_0\]

Conclusion. Each a multiplication of size $n$ can be computed using $3$ multiplications of size $n/2$ and $O(1)$ addition/subtractions/shifts.

Karatsuba Multiplication

  KMult(a, b):
    n <- size(a) (= size(b))
    if n = 1 then return a*b
	a = a1 a0
	b = b1 b0
	c2 <- KMult(a1, b1)
	c0 <- KMult(a0, b0)
	c <- KMult(a1 + a0, b1 + b0)
	return (c2 << n) + ((c - c2 - c0) << (n/2)) + c0

Karatsuba Recursion Tree

Efficiency of Karatsuba

At depth $k$:

$3^k$ calls to KMult
size of each call is $n / 2^k$
depth of recursion is $\log n$

Total running time:

$O(n) + \frac 3 2 O(n) + \left( \frac 3 2\right)^2 O(n) + \cdots + \left(\frac 3 2 \right)^{\log n} O(n)$

Can show:

This expression is $O(3^{\log n})$

Simplify:

Final Running Time

Result. The running time of Karatsuba multiplication is $O(n^{\log 3}) \approx O(n^{1.58})$

when $n$ is reasonbly large, $n^{1.58} \ll n^2$
E.g., $1,000^2 = 1,000,000$ vs $1,000^{1.58} \approx 55,000$

Recent Progress on Multiplication

Theorem (Harvey and ven der Hoeven, 2019). It is possible to multiply two $n$ bit numbers in time $O(n \log n)$.

See Mathematicians Discover the Perfect Way to Multiply from Quanta Magazine
Main technique: “Fast Fourier Transform,” a divide-and-conquer algorithm

Conditional lower bound (Afshani et al., 2019). Multiplying two $n$ bit numbers requires $\Omega(n \log n)$ time, unless the “network coding conjecture” is false.

Recurrence Relation

Running time of Karatsuba multiplication $T(n)$

  KMult(a, b):
    n <- size(a) (= size(b))
    if n = 1 then return a*b
	a = a1 a0
	b = b1 b0
	c2 <- KMult(a1, b1)
	c0 <- KMult(a0, b0)
	c <- KMult(a1 + a0, b1 + b0)
	return (c2 << n) + ((c - c2 - c0) << (n/2)) + c0

Running time satisfies recurrence relation
\[T(n) = 3 T(n / 2) + O(n)\]
Recurrence of this form satisfies $T(n) = O(n^{\log 3})$

More General Recurrences

General form of recurrences
\[T(n) = a T(n / b) + f(n)\]
Interpretation for D&C
- Divide problem into $a$ parts
- Each part has size $n/b$
- Time to combine solutions is $f(n)$

General Solutions

The “Master Theorem”

$T(n) = a T(n / b) + f(n)$
Define $c = \log_b a$
Three cases:
1. If $f(n) = O(n^d)$ for $d < c$ then $T(n) = O(n^c)$
2. If $f(n) = \Theta(n^c \log^k n)$ then $T(n) = O(n^c \log^{k+1} n)$
3. If $f(n) = \Omega(n^d)$ for $d > c$, then $T(n) = O(f(n))$

A Technical Note

In formal statement we have

$T(n) = a T(n / b) + f(n)$

In practice, might have

$T(n) = a T(\lceil n / b \rceil) + f(n)$

The conclusion of the theorem still holds in this case!

Master Theorem for Karatsuba

$T(n) = a T(n / b) + f(n)$

  KMult(a, b):
    n <- size(a) (= size(b))
    if n = 1 then return a*b
	a = a1 a0
	b = b1 b0
	c2 <- KMult(a1, b1)
	c0 <- KMult(a0, b0)
	c <- KMult(a1 + a0, b1 + b0)
	return (c2 << n) + ((c - c2 - c0) << (n/2)) + c0

Master Theorem for Binary Search

$T(n) = a T(n / b) + f(n)$

  BinarySearch(a, val, i, j):
    if j = i then return false
    if j - i = 1 then return (a[i] = val)
    m <- (j + i) / 2
    if a[m] > val then
      return BinarySearch(a, val, i, m)
    else
      return BinarySearch(a, val, m, j)
    endif

Master Theorem for MergeSort

$T(n) = a T(n / b) + f(n)$

MergeSort(a, i, j):
  if j - i = 1 then
    return
  endif
  m <- (i + j) / 2
  MergeSort(a,i,m)
  MergeSort(a,m,j)
  Merge(a,i,m,j)

Profit Maximization

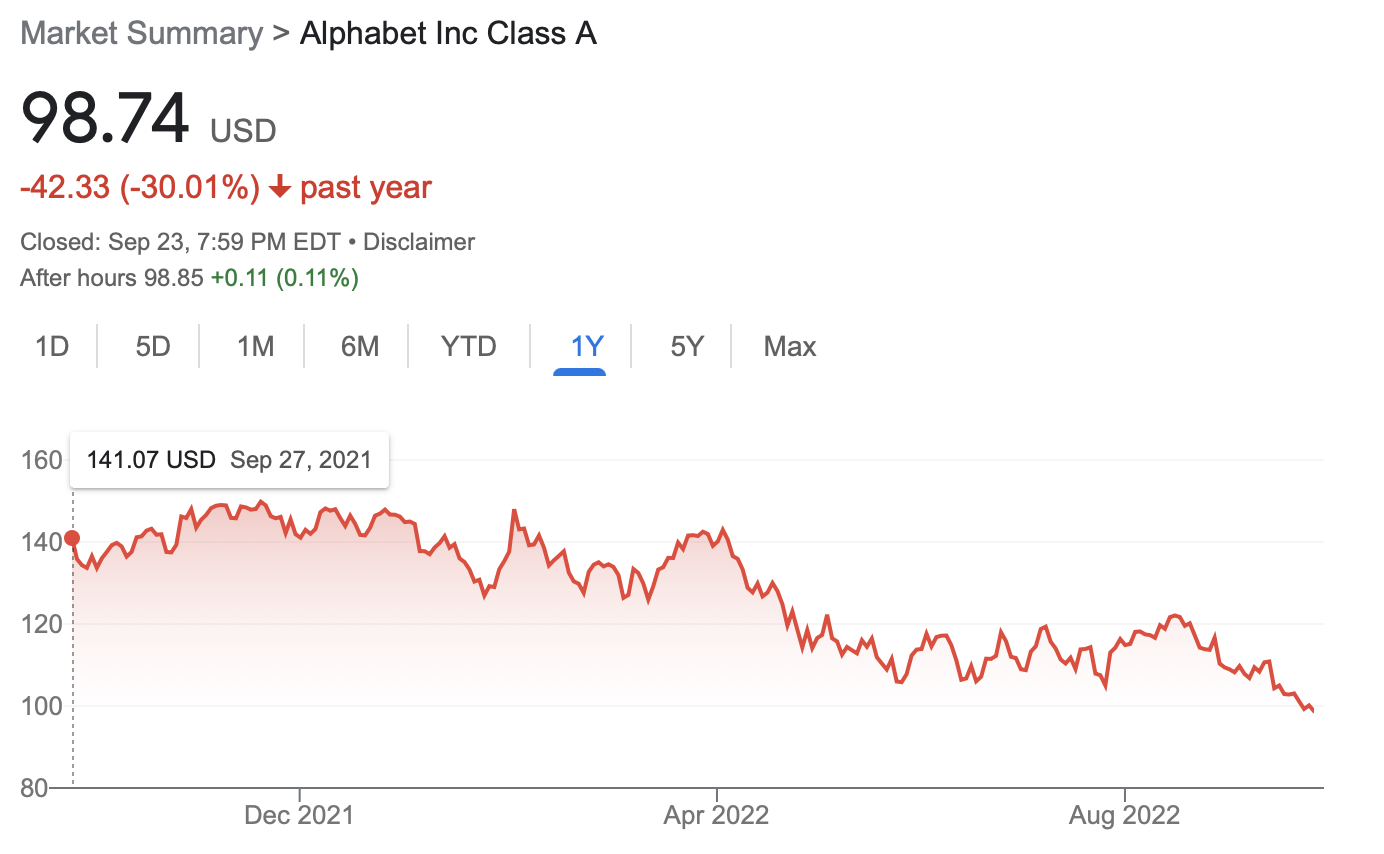
Goal. Pick day $b$ to buy and day $s$ to sell to maximize profit.

Formalizing the Problem

Input. Array $a$ of size $n$

$a[i] = $ price of Alphabet stock on day $i$

Output. Indices $b$ (buy) and $s$ (sell) with $1 \leq b \leq s \leq n$ that maximize profit

$p = a[s] - a[b]$

Simple Procedure

Devise a procedure to determine max profit in time $O(n^2)$.

Divide and Conquer?

Question. Can we compute maximum profit faster?

Use divide an conquer?