Lecture 23: Consensus 1

Mission Critical Components

Suppose you’re designing an airplane

1. Need computers to control everything
   • sensors for speed, thrust, flap positions, pitch, roll, yaw
   • must adjust constantly to fly
2. But computers occasionally (regularly) crash/need restart

How to design around this issue?

Fault-Tolerance through Duplication?

Have multiple duplicate, independent systems

• systems run in parallel
• highly unlikely both crash simultaneously
  • restarts are infrequent
  • restarting one system won’t affect other system

The end of our worries?

Trouble Ahead

Suppose all systems working normally, but

• system 1 says increase thrust
• system 2 says decrease thrust
• system 3 not responding (restart?)

What do we do?

The Problem of Consensus

Have multiple processes with different inputs

• For us, binary inputs
  • 0 = decrease thrust
  • 1 = increase thrust

Goal:

• agree on same output

More Formally

Setup:

• $n$ processes/threads, $P_1, P_2, \ldots, P_n$
• processes have unique IDs, $1, 2, \ldots, n$ (like ThreadId.get())
• each process $i$ holds input $x_i = 0$ or $1$

Output:

• each process $i$ outputs $b_i = 0$ or $1$

Failure:

• Some process(es) may crash
  • failing process may perform some steps before failing
  • cannot distinguish a crashed process from a slow process

Conditions for Consensus

• Agreement: all processes output the same value
• Validity: if all systems have the same input, they all output that value
• Termination: all (non-faulty) processes decide on an output and terminate after a finite number of steps

Exercise

Devise an algorithm for consensus assuming:

1. Fair scheduler
   • every process is scheduled eventually
2. No faulty processes

Consensus with Faults

Suppose some process(es) may crash at any time during an execution…

• Other processes can’t tell that a process crashes
  • e.g., cannot distinguish slow process from crashed

Not Consensus 1

How can we achieve…

• Agreement: all processes output the same value
• Validity: if all systems have the same input, they all output that value
• Termination: all (non-faulty) processes decide on an output and terminate after a finite number of steps

Not Consensus 2

How can we achieve…

• Agreement: all processes output the same value
• Validity: if all systems have the same input, they all output that value
• Termination: all (non-faulty) processes decide on an output and terminate after a finite number of steps

Not Consensus 3

How can we achieve…

• Agreement: all processes output the same value
• Validity: if all systems have the same input, they all output that value
• Termination: all (non-faulty) processes decide on an output and terminate after a finite number of steps

So

Without too much trouble, we can achieve…

• …consensus without faults
• …“consensus” without agreement
• …“consensus” without validity
• …“consensus” without termination

What about consensus with faults?

A Remarkable Fact

Theorem (FLP, 1985). There is no algorithm that achieves consensus in the presence of even a single faulty process.

• Proven by Fischer, Lynch, and Paterson in 1985
  • their version of result for “message passing” model
  • ours is for shared memory
• Surprise to the parallel/distributed computing community
• Among most influential results in CS

Our Plan

Prove version of FLP result:

• There is no wait-free protocol for consensus for any $n > 1$
  • wait-free is stronger assumption than termination

Before going further

• Specify computational model
• Make preliminary observations
• Outline argument

Computational Model

• Processes have shared memory (registers)
• Atomic read/write access
  • behavior like volatile variables in Java
• Scheduler decides which process makes a step
  • assume each step is read/write
• Some processes may crash
  • such a process is never scheduled again
• Scheduler is otherwise fair: non-crashed processes are scheduled eventually

Algorithms

An algorithm $A$ specifies next operation:

• read value from shared register
• write value to shared register
• terminate

as a function of

• input ($x_i$)
• outcomes of previous (read) operations

Next step is uniquely determined by local input and values read in previous steps

Example: Default to 0

Idea: output 0 unless all processes have input 1

int in = getLocalInput();
int i = ThreadId.get();

write(i, in); // write my value to register i

if (in == 0) return 0;

for (int j = 0; j < nProcesses; j++) {
    // wait until register j has been written	
    while (read(j) != 0 && read(j) != 1) { };
	
    if (read(j) == 0) return 0;
}

// all processors have in == 1
return 1;

Executions

An execution $E$ of algorithm $A$ specifies

• Inputs of all processes
• Sequence of steps taken by processes
  • read
  • write
  • terminate
  • crash

Executions may be incomplete

• Not all nodes have terminated/crashed yet
  • encodes current state/history of execution

Executions may be extended by scheduling more steps

Example of Execution $E$

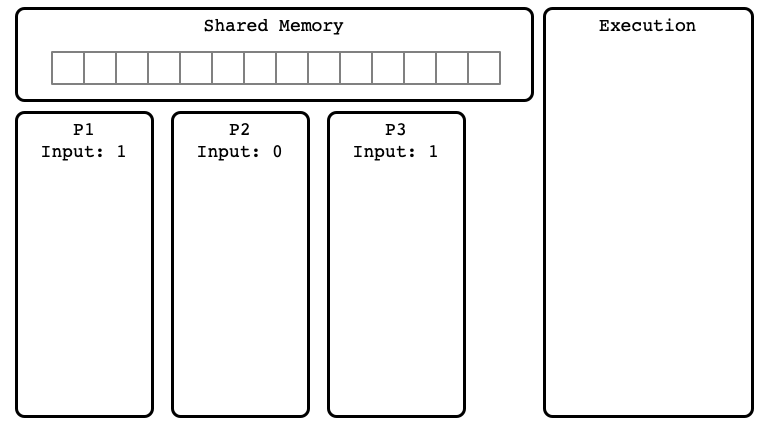
$E$ Step 01

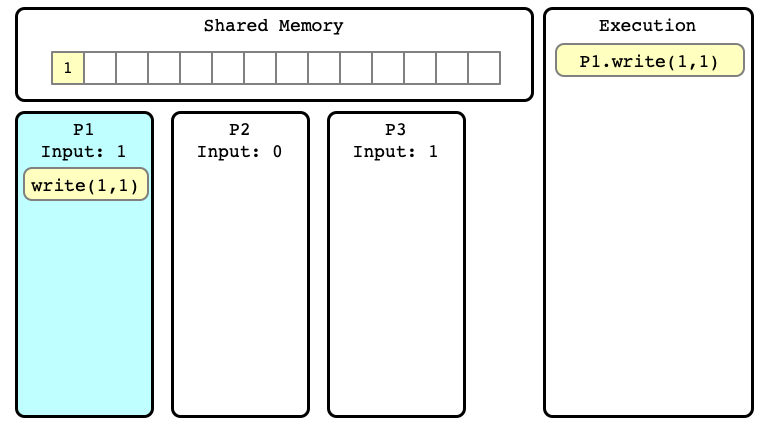
$E$ Step 02

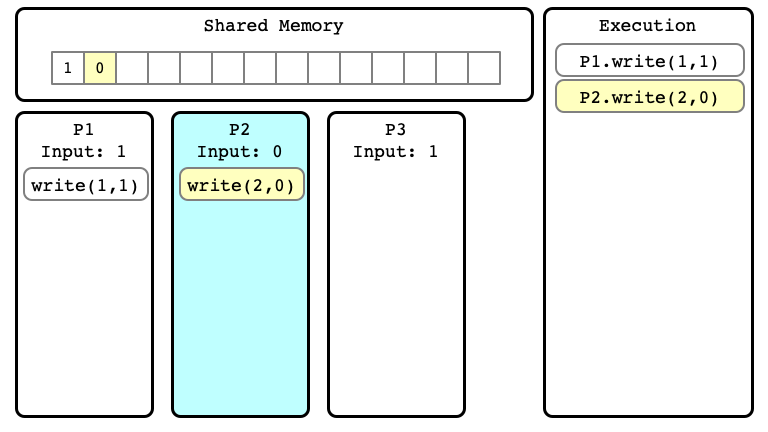
$E$ Step 03

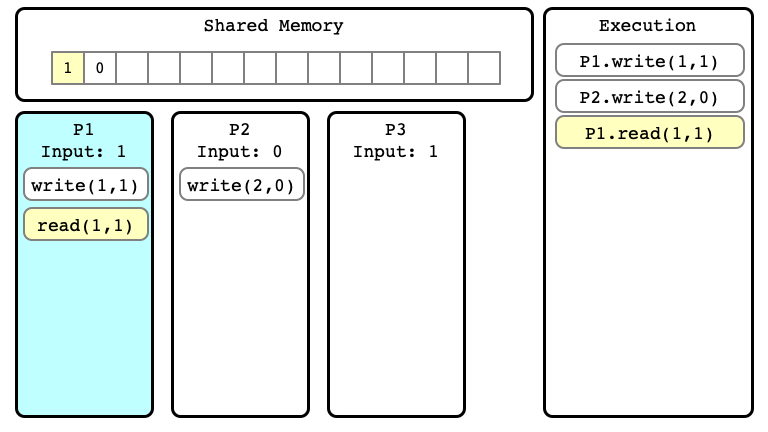
$E$ Step 04

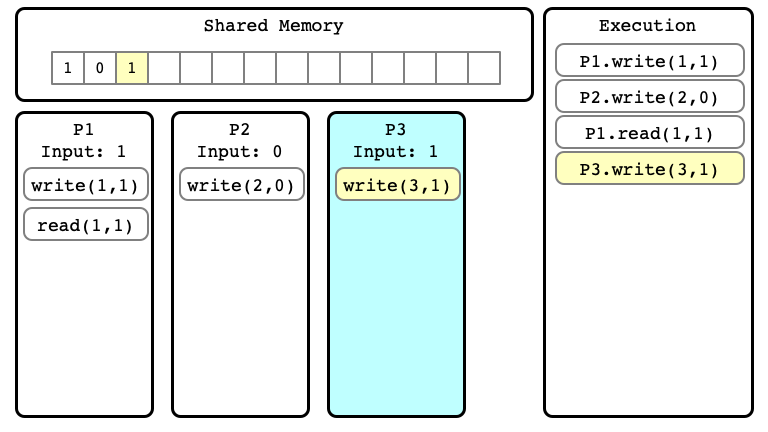
$E$ Step 05

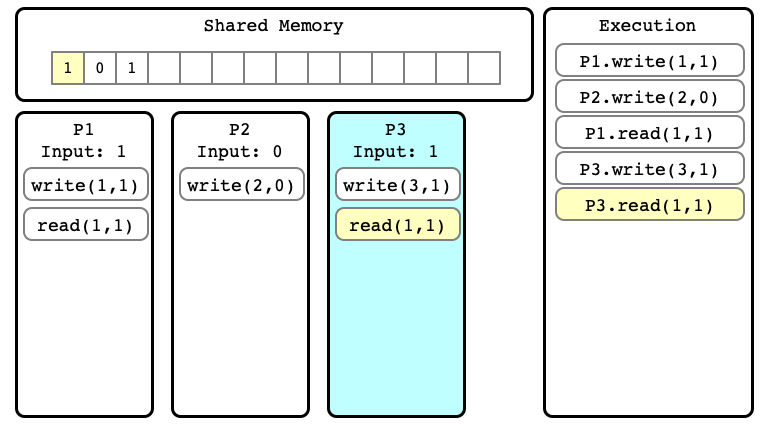
$E$ Step 06

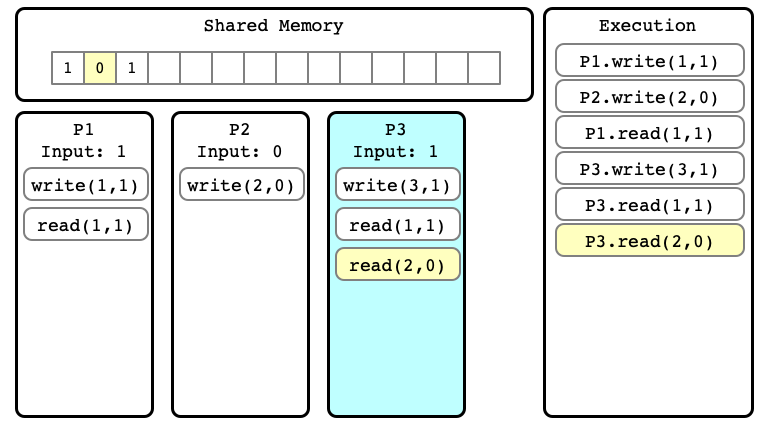
Extending Executions

In $E$, no process has terminated yet

• We can consider extensions of a given execution
• Start with $E$, and perform more steps

$E’$ Step 06

$E’$ Step 07

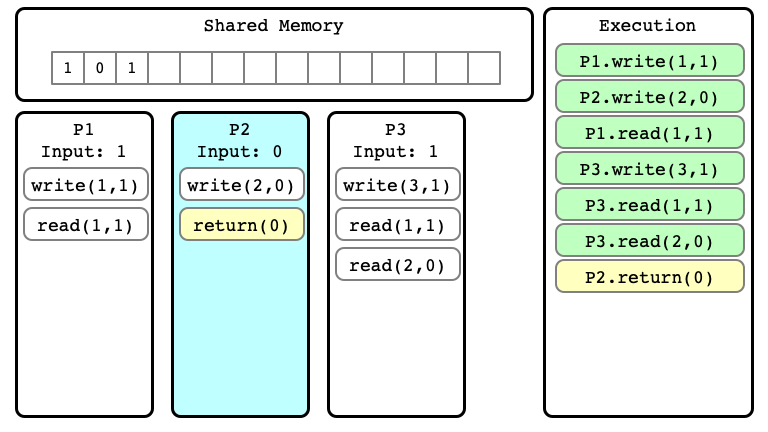
$E’$ Step 08

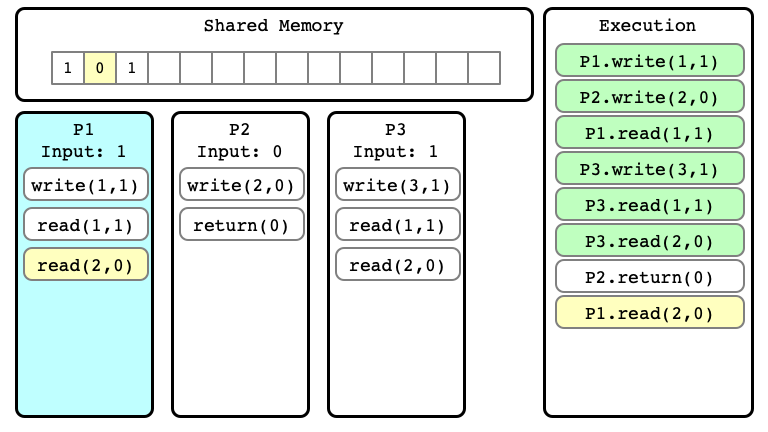
$E’$ Step 09

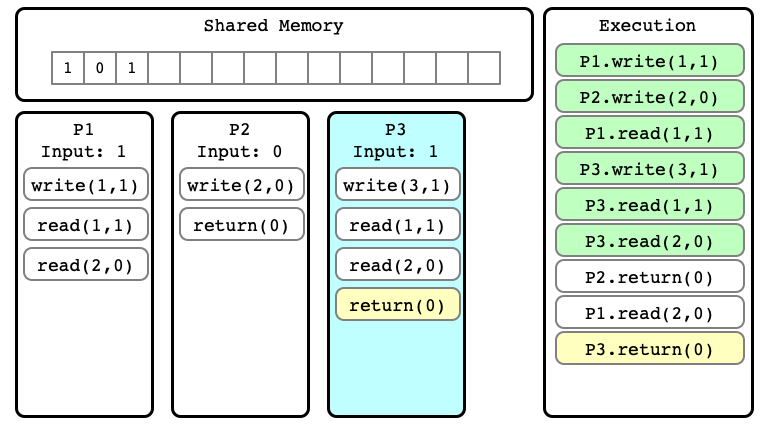
$E’$ Step 10

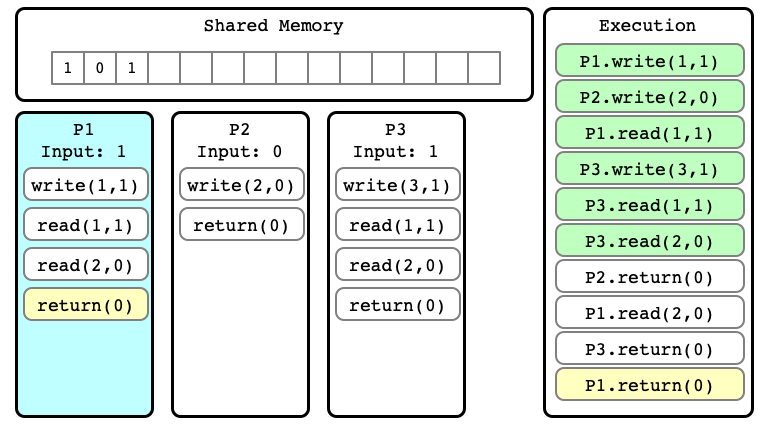
Note

We can consider many different extensions of $E$

Extension $E’$ of $E$

Alternate extension $E’’$

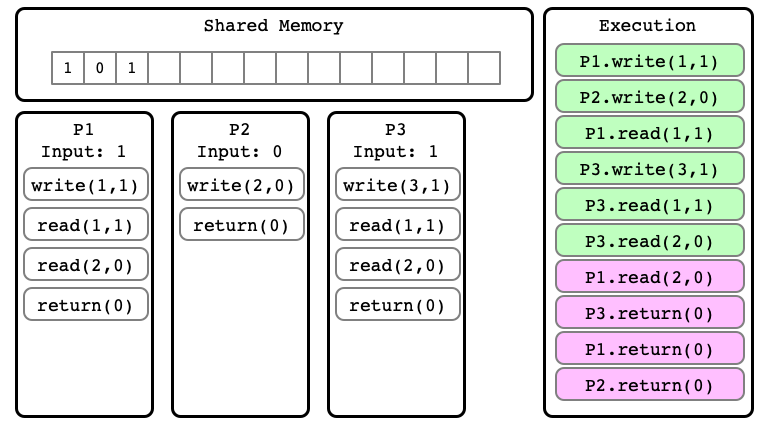
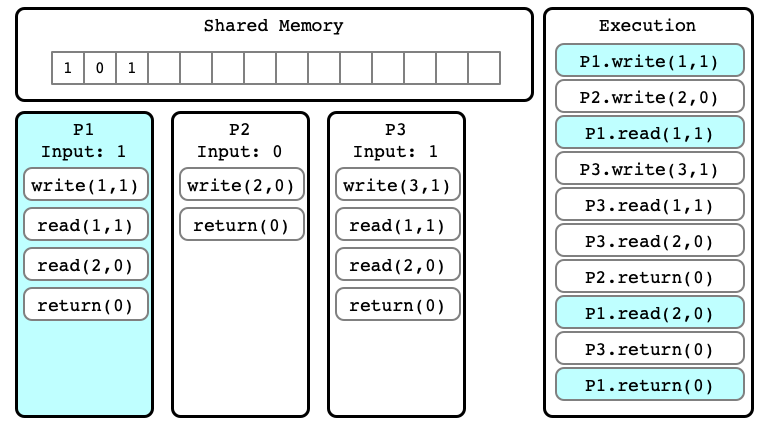
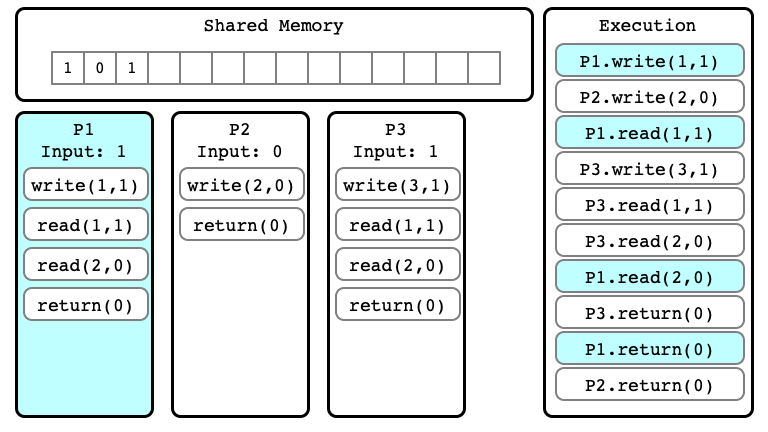
Indistinguishable Executions

• $E$ and $E’$ are executions
• they are indistinguishable at process $P_i$ if in $E$ and $E’$:
  1. $P_i$ has same input
  2. sequence of read/write operations performed by $P_i$ are same
  3. the sequence of values read and written by $P_i$ are the same

$E’$ for P1

$E’’$ for P1

First Important Observation

Lemma 1. If executions $E$ and $E’$ are indistinguishable to process $P_i$ then:

1. If $P_i$ has not yet terminated, then $P_i$’s next step will be the same in any extension
2. If $P_i$ has terminated, then $P_i$’s output is the same in $E$ and $E’$

Bivalent Executions

• Consider a (hypothetical) wait-free consensus protocol $A$
• Let $E$ be an execution of $A$

We say that $E$ is…

1. $0$-valent if in every extension of $E$, all processes output $0$
2. $1$-valent if in every extension of $E$, all processes output $1$
3. bivalent if there exist
   • an extension $E’$ of $E$ in which all processes output $0$
   • an extension $E’’$ of $E$ in which all processes output $1$

Second Important Observation

Lemma 2. Suppose $A$ solves consensus. Then there is a bivalent initial state.

• Here an initial state is an execution in which no process has yet taken a step
  • the execution consists of only inputs for each process

Proof of Lemma 2

Must show: there is a bivalent initial state

Argument:

• by contradiction: suppose no bivalent initial state
• consider sequence of initial states
• show some are $0$-valent, some are $1$-valent
• show that some must be bivalent

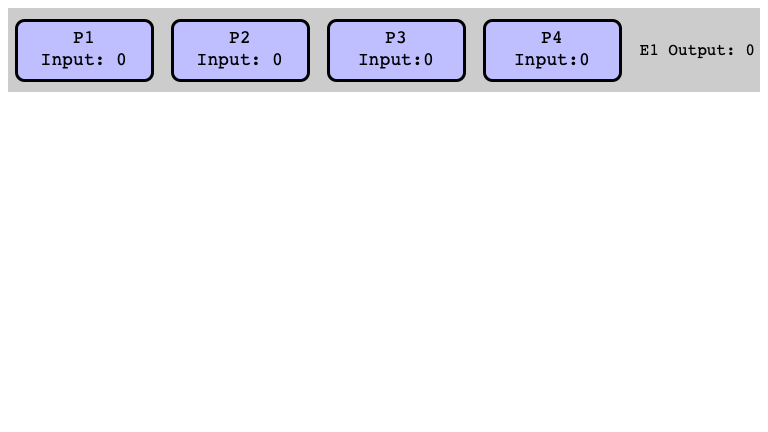
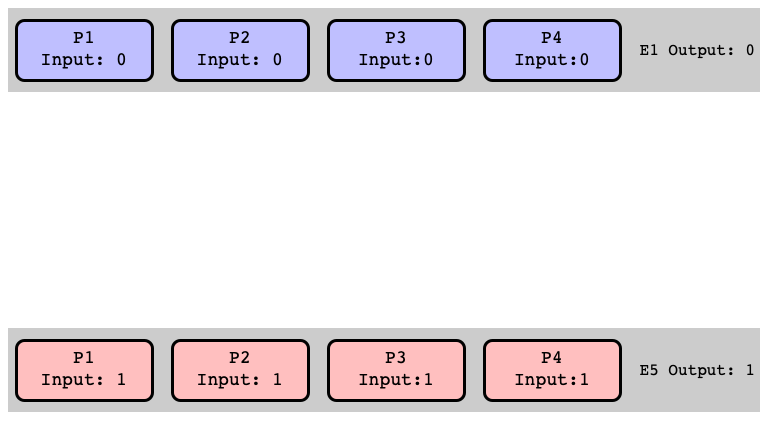
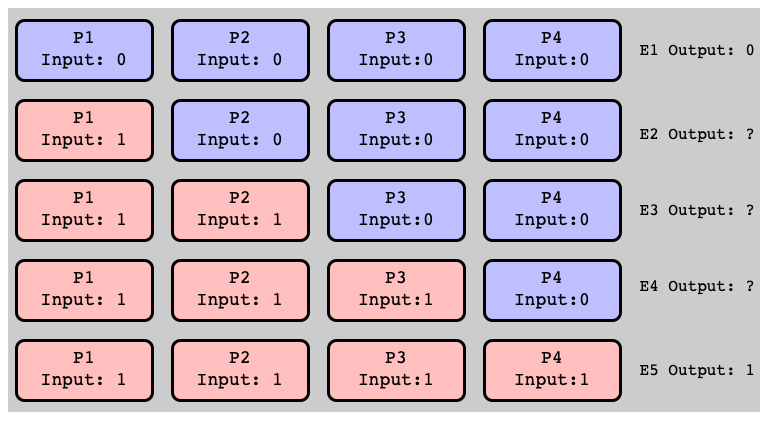
$E_1$ is $0$-valent (Why?)

$E_5$ is $1$-valent

More Initial States

Assume: All Univalent

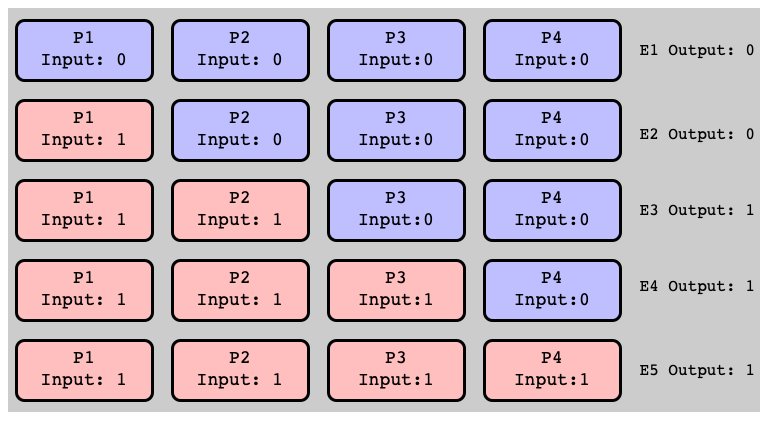
Adjacent Pair, Different Valency

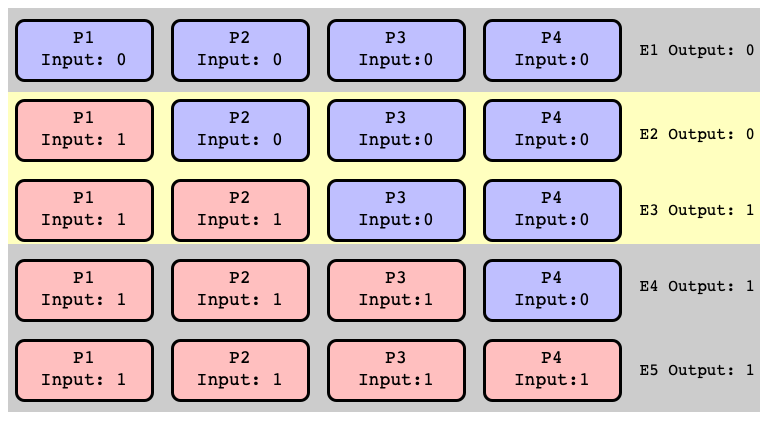
All Extensions of $E_2$ Return $0$

All Extensions of $E_3$ Return $1$

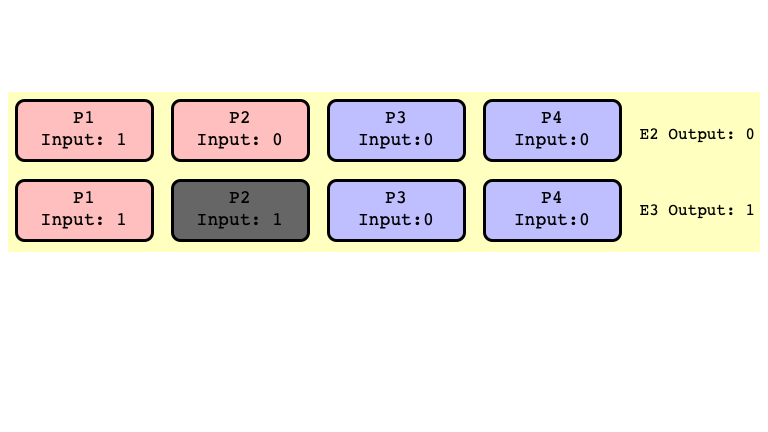
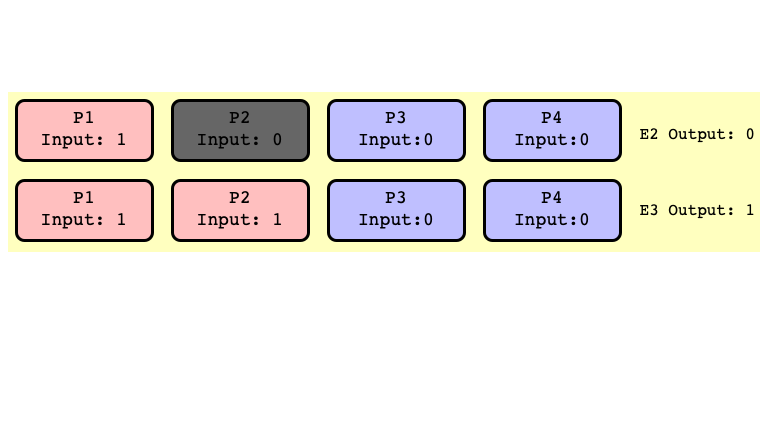
$E_2’$ and $E_3’$ Indistinguishable

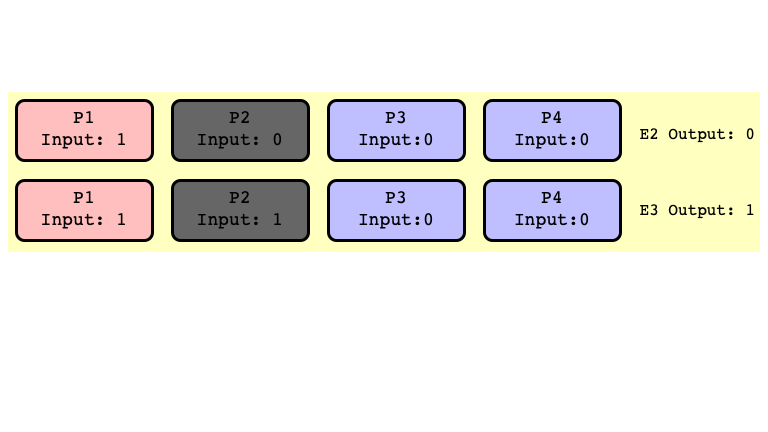
$E_2$ and $E_3$ Bivalent

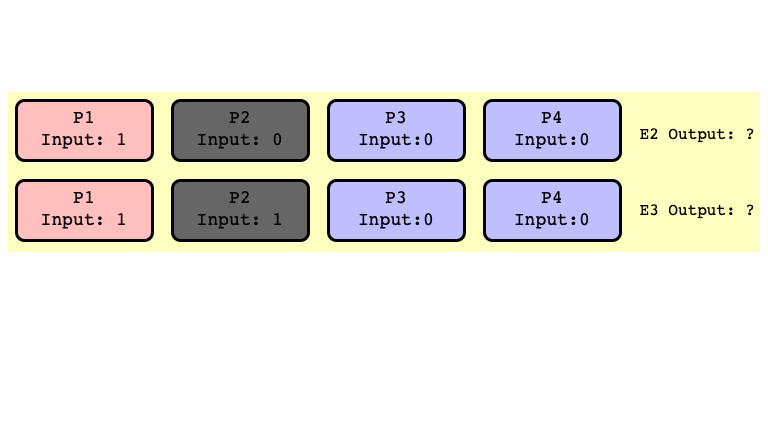
Note

Don’t need to assume $P_2$ crashes

• just assume first step of $P_2$ is scheduled after some other thread outputs
• this is possible because we assume $A$ is wait-free
  • some process guaranteed to terminate even if one is not scheduled

Mere possibility of a crash together with wait-free assumption implies existence a bivalent initial state

• same holds if we require only termination with one fault

Next Time

• Bivalent initial conditions have critical executions
• Wait-free consensus is impossible!
  • assuming only read/write registers…