Lecture 22: Concurrent Stacks

Overview

1. Concurrent Stacks
2. Elimination
3. Consensus

Last Time

Concurrent Queues:

1. Unbounded with locks
2. Unbounded lock-free
3. Bounded with locks

Download and test the code yourself:

• ConcurrentQueues.zip

Today: The Stack

Basic operations

• void push(T item) add a new item to the top of the stack
• T pop() remove top item from the stack and return it
  • throw EmptyException if stack was empty

Linked List Implementation

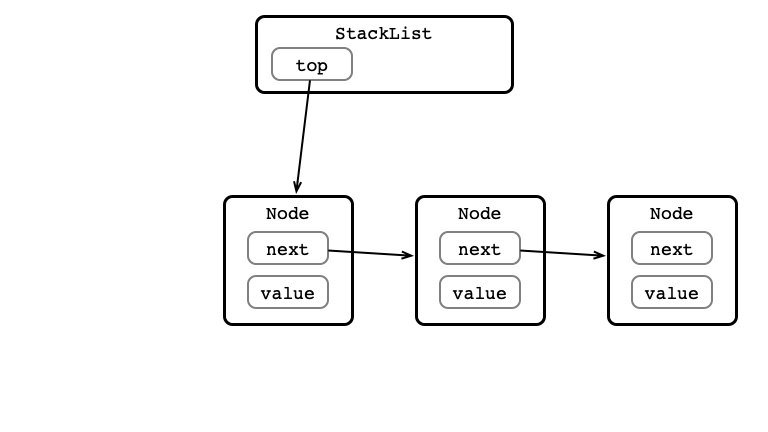
push() Step 1: Create Node

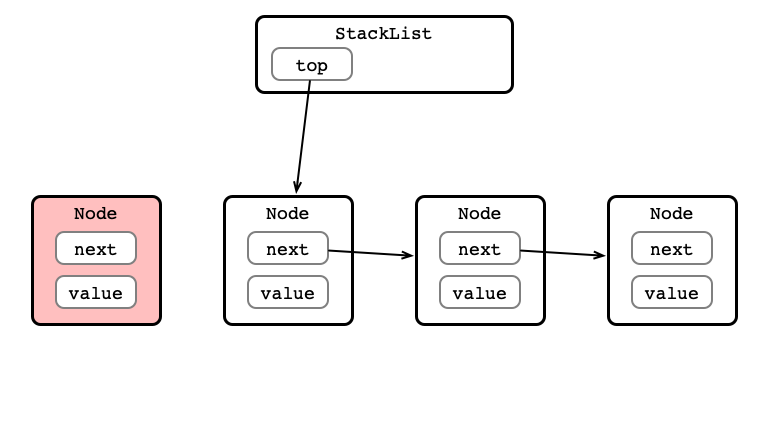
push() Step 2: Set next

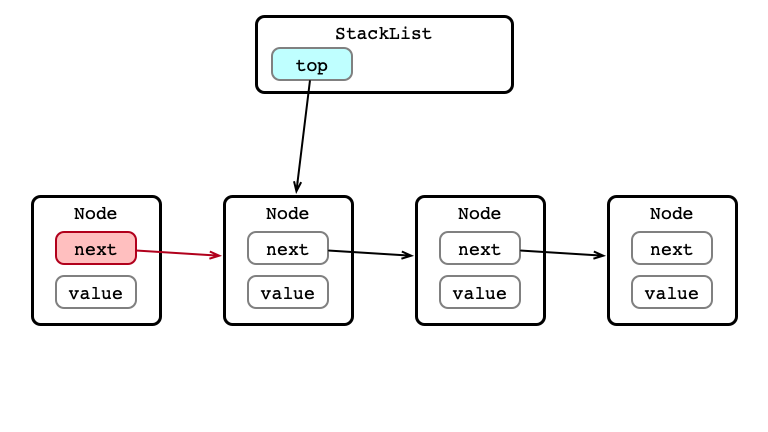
push() Step 3: Set head

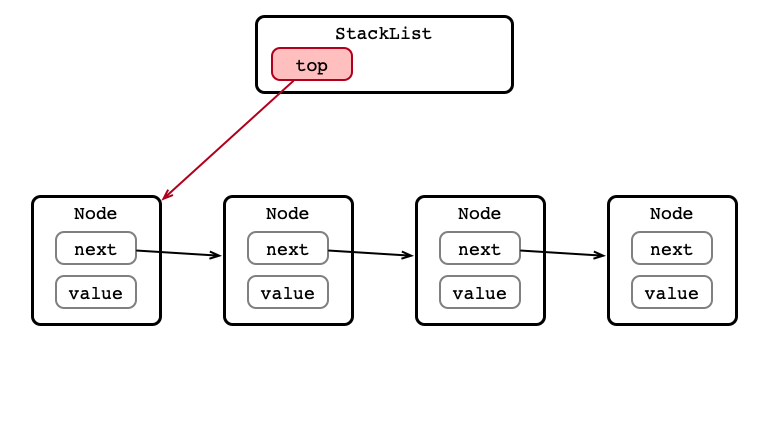
push() Complete

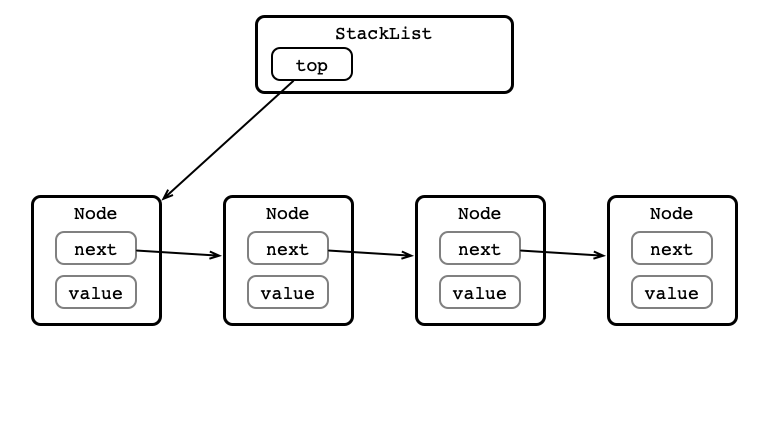
pop()?

pop() Step 1: Store value

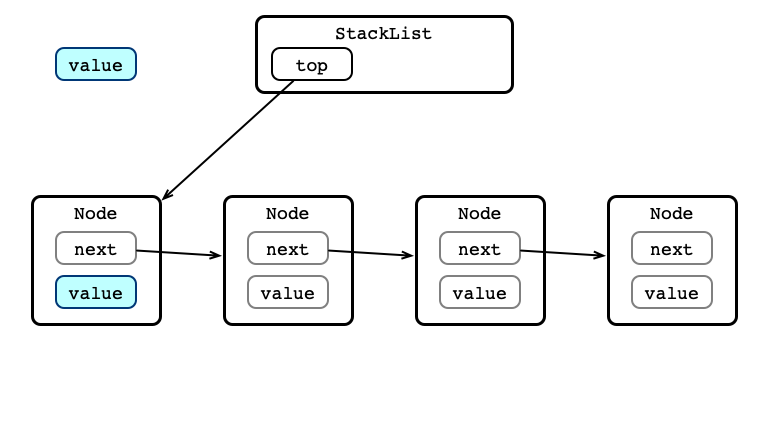
pop() Step 2: Update head

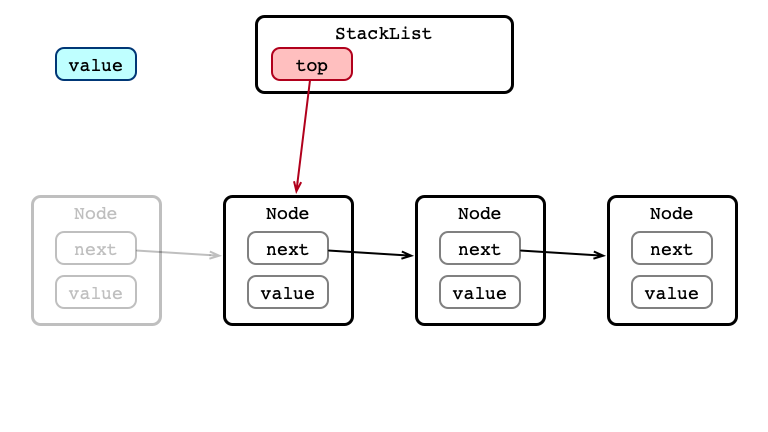
pop() Step 3: Return value

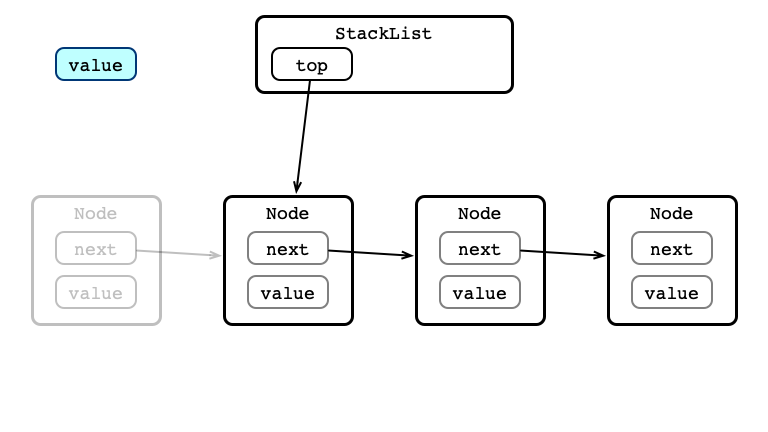
Concurrent Stack

With locks:

• Since all operations modify head, coarse locking is natural choice

Without locks?

A Lock-free Stack

Use linked-list implementation

• Logic is simpler than queues’ because all operations affect same node
• Idea:
  • store top as an AtomicReference<Node>
  • use compareAndSet to modify top
    • success, or retry
• Unlike queue:
  • item on top of stack precisely when top points to item’s Node

Implementing the Lock-Free Stack

public class LockFreeStack<T> implements SimpleStack<T> {
    AtomicReference<Node> top = new AtomicReference<Node>(null);

    public void push(T item) {...}

    public T pop() throws EmptyException {...}
    
    class Node {
	public T value;
	public AtomicReference<Node> next;
    
	public Node(T value) {
	    this.value = value;
	    this.next  = new AtomicReference<Node>(null);
	}
    }    

}

Implementing push

    public void push(T item) {
	
	Node nd = new Node(item);
	Node oldTop = top.get();
	nd.next.set(oldTop);
	
	while (!top.compareAndSet(oldTop, nd)) {
	    oldTop = top.get();
	    nd.next.set(oldTop);	    
	}
    }

Implementing pop

    public T pop() throws EmptyException {
	while (true) {
	    Node oldTop = top.get();
	    
	    if (oldTop == null) {
		throw new EmptyException();
	    }

	    Node newTop = oldTop.next.get();

	    if (top.compareAndSet(oldTop, newTop)) {
		return oldTop.value;
	    }
	}
    }

Sequential Bottleneck

Modifying top

• No matter how many threads, push/pop rate limited by top.compareAndSet(...)
• This seems inherent to any stack…

… or is it?

Elimination

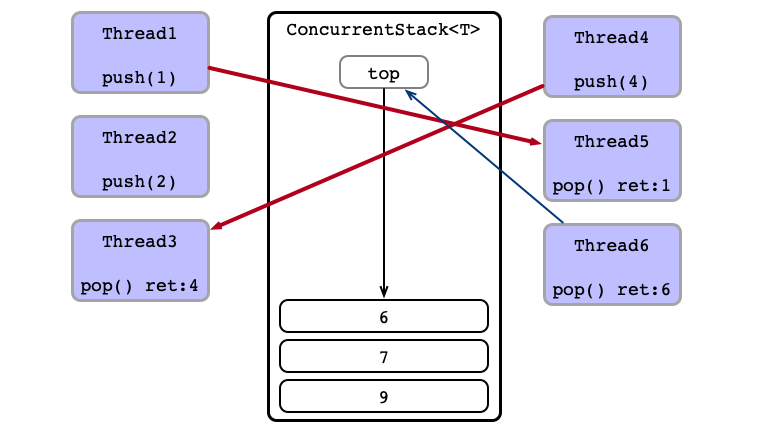
Consider several concurrent accesses to a stack:

• T1 calls stk.push(item1)
• T2 calls stk.push(item2)
• T3 calls stk.pop()
• T4 calls stk.push(item4)
• T5 calls stk.pop()
• T6 calls stk.pop()

Trick Question. What is the state of stk after these calls? What do pop calls return?

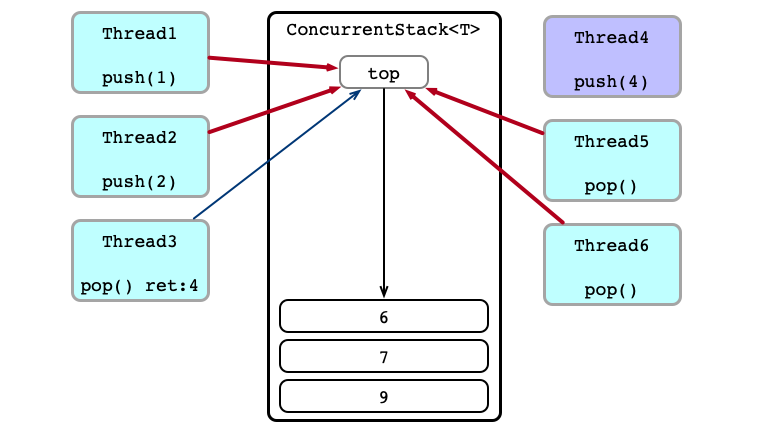
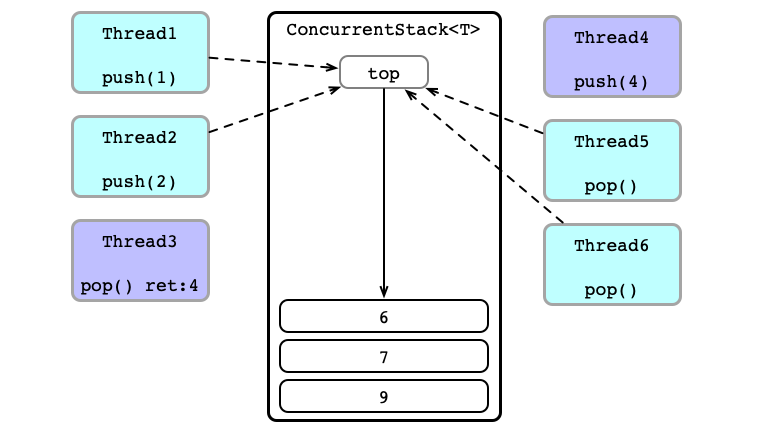
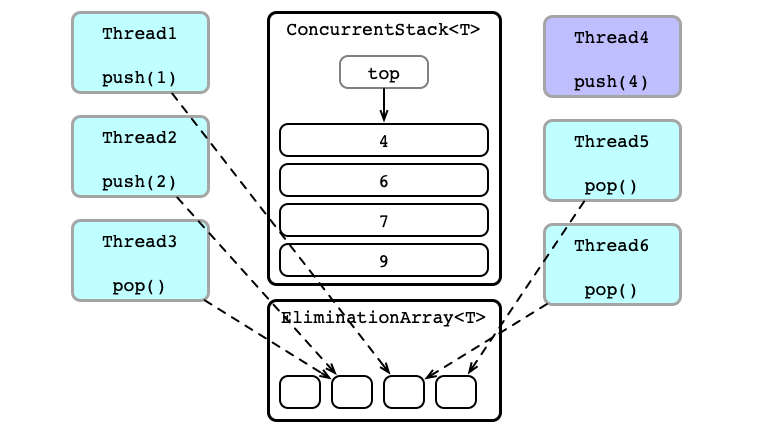
Concurrent Calls

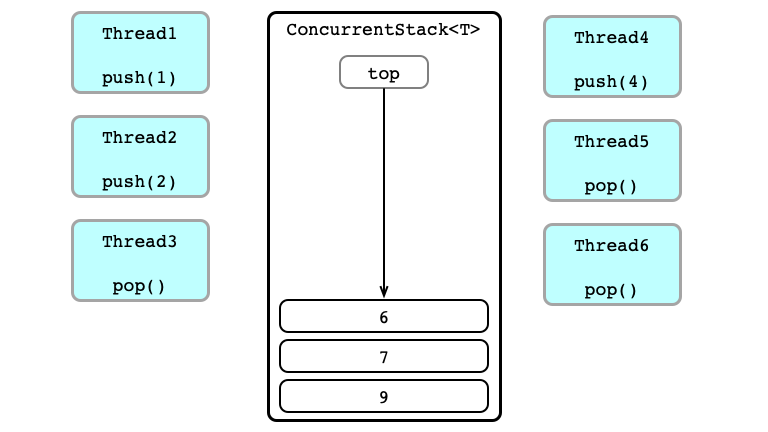
Contention!

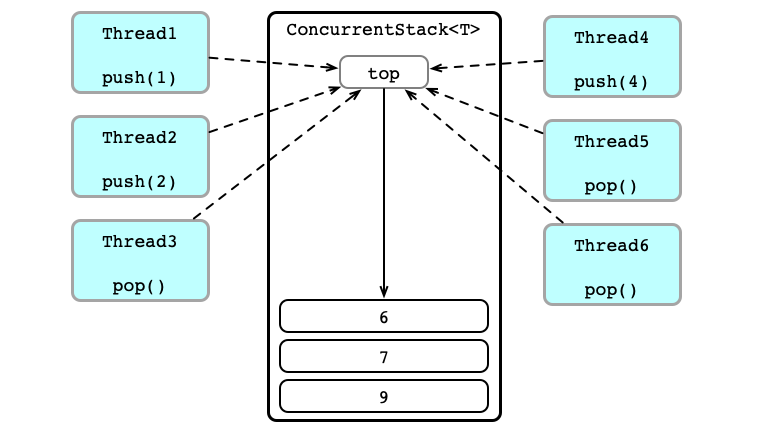
Thead 4 Wins

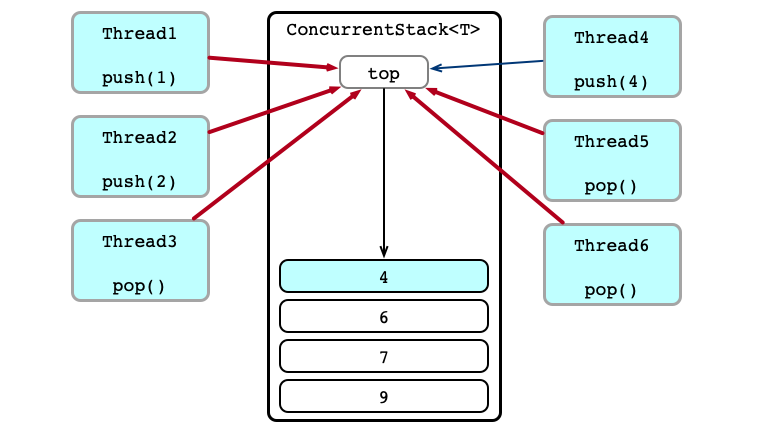
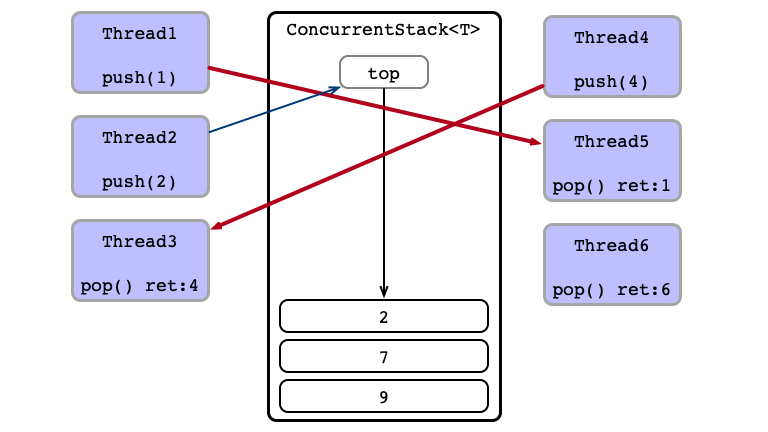
Contention!

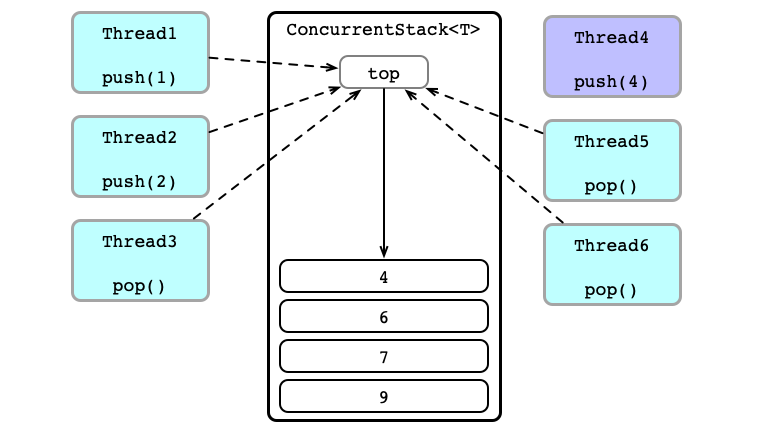
Thead 3 Wins

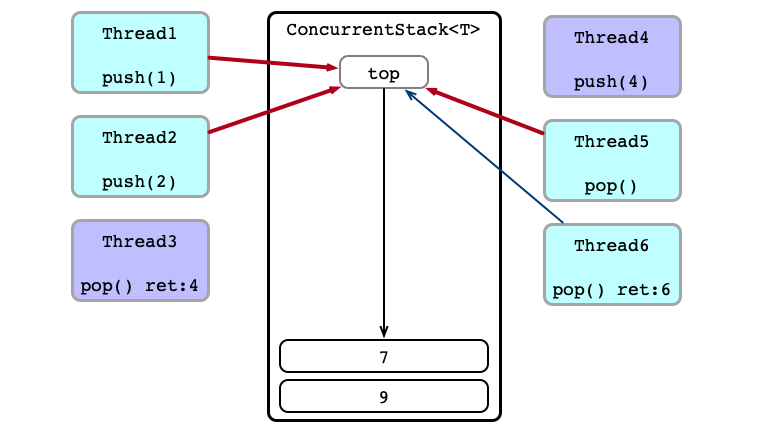
Contention!

Thead 6 Wins

Contention!

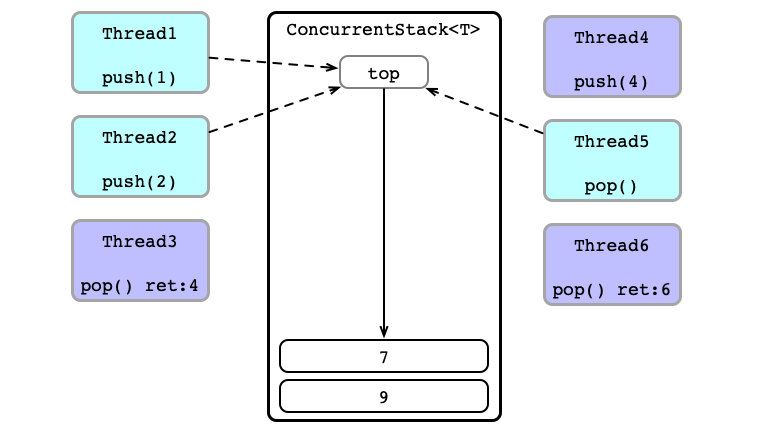
Thead 2 Wins

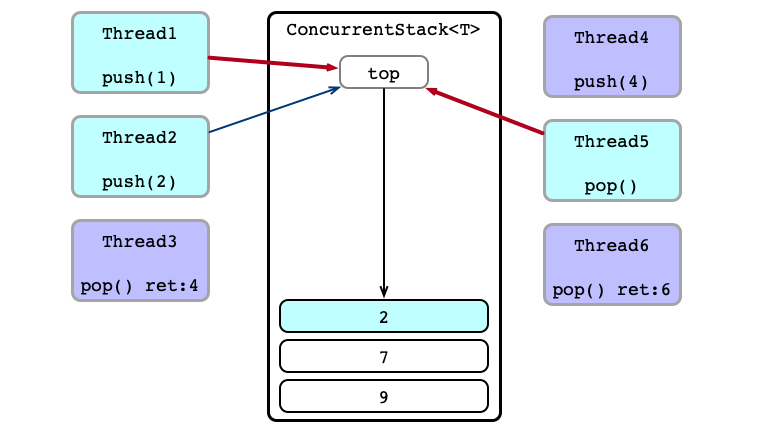
Contention!

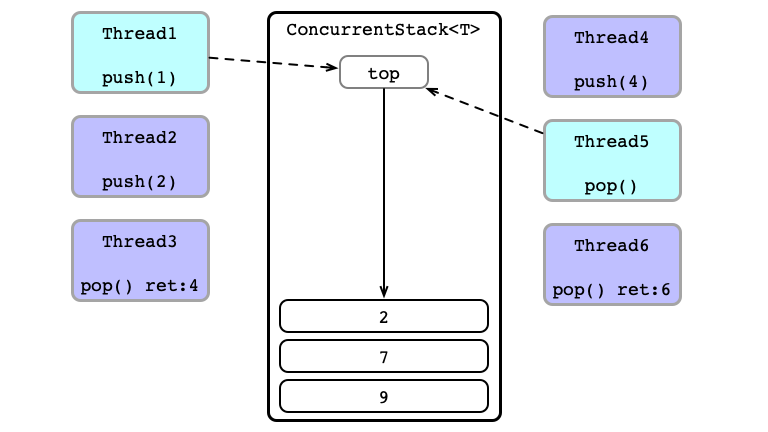
Thead 1 Wins

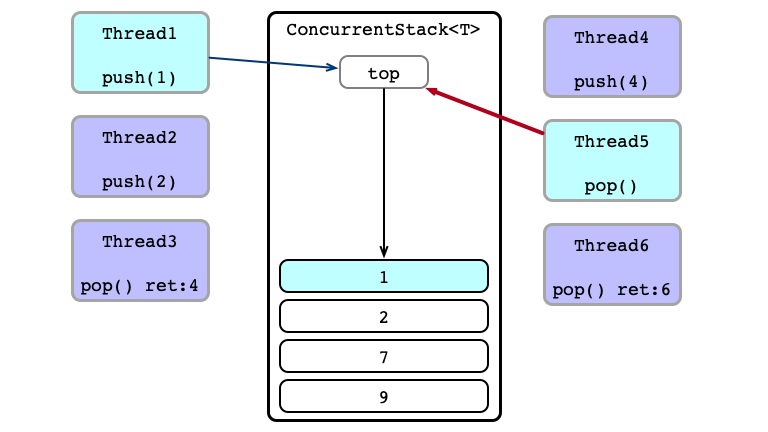
No Contention; Thread 5 Succeeds

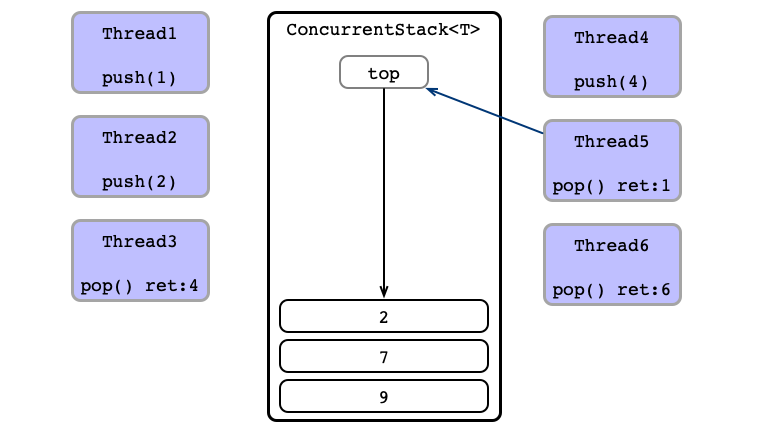
What do we need the stack for?

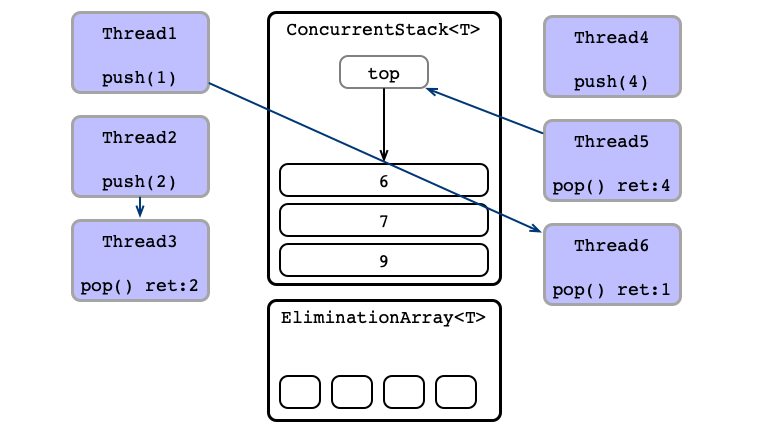
Equivalent Execution:

1. Thread 6 pops
2. Thread 1 sends 1 to Thread 5
3. Thread 4 sends 4 to Thread 3
4. Thread 2 pushes 2

Note: Steps 1, 2, and 3 can be performed in parallel!

Exchanges

Exchanges

Observation

• Stack operations cannot be parallelized
• Exchanges between threads can be!

The stack was just slowing us down

A Different Strategy

1. Attempt to push/pop to stack
   • if success, good job
2. If attempt fails there was contention; try to find a partner
   • if push, try to find a pop and give them your value
   • if pop, try to find a push and take their value

This strategy is called elimination

• eliminate unnecessary calls to push/pop

Need Another Object

The Exchanger object:

• Stores reference to item to be exchanged
• Has method exchange(T item,...)
  • ... parameters for timeout

Specification of Exchanger<T> ex:

• ThreadA calls ex.exchange(itemA,...)
• ThreadB calls ex.exchange(itemB,...)
• ThreadA receives itemB
• ThreadB receives itemA

Exchange Semantics

• Use ex.exchange(null,...) to indicate pop
• Use ex.exchange(item,...) to indicate push(item)

Exchange a success if:

• ThreadA calls ex.exchange(item)
  • call returns null (i.e., other call was a pop)
• ThreadB calls ex.exchange()
  • call returns item != null (i.e. other call was push(item))

Finding a Partner

Store an array of several Exchanger instances

1. Attempt to push/pop to stack
   • if success, good job
2. If attempt fails there was contention; try to find a partner
   • pick random Exchanger ex in array
   • call
     • ex.exchange(null) for pop()
     • ex.exchange(item) for push()
   • wait until success, or timeout
     • timeout $\implies$ back to step 1

Elimination Stack

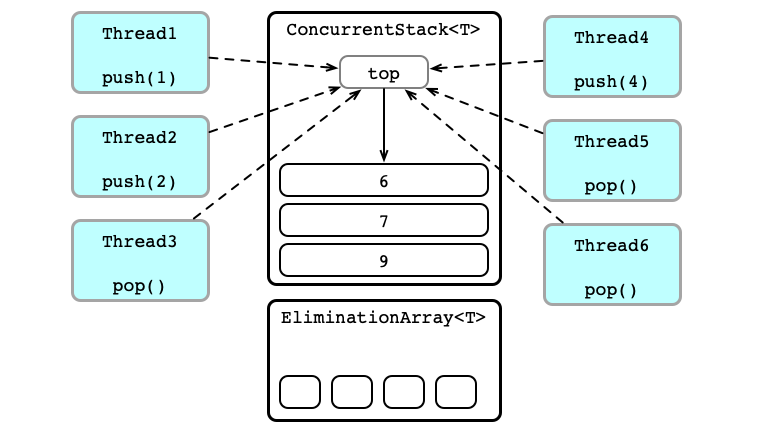
Witness Contention

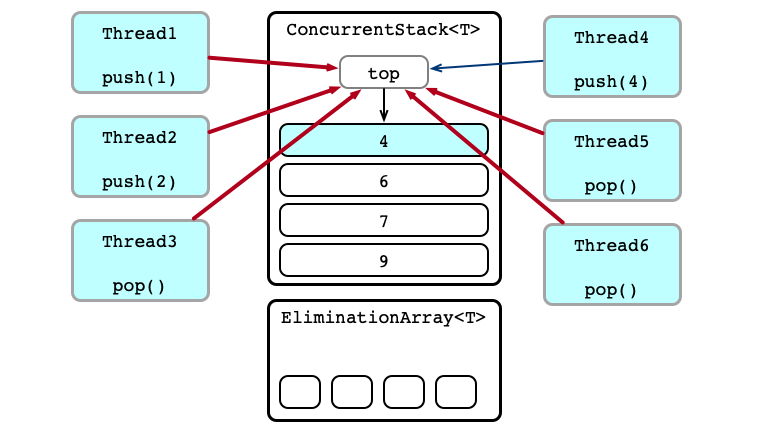
Attempt to Exchange

Some Exchanges Successful!

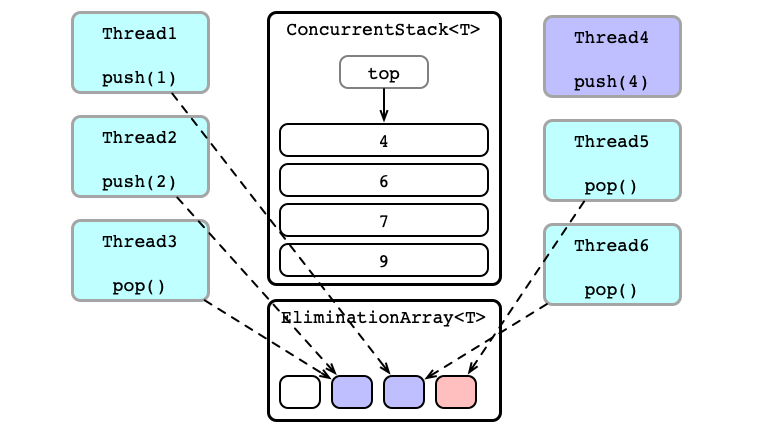
Unsuccessful Exchanges Try Again

Challenges

1. Implementation (see AoMP Section 11.4)
   • natural idea
   • technically challenging
2. Parameter tuning
   • how large should Exchanger array be?
   • dynamic tuning?
     • detect contention for exchangers, and use more?

Question. When might this approach be practical?

Consensus

Mission Critical Components

Suppose you’re designing an airplane

1. Need computers to control everything
   • sensors for speed, thrust, flap positions, pitch, roll, yaw
   • must adjust constantly to fly
2. But computers occassionally (regularly) crash/need restart

How to design around this issue?

Fault-Tolerance through Duplication?

Have multiple duplicate, independent systems

• systems run in parallel
• highly unlikely both crash simultaneously
  • restarts are infrequent
  • restarting one system won’t affect other system

The end of our worries?

Trouble Ahead

Suppose all systems working normally, but

• system 1 says increase thrust
• system 2 says decrease thrust
• system 3 not responding (restart?)

What do we do?

The Problem of Consensus

Have multiple systems with different inputs

• For us, binary inputs
  • 0 = decrease thrust
  • 1 = increase thrust

Goal:

• agree on same output

Requirements

Consensus Problem:

• Agreement: all systems output the same value
• Validity: if all systems have the same intput, they all output that value
• Termination: all (non-faulty) processes decide on an output and terminate after a finite number of steps

Coming up: How can we achieve consensus if some processes might fail?