Lecture 19: Pools and Queues
Overview
- Finishing Up Lists
- Pools & Queues
- A Blocking Queue
- A Lock-free Queue
Last Time: Lock-free linked list
Use AtomicMarkableReference<Node> for fields
-
markindicates logical removal
For add/remove:
- Find location
- Validate and modify
- (first logically remove if
remove) - use
compareAndSetto atomically- check that predecessor node has not been removed
- update
nextfield of predecessor
- (first logically remove if
For contains:
- Just traverse the list!
Common Functionality
Traverse are remove:
- Find
predandcurrwhereitemlives - Physically remove logically removed nodes along the way
Return: a Window
class Window {
public Node pred;
public Node curr;
public Window (Node pred, Node curr) {
this.pred = pred;
this.curr = curr;
}
}
Finding and Removing in Code
public Window find(Node head, long key) {
Node pred = null;
Node curr = null;
Node succ = null;
boolean[] marked = {false};
boolean snip;
retry: while(true) {
pred = head;
curr = pred.next.getReference();
while(true) {
succ = curr.next.get(marked);
while(marked[0]) {
snip = pred.next.compareAndSet(curr, succ, false, false);
if (!snip) continue retry;
curr = pred.next.getReference();
succ = curr.next.get(marked);
}
if (curr.key >= key) {
return new Window(pred, curr);
}
pred = curr;
curr = succ;
}
}
Removal in Code
public boolean remove(T item) {
int key = item.hashCode();
boolean snip;
while (true) {
Window window = find(head, key);
Node pred = window.pred;
Node curr = window.curr;
if (curr.key != key) {
return false;
}
Node succ = curr.next.getReference();
snip = curr.next.compareAndSet(succ, succ, false, true);
if (!snip) {
continue;
}
pred.next.compareAndSet(curr, succ, false, false);
return true;
}
}
Test the Code
Single Thread Performance
Runtimes: 1M Operations
| n elts | coarse | fine | optimistic | lazy | non-block |
|---|---|---|---|---|---|
| 10 | 0.11 s | 0.14 s | 0.13 s | 0.11 s | 0.11 s |
| 100 | 0.14 s | 0.46 s | 0.19 s | 0.13 s | 0.20 s |
| 1000 | 1.1 s | 3.9 s | 2.2 s | 1.1 s | 2.8 s |
| 10000 | 28 s | 39 s | 59 s | 29 s | 66 s |
Performance, 8 Threads
Runtimes: 1M Operations
| n elts | coarse | fine | optimistic | lazy | non-block |
|---|---|---|---|---|---|
| 10 | 0.21 s | 0.36 s | 0.33 s | 0.33 s | 0.21 s |
| 100 | 0.27 s | 1.80 s | 0.38 s | 0.12 s | 0.07 s |
| 1000 | 1.8 s | 4.7 s | 0.86 s | 0.19 s | 0.49 s |
| 10,000 | 32 s | 17 s | 9.2 s | 4.7 s | 9.2 s |
Note: fewer elements $\implies$ greater contention
The Moral
Many ways of achieving correct behavior
Tradeoffs:
- Conceptual simplicity vs complexity/sophistication
- Best performance depends on usage case
- very high contention: coarse locking is best
- simplest
- moderately high contention: non-blocking is best
- most sophisticated
- hardest to reason about
- easiest to mess up
- lower contention: lazy is best
- moderately sophisticated
- very high contention: coarse locking is best
More Data Structures
Recently:
- Thread pools to simplify thread/task management
Questions:
- What is a pool?
- How are they implemented?
A Pool<T> Interface
Want to model producer/consumer problem
- producers create things (e.g., tasks)
- consumers consume things (e.g., complete tasks)
A pool stores items between production and consumption:
public interface Pool<T> {
void put(T item); // add item to the pool
T get(); // remove item from pool
}
Pool Properties
- Bounded vs unbounded
- Fairness
- FIFO queue
- LIFO stack
- Something else?
- Method specifications
- partial: threads wait for conditions
-
getfrom empty pool waits for aput -
putto full pool waits for aget
-
- total: no calls wait for others
- synchronous: e.g. every
putcall waits forget
- partial: threads wait for conditions
Implementing a Pool
Can use a queue to implement a pool:
-
enqimplementsput -
deqimplementsget - LIFO priority
Two queue implementations today
- Unbounded total queue (blocking)
- Lock-free unbounded total queue
Unbounded Total Queue (Blocking)
- Use linked list implementation of queue
- Store:
-
Node headsentinal-
deqreturnshead.nextvalue (if any), updateshead
-
-
Node tail-
enqupdatestail.next, updatestail
-
-
- Locks:
-
enqLocklocksenqoperation -
deqLocklocksdeqoperation - individual
Nodes are not locked
-
Unbounded Queue in Pictures
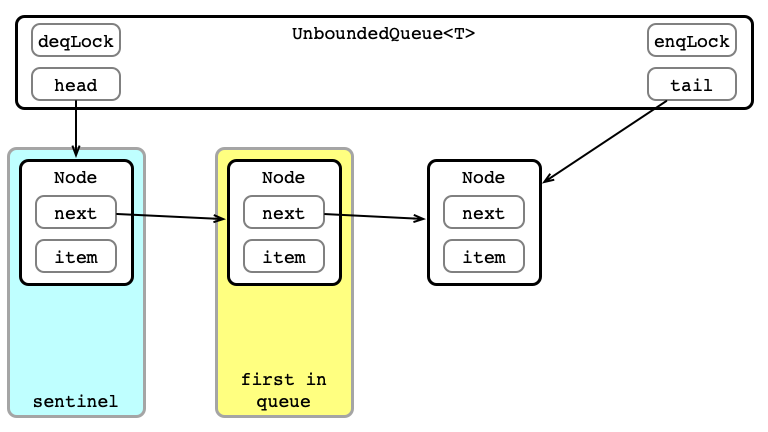
Dequeue 1: Aquire deqLock
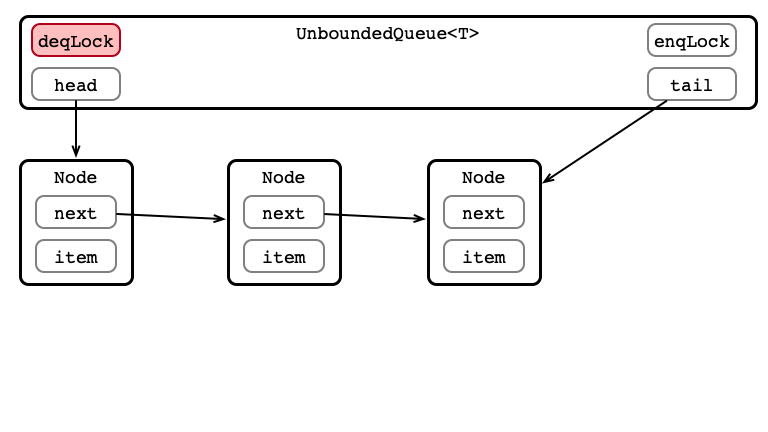
Dequeue 2: Get Element (or Exception)
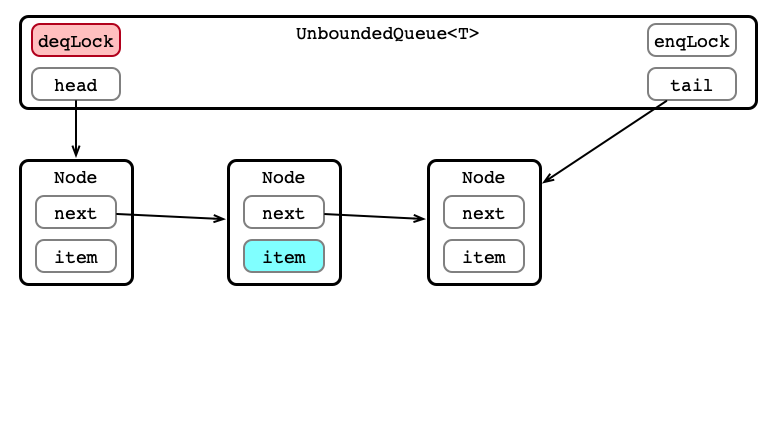
Dequeue 3: Update head
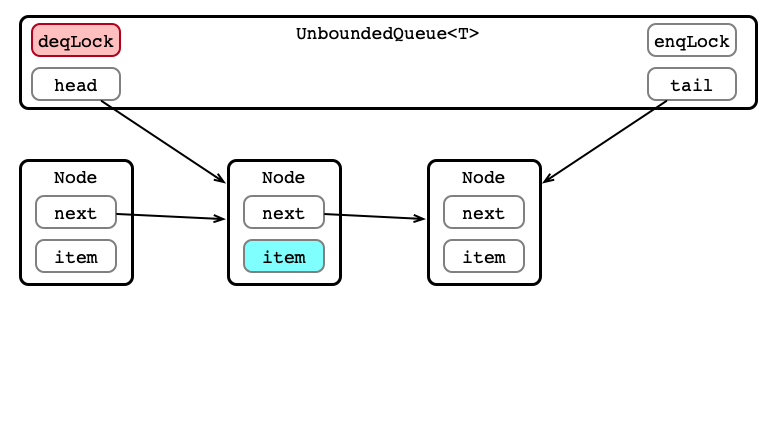
Dequeue 4: Release Lock
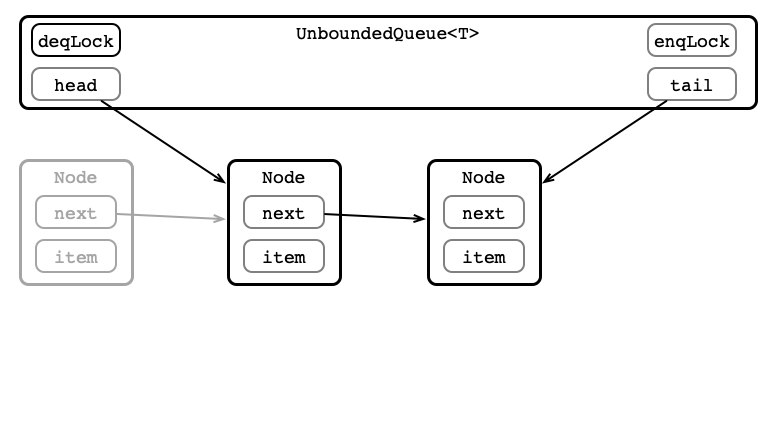
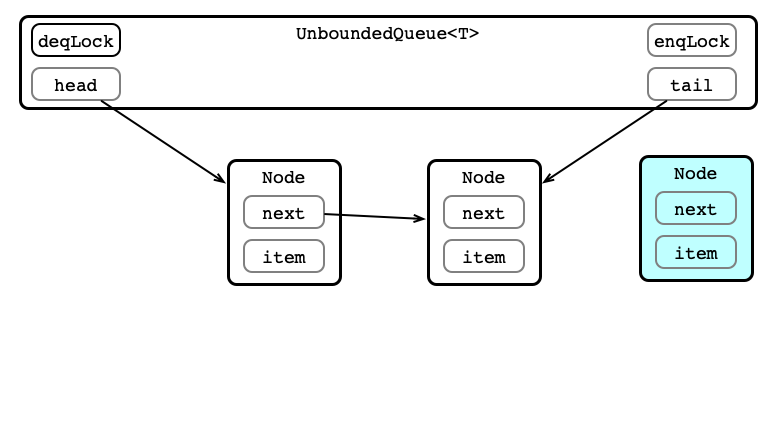
Enqueue 1: Make Node
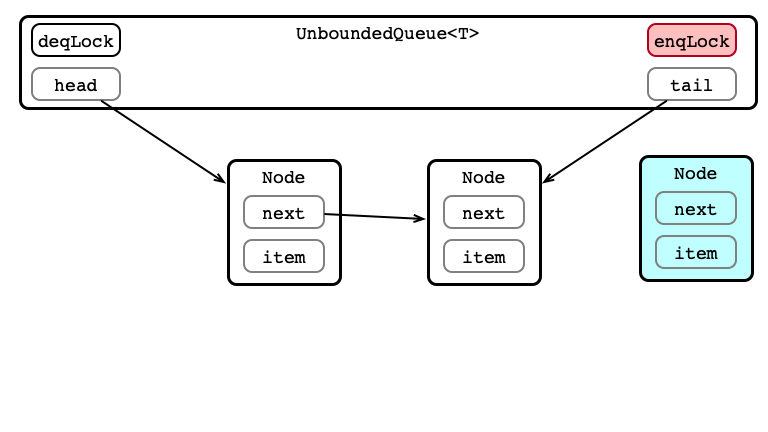
Enqueue 2: Acquire enqLock
Enqueue 3: Update tail.next
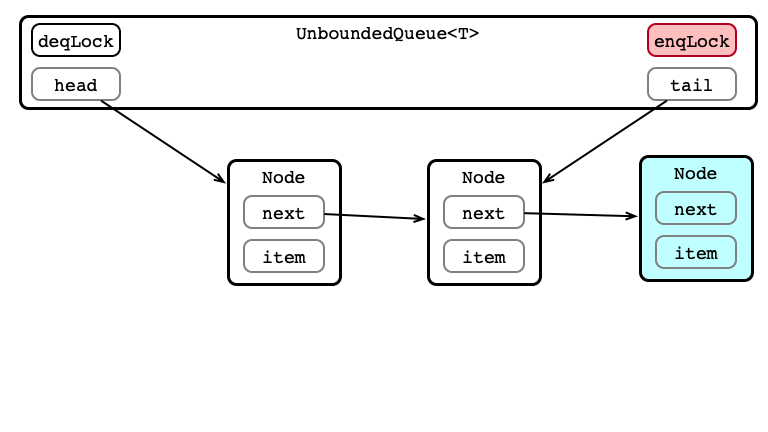
Enqueue 4: Update tail
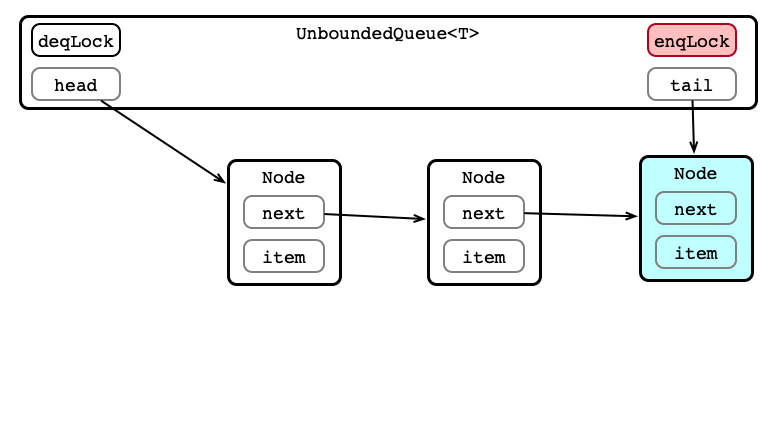
Enqueue 5: Release Lock
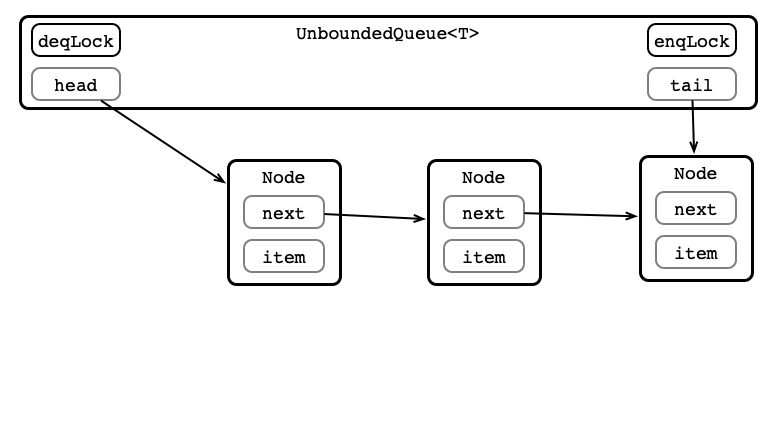
UnboundedQueue in Code
public class UnboundedQueue<T> implements SimpleQueue<T> {
final ReentrantLock enqLock;
final ReentrantLock deqLock;
volatile Node head;
volatile Node tail;
public UnboundedQueue() {
head = new Node(null);
tail = head;
enqLock = new ReentrantLock();
deqLock = new ReentrantLock();
}
public T deq() throws EmptyException {
T value;
deqLock.lock();
try {
if (head.next == null) {
throw new EmptyException();
}
value = head.next.value;
head = head.next;
} finally {
deqLock.unlock();
}
return value;
}
public void enq (T value) {
enqLock.lock();
try {
Node nd = new Node(value);
tail.next = nd;
tail = nd;
} finally {
enqLock.unlock();
}
}
class Node {
final T value;
volatile Node next;
public Node (T value) {
this.value = value;
}
}
}
Unbounded Logic
Easy to reason about:
- concurrent calls to
enq- one acquires
enqLock - others wait
- one acquires
- concurrent calls to
deq- one acquires
deqLock - others wait
- one acquires
What about concurrent calls to enq/deq?
- Ever an issue?