Lecture 18: Lazy and Nonblocking Lists
Overview
- Logical Removal and Lazy Lists
- Nonblocking Lists
- List Appraisal
Last Time(s)
- Coarse-grained synchronization
- lock the whole data structure for each operation
- Fine-grained synchronization
- lock the parts of the data structure currently being accessed
- Optimistic synchronization
- don’t lock until ready to modify
- validate between locking and modification
- validation failure $\implies$ restart
Optimistic Insertion
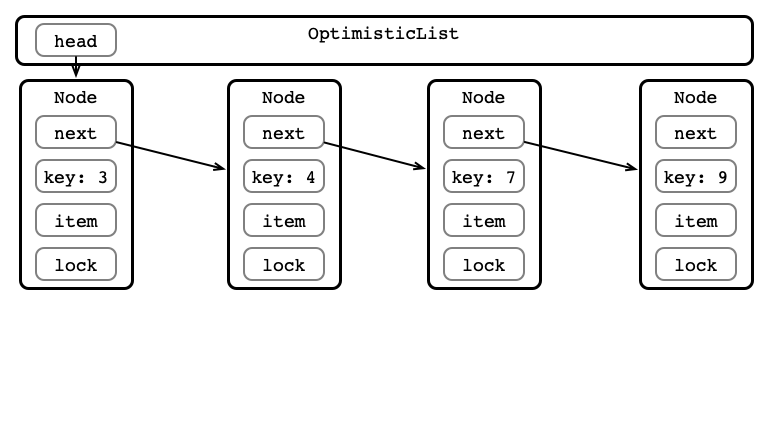
Step 1: Traverse the List
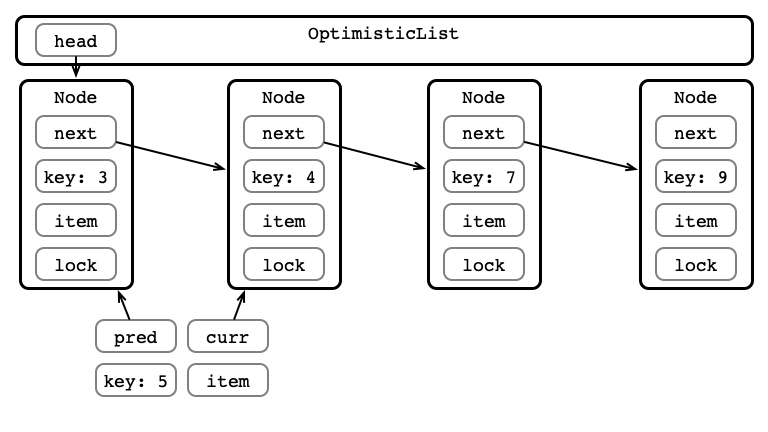
Step 1: Traverse the List
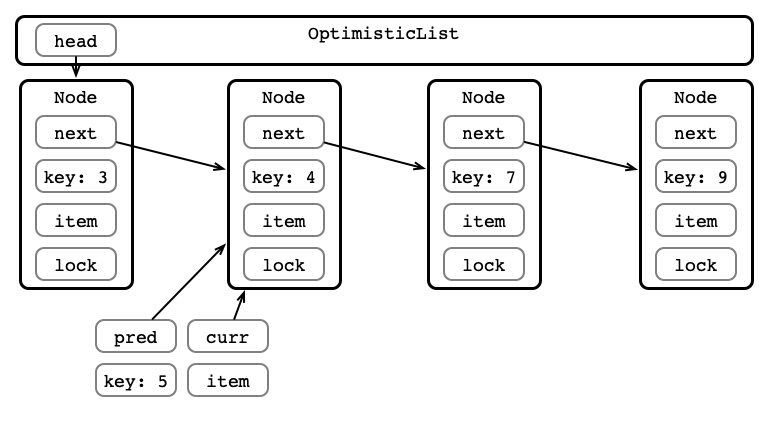
Step 1: Traverse the List
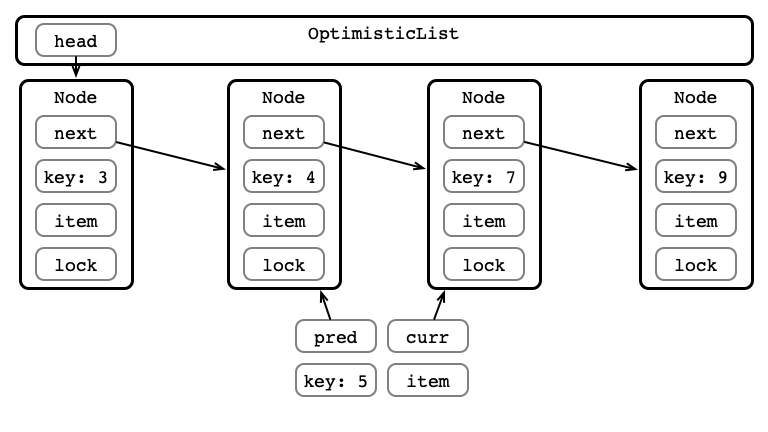
Step 2: Acquire Locks
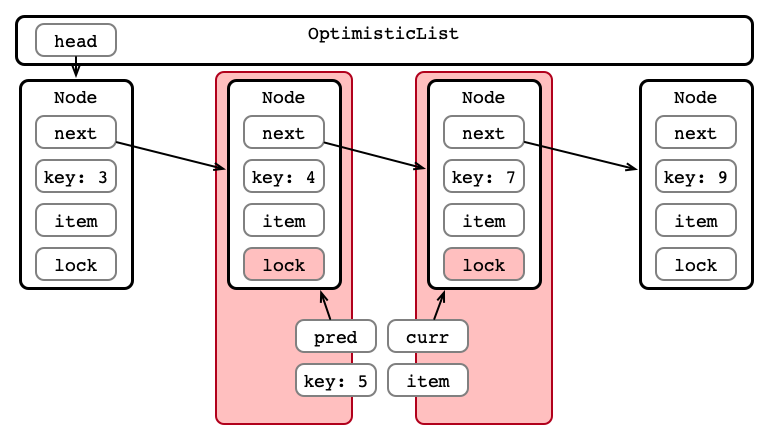
Step 3: Validate List - Traverse
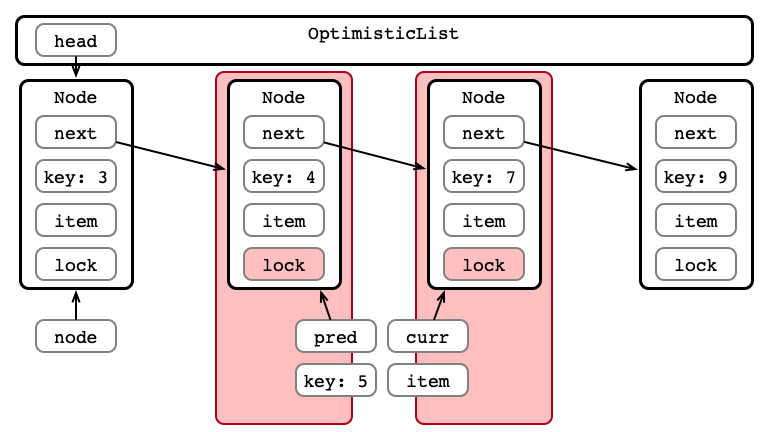
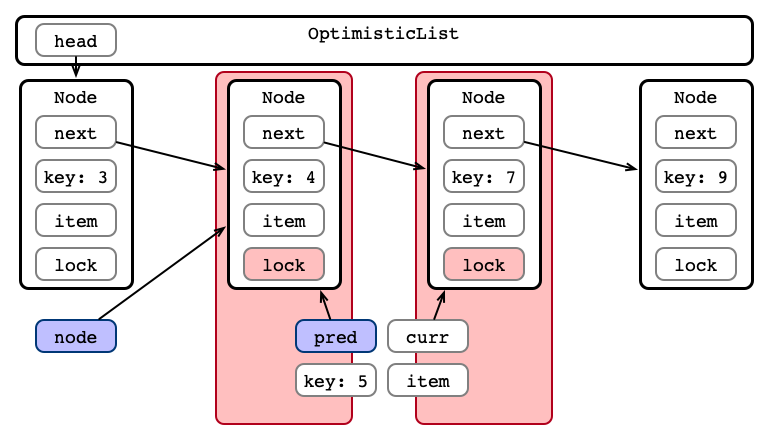
Step 3: Validate List - pred Reachable?
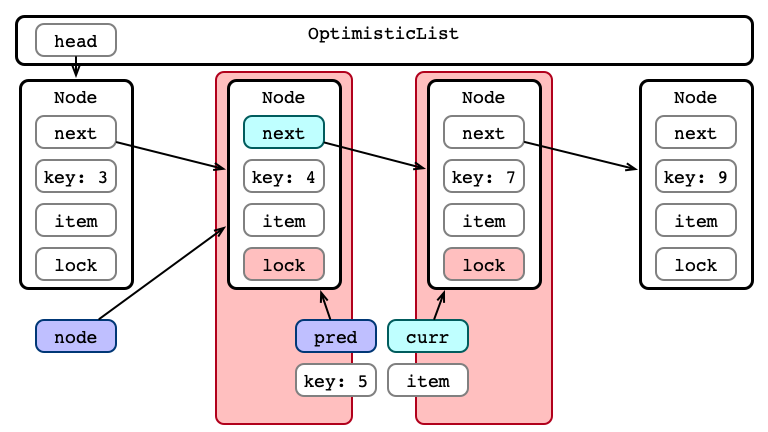
Step 3: Validate List - Is curr next?
Step 4: Perform Insertion
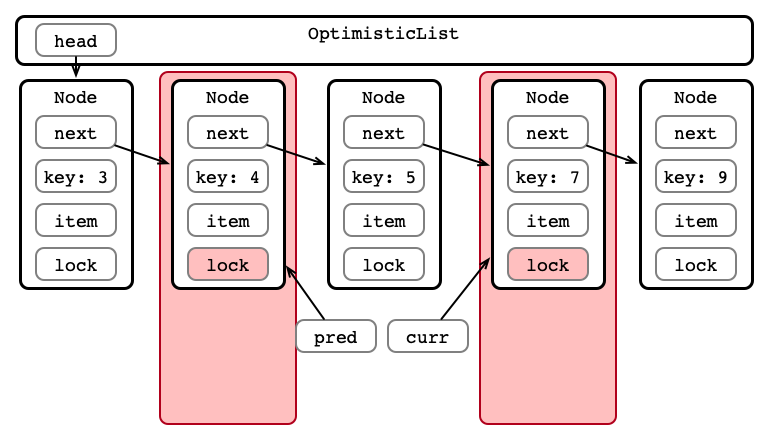
Step 5: Release Locks
Performance, Single Threaded
Runtimes: 1M Operations
| num elements | coarse-grained | fine-grained | optimistic |
|---|---|---|---|
| 10 | 0.11 s | 0.14 s | 0.13 s |
| 100 | 0.14 s | 0.46 s | 0.19 s |
| 1000 | 1.1 s | 3.9 s | 2.2 s |
| 10000 | 28 s | 39 s | 59 s |
- fine-grained slow-down: more locks
- optimistic slow-down: validataion
Performance, 8 Threads
Runtimes: 1M Operations
| num elements | coarse-grained | fine-grained | optimistic |
|---|---|---|---|
| 10 | 0.21 s | 0.36 s | 0.33 s |
| 100 | 0.27 s | 1.80 s | 0.38 s |
| 1000 | 1.8 s | 4.7 s | 0.86 s |
| 10,000 | 32 s | 17 s | 9.2 s |
Note: fewer elements $\implies$ greater contention
Optimism and Validation
Under best circumstances:
- validation succeeds
- likely if little contention
- still traverse the list twice
Under contention:
- all operations are blocking
- not wait-free
- contention can lead to validation failures
- not starvation-free
Observation
Operations are complicated because they consist of several steps
- hard to reason about when the operation appears to take place
- coarse/fine-grained synchronization stop other threads from seeing operations “in progress”
- optimistic synchronization may encounter “in progress” operations before locking
- validation required
Lazy Synchronization
-
Mark a node before physical removal
- marked nodes are logically removed, still physically present
- Only marked nodes are ever removed
Validation simplified:
- Just check if nodes are marked
- No need to traverse whole list!
Lazy Operation
- Traverse without locking
- Lock relevant nodes
- Validate list
- check nodes are
- not marked
- correct relationship
- if validation fails, go back to Step 1
- check nodes are
- Perform operation
- for removal, mark node first
- Unlock nodes
Lazy Removal Illustrated
Step 1: Traverse List
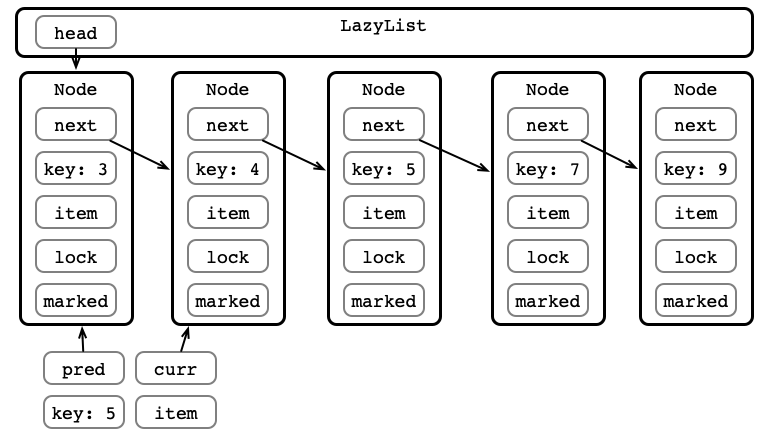
Step 1: Traverse List
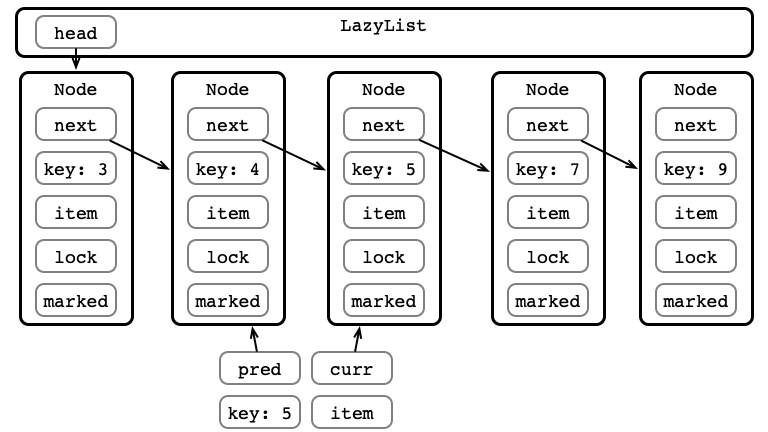
Step 2: Lock Nodes
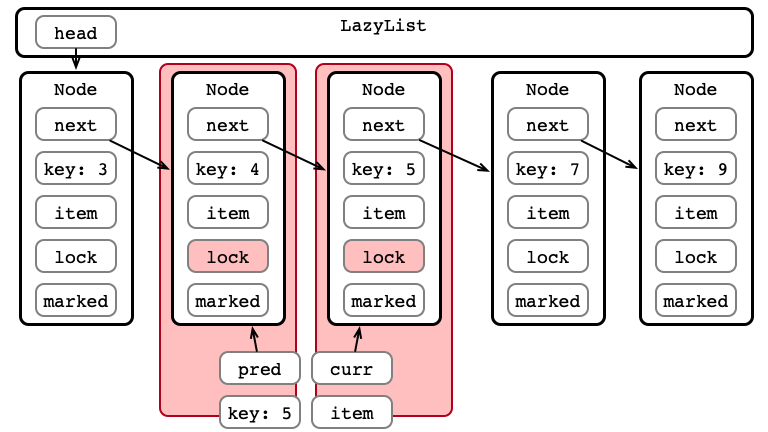
Step 3: Validate pred.next == curr?
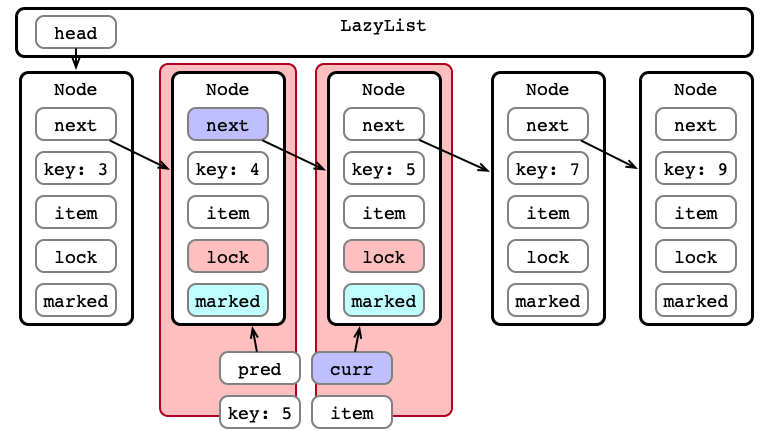
Step 3: Validate not marked?

Step 4a: Perform Logical Removal
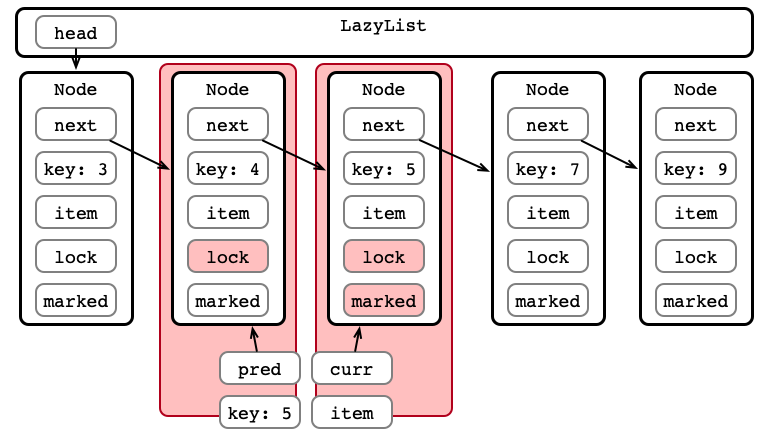
Step 4b: Perform Physical Removal
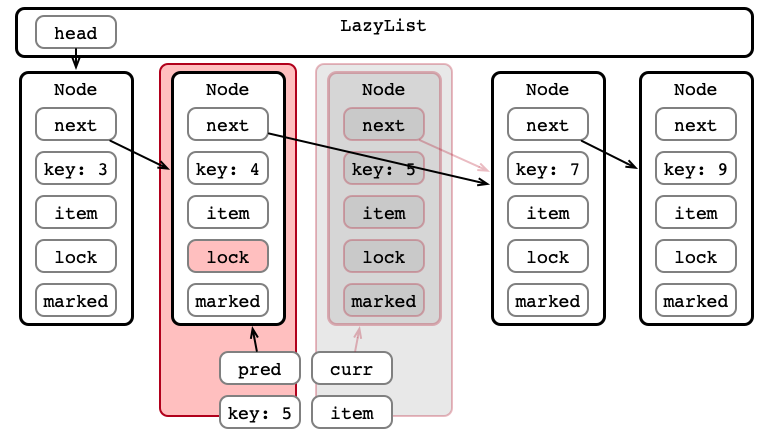
Step 5: Release Locks and Done!
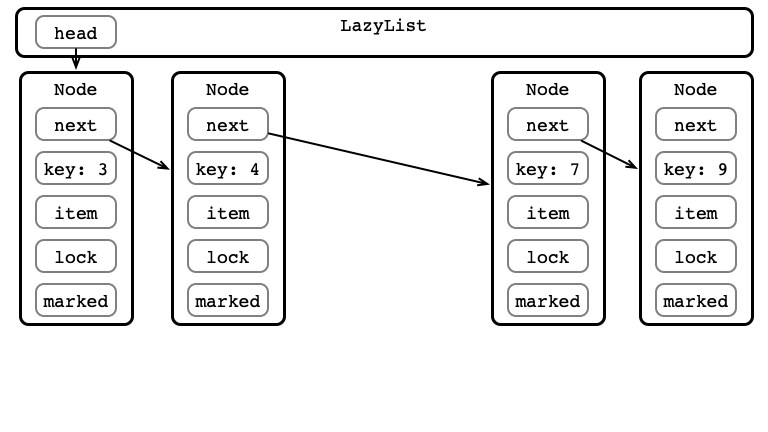
A Node in Code
private class Node {
T item;
int key;
Node next;
Lock lock;
volatile boolean marked;
public Node (int key) {
this.item = null;
this.key = key;
this.next = null;
this.lock = new ReentrantLock();
this.marked = false;
}
public Node (T item) {
this.item = item;
this.key = item.hashCode();
this.next = null;
this.lock = new ReentrantLock();
}
public void lock () {
lock.lock();
}
public void unlock () {
lock.unlock();
}
}
Validation, Simplified
private boolean validate (Node pred, Node curr) {
return !pred.marked && !curr.marked && pred.next == curr;
}
Improvements?
- Limited locking as in optimistic synchronization
- Simpler validation
- faster—no list traversal
- more likely to succeed?
- Logical removal easier to reason about
- linearization point at logical removal line
-
contains()no longer acquires locks- often most frequent operation
- now it is wait-free!
Wait-free Containment
public boolean contains (T item) {
int key = item.hashCode();
Node curr = head;
while (curr.key < key) {
curr = curr.next;
}
return curr.key == key && !curr.marked;
}
Testing Performance!
Single Thread Performance
Runtimes: 1M Operations
| n elts | coarse | fine | optimistic | lazy |
|---|---|---|---|---|
| 10 | 0.11 s | 0.14 s | 0.13 s | 0.11 s |
| 100 | 0.14 s | 0.46 s | 0.19 s | 0.13 s |
| 1000 | 1.1 s | 3.9 s | 2.2 s | 1.1 s |
| 10000 | 28 s | 39 s | 59 s | 29 s |
Performance, 8 Threads
Runtimes: 1M Operations
| n elts | coarse | fine | optimistic | lazy |
|---|---|---|---|---|
| 10 | 0.21 s | 0.36 s | 0.33 s | 0.33 s |
| 100 | 0.27 s | 1.80 s | 0.38 s | 0.12 s |
| 1000 | 1.8 s | 4.7 s | 0.86 s | 0.19 s |
| 10,000 | 32 s | 17 s | 9.2 s | 4.7 s |
Note: fewer elements $\implies$ greater contention
Lazy Appraisal
Advantages:
- Less locking than fine-grained
- More opportunities for parallelism than coarse-grained
- Simpler validataion than optimistic
- Wait-free
containsmethod
Disadvantages:
- Validation could still fail (though maybe less likely)
- Not starvation-free
- even if locks are starvation-free
-
addandremovestill blocking
What’s Next?
Can we make all of the operations wait-free?
- A concurrent list without locks?
Why Does LazyList Need Locks?
- Traverse without locking
- Lock relevant nodes
- Validate list
- Perform operation
- Unlock nodes
Why Does LazyList Need Locks?
The issue:
- Validation and modification are separate steps
- Must enforce that nodes are unchanged between validation and mod
Cause for hope:
- Validataion is simple, local:
private boolean validate (Node pred, Node curr) { return !pred.marked && !curr.marked && pred.next == curr; } - Modification (e.g.,
add) is simple, local:Node node = new Node(item); node.next = curr; pred.next = node; // this is the only step that modifies list!
An Idea
If we can
- combine validation and modification steps
- perform this operation atomically
then maybe we can avoid locking?
A Tool
Better living with atomics!
AtomicMarkableReference<T>- Stores
- a reference to a
T - a boolean
marked
- a reference to a
- Atomic operations
boolean compareAndSet(T expectedRef, T newRef, boolean expectedMark, boolean newMark)T get(boolean[] marked)T getReference()boolean isMarked()
An Algorithm?
Use AtomicMarkableReference<Node> for fields
-
markindicates logical removal
For add/remove:
- Find location
- Validate and modify
- (first logically remove if
remove) - use
compareAndSetto atomically- check that predecessor node has not been removed
- update
nextfield of predecessor
- (first logically remove if
For contains:
- Just traverse the list!
Next Week
Other linear data structures!
- Queues
- Stacks