Lecture 09: Linearizability and Progress
Last Time
- Sequential consistency:
- consistent with program order
- consistent with sequential specification
- Properties of sequential consistency
- not compositional
- sequentially consistent components do not imply sequential consistency
- nonblocking
- methods can give SC response without waiting for other pending method calls
- not compositional
Today
Linearizable objects and executions
Weird Thing about SC
SC makes no reference to invocation/response intervals for method calls
- Why bother with time intervals if we ignore them (execept relative order for single threads)?
Another idea
- Make sure execution is consistent with timing of method calls
- Consider sequential executions consistent with each method call taking effect at some instant during the method call
Same Example, Fewer Options
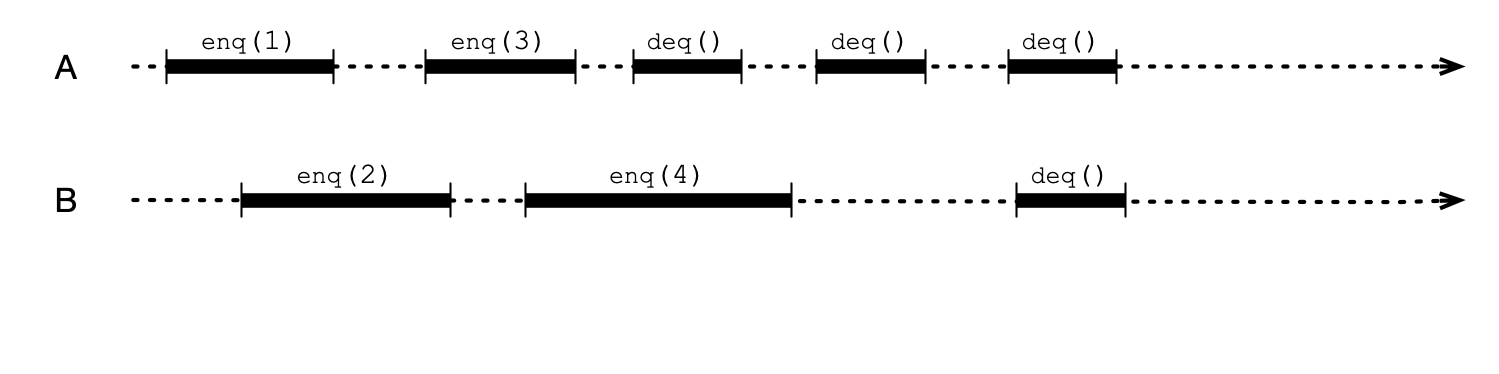
Can only change relative order of method calls if they overlap
Linearization Points
A linearization point is a point in a method call where method “takes effect”
- all events after linearization point see effect of method call
- linearization points must be distinct (correspond to some atomic operation)
Example of Linearization Points
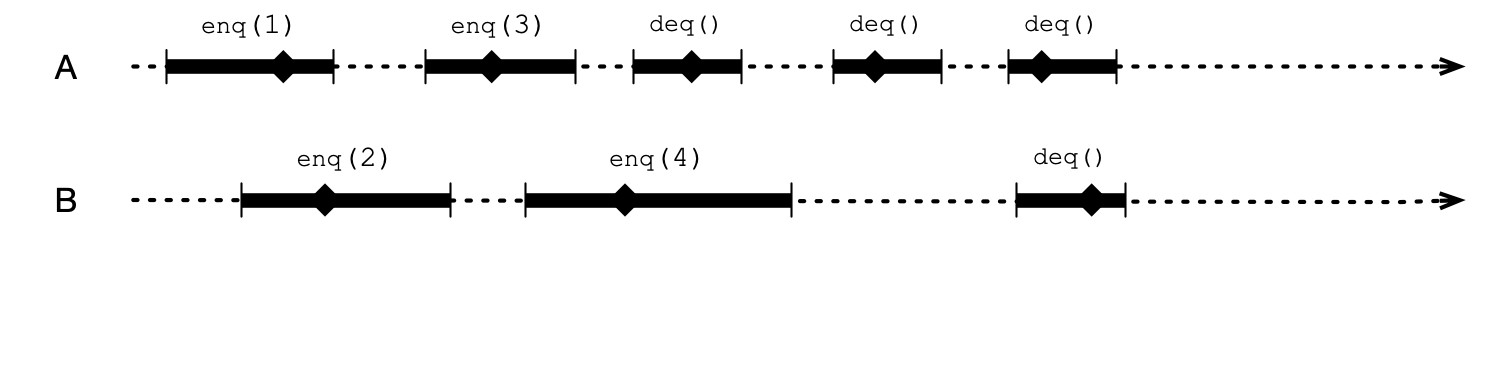
Equivalent Sequential Execution
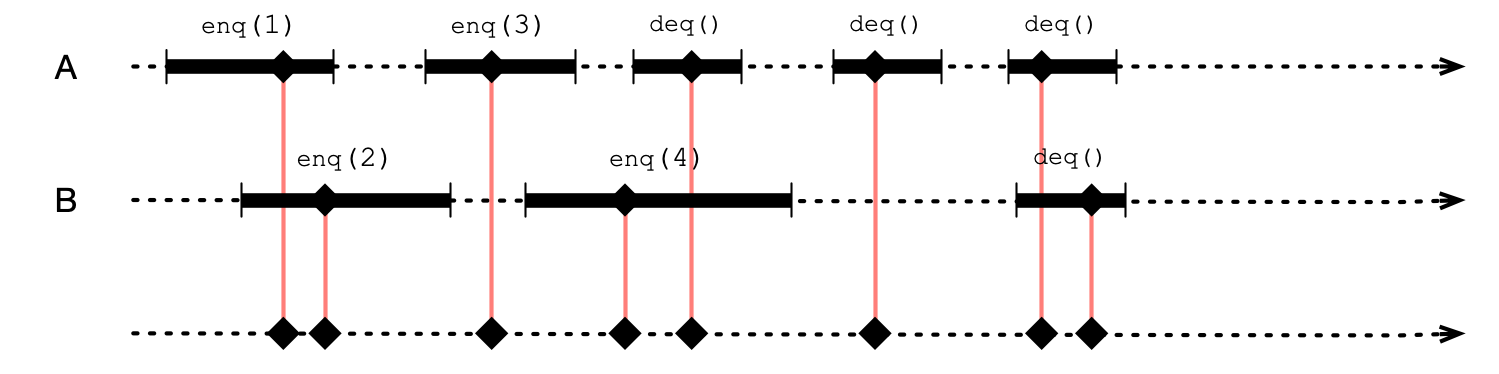
An Alternative Sequential Execution
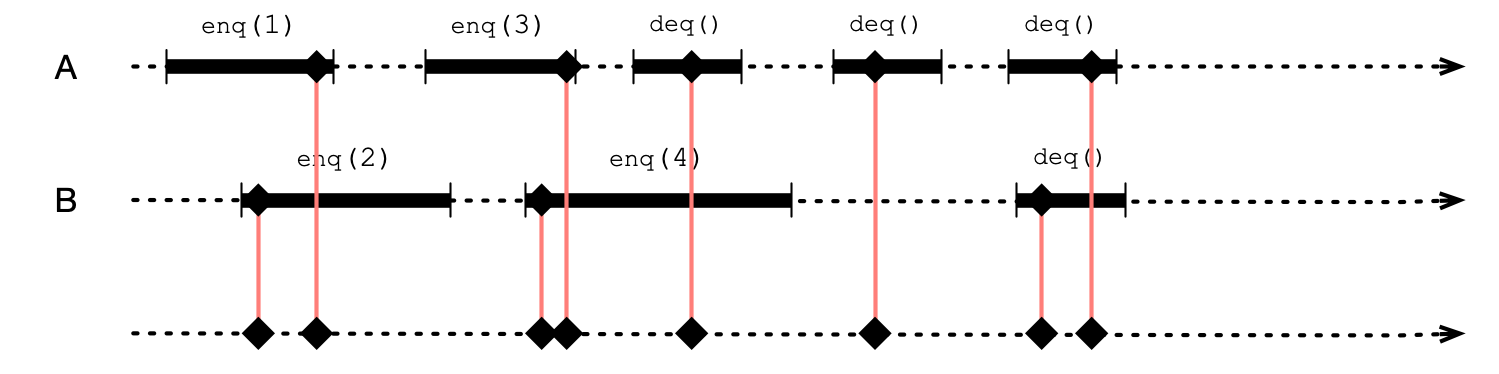
Linearizability
A concurrent execution is linearizable if:
- exists a linearization point in each method call such that execution is consistent with sequential execution where method calls occur in order of corresponding linearization points
An implementation of an object is linearizable if:
- it guarantees every execution is linearizable
Comparing Linearizability and SC
- Does linearizability imply sequential consistency?
- Does sequential consistency imply linearizability?
Linearizability $\implies$ SC
Must show:
- Maintains program order
- Satisfies sequential specification
SC $\nRightarrow$ Linearizability
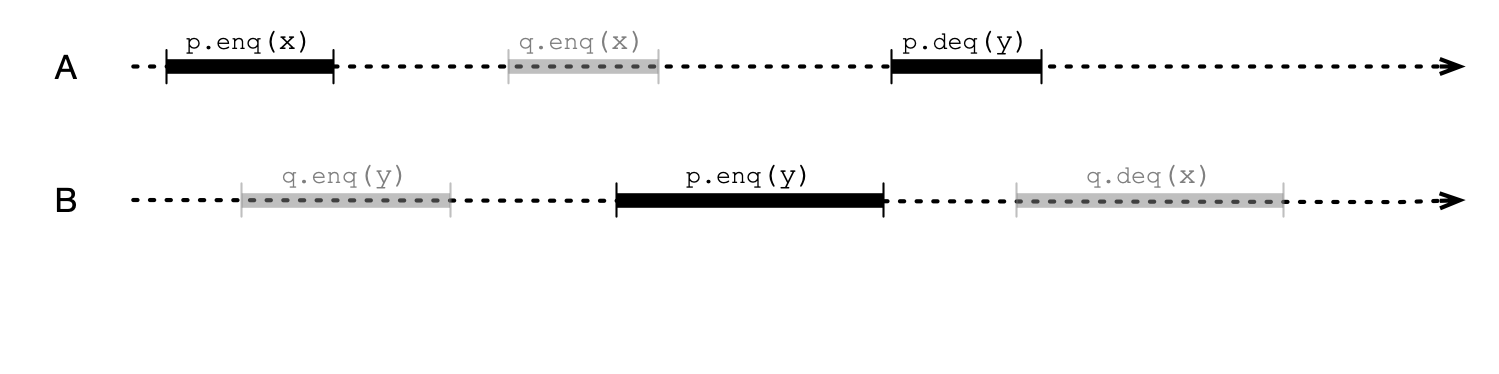
Compositionality
Recall this execution with 2 queues (not sequentially consistent)
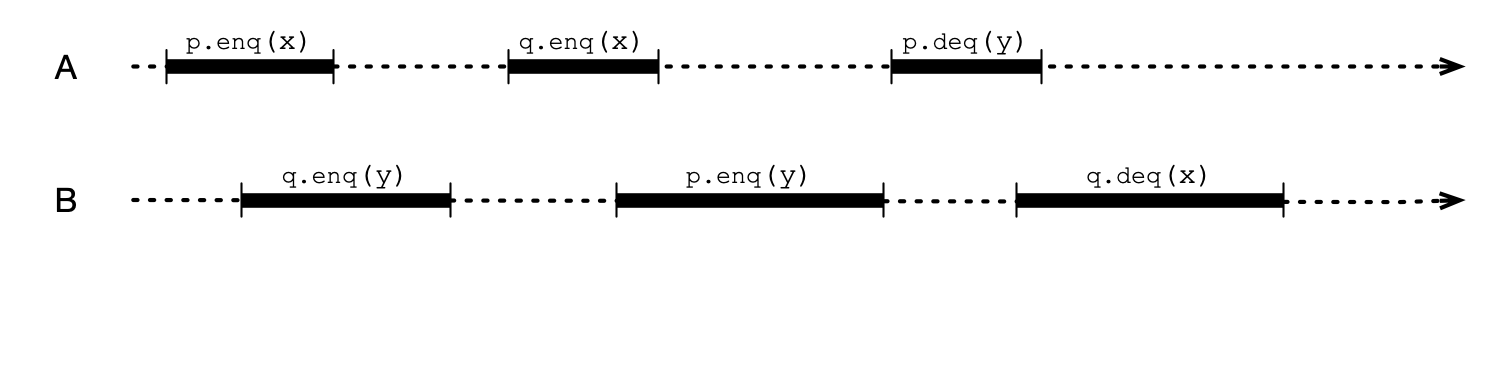
But…
p and q are not linearizable in this execution!

Two More Questions
- Are linearizable objects compositional?
- Is linearizability a nonblocking condition?
Are Linearizable Objects Compositional?
Is linearizability a nonblocking condition?
Coming Up
Implementations!
- locks
- data structures
Homework Questions
Question 1
Suppose \(n\) threads call the visit() method of a Bouncer object. Argue that the following hold:
- At most one thread gets the value
STOP. - At most \(n - 1\) threads get the value
DOWN. - At most \(n - 1\) threads get the value
RIGHT.
Question 2
Consider a 2D triangular array of Bouncer objects arranged as follows:
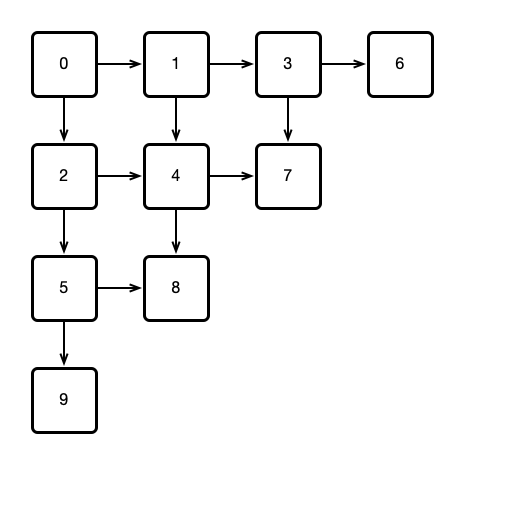
Question 2, Continued
Suppose:
- All threads start by calling
visit()onBouncer0. - Whenever a thread visits a
Bouncer, if theBouncerreturnsSTOP, the thread adopts the number of theBounceras its ID. - If
DOWNis returned, the thread then visits theBouncerbelow; ifRIGHTis returned, the thread visits theBouncerto the right.
- Show that for a sufficiently large array of
Bouncers, every thread will eventuallySTOPat someBouncer, thereby adopting its ID. - If the number \(n\) of threads is known in advance, how many
Bouncers are required to ensure that all threads adopt an ID?