Lecture 08: Concurrent Objects 3
Outline
- Sequential Consistency
- Linearizability
- Progress Conditions
Last Time
What is “correct” behavior for a concurrent execution of a data structure?
Sequential Consistency
Two Natual Desiderata
Method calls/responses consistent with some sequential execution
Method calls can be ordered such that:
-
they are consistent with program order
- if a single thread calls
methodOne()beforemethodTwo(), thenmethodOne()$\to$methodTwo()in sequential execution
- if a single thread calls
-
pre/post conditions for each method call satisfy data structure’s sequential specification
Such executions are sequentially consistent
Definition
An execution is sequentially consistent if all method calls can be ordered such that:
- they are consistent with program order
- they meet object’s sequential specification
An implementation of an object is sequentially consistent if it guarantees every execution is sequentially consistent
Example
What are possible outcomes of deq() calls in a sequentially consistent execution?
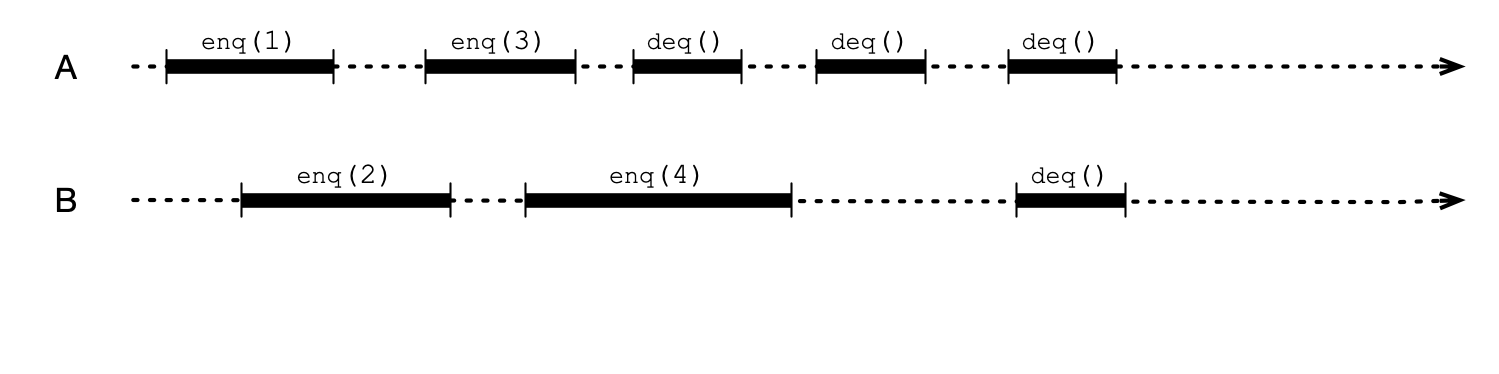
Sequential Consistency is Weak
- Method calls can appear interleaved in any order that maintains program order
- No guarantees for “real time” order
- (partially) order methods w.r.t. real time

Sequential Consistency is Nonblocking
Consider concurrent execution:
- Pending method call (invoked, but no response yet)
- Then: exists a response that can be made immediately that does not violate SC
It is possible to achieve SC without needing to wait for response from other pending methods
- May still be difficult to figure out which response will give SC execution
Nonblocking Example
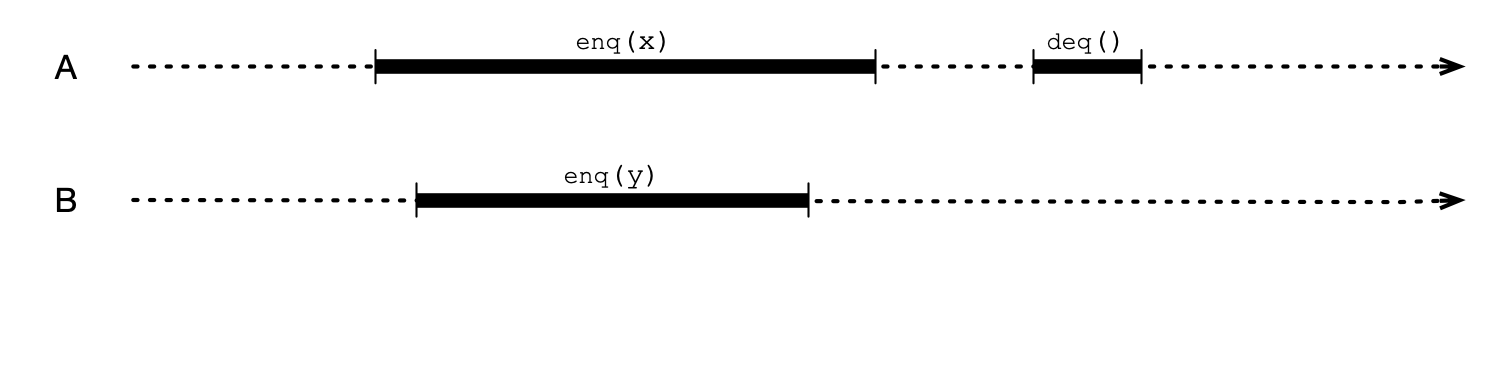
A Subtler Issue
Suppose we have a program two queues, p and q
- Implementation of queue guarantees sequentially consistency
Must an execution of a program with p and q be sequentially consistent?
An Execution
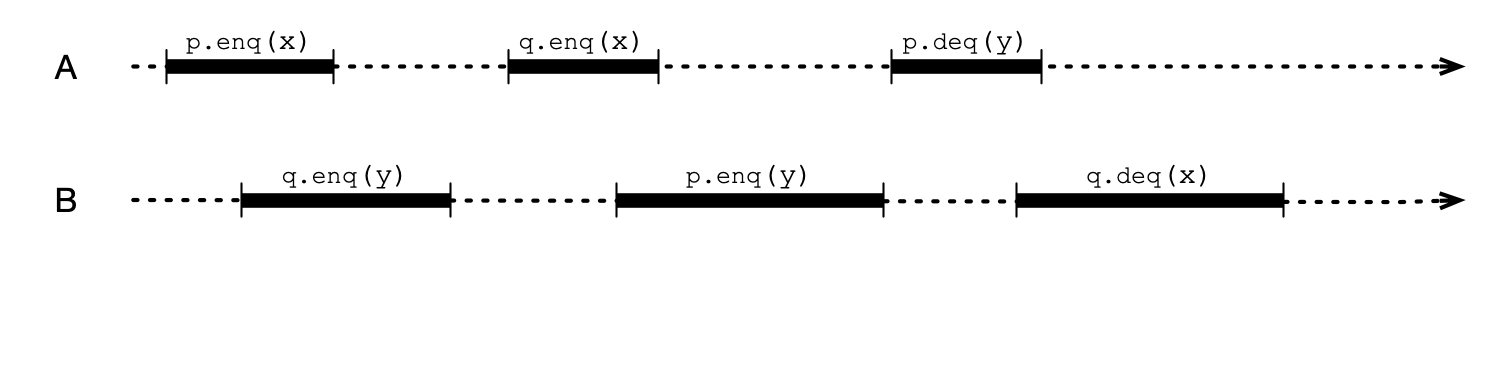
Sequentially Consistent for p
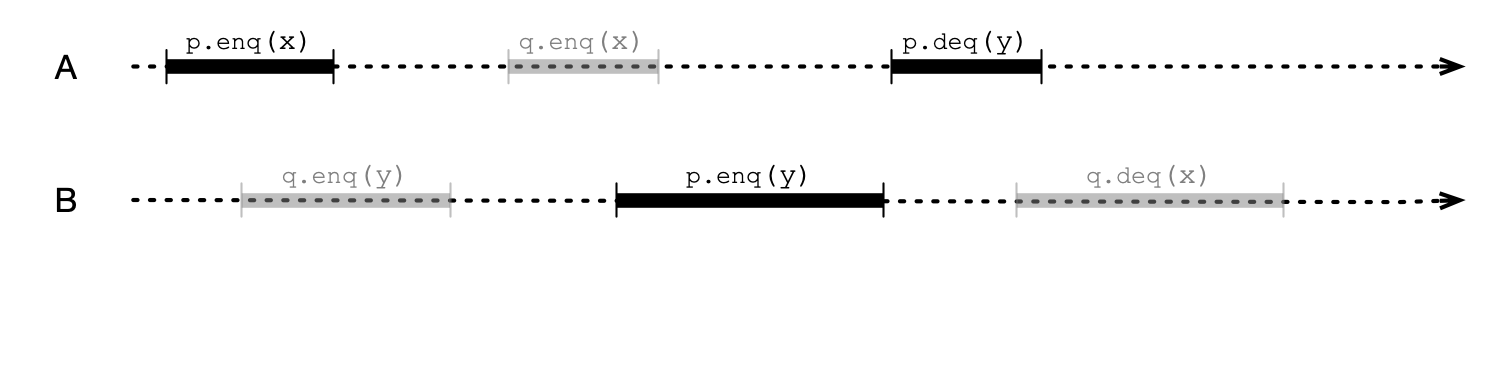
Sequentially Consistent for q
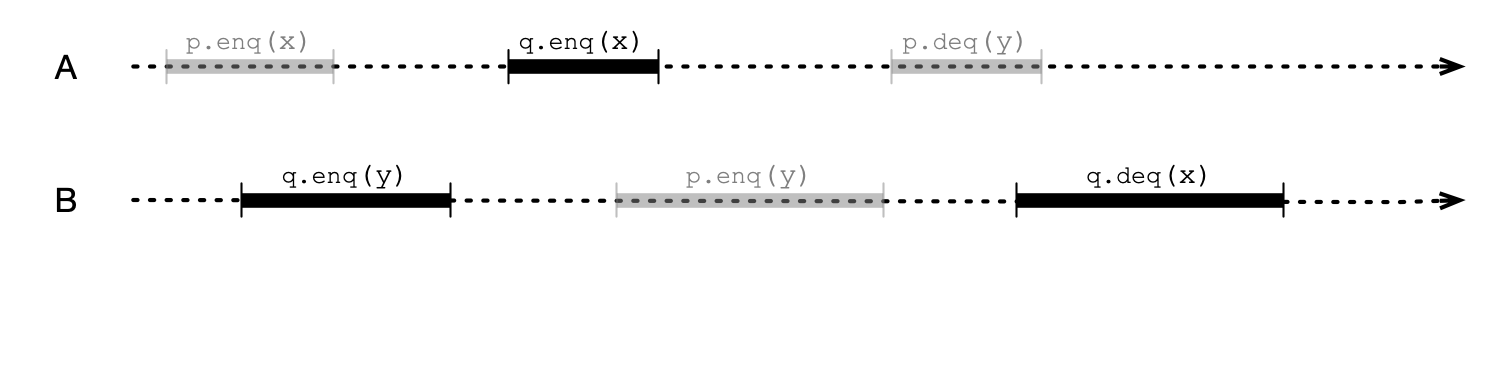
But is Execution SC?

Sequential Consistency is not Compositional
A property $\mathcal{P}$ is compositional if
- Whenever all objects in system satisfy $\mathcal{P}$, then system satisfies $\mathcal{P}$
Previous example shows:
- Sequential consistency is not compositional
Sequential Consistency Is…
- …Maybe the weakest reasonble guarantee we could expect of a concurrent implementation of an object
- …Potentially allows for a lot of parallelism
- SC is a nonblocking property
- …Not compositional
- a system made of SC components need not be SC!