Lab Week 12: Sorting Networks

Outline

1. Simple Sorting Algorithms
2. Sorting Networks
3. Sorting Activity

Last Time

Sorting by Divide and Conquer

• Merge sort
  1. sort left half
  2. sort left half
  3. merge sorted halves
• Quicksort
  1. pick pivot
  2. split according to pivot
     • left half less than pivot
     • right half at least pivot
  3. sort left half
  4. sort right half

Sorting Networks

Another view of sorting in parallel

Insertion Sort, Revisited

for (int i = 1; i < data.length; ++i) {
    for (int j = i; j > 0; --j) {
        if (data[j-1] > data[j]) {
            swap(data, j-1, j)		
        }
    }
}

Appealing Features of Insertion Sort

for (int i = 1; i < data.length; ++i) {
    for (int j = i; j > 0; --j) {
        if (data[j-1] > data[j]) {
            swap(data, j-1, j)		
        }
    }
}

1. Only modifications are (adjacent) swaps
   • sorting is in place
2. Access pattern is independent of input
   • inputs always read/compared in same order
   • only difference between execution is outcomes of swaps

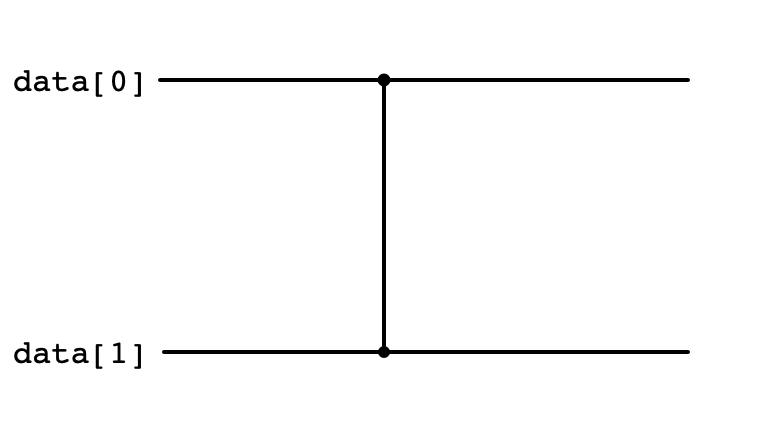
Comparators: Visualizing Swaps

        if (data[i] > data[j]) {
            swap(data, i, j)
        }

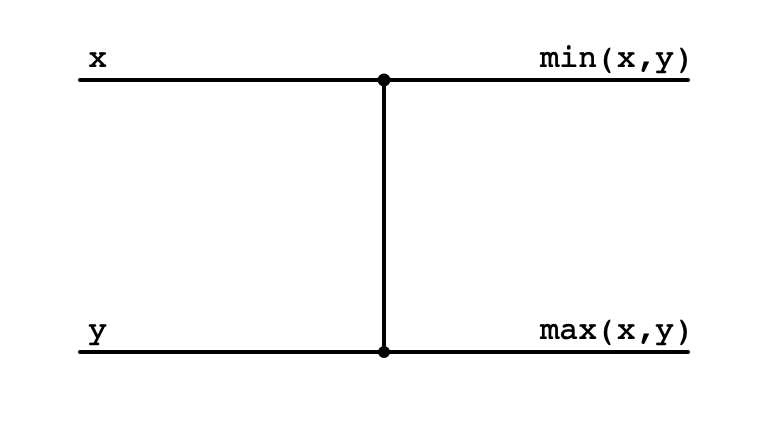
Comparator Swap

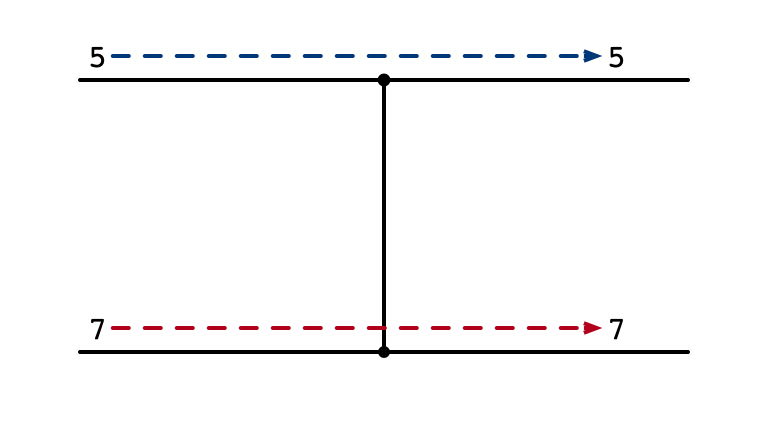
Comparator No Swap

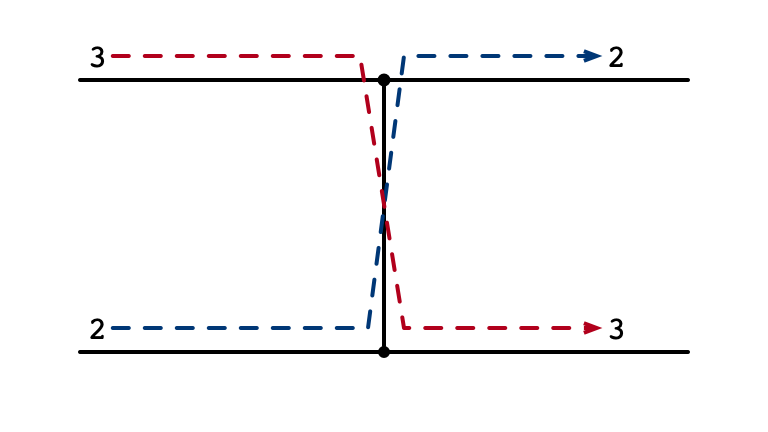
Sorting Array of Two Elements

Insertion Sort

for (int i = 1; i < data.length; ++i) {
    for (int j = i; j > 0; --j) {
        if (data[j-1] > data[j]) {
            swap(data, j-1, j)		
        }
    }
}

Insertion Sort: i = 1

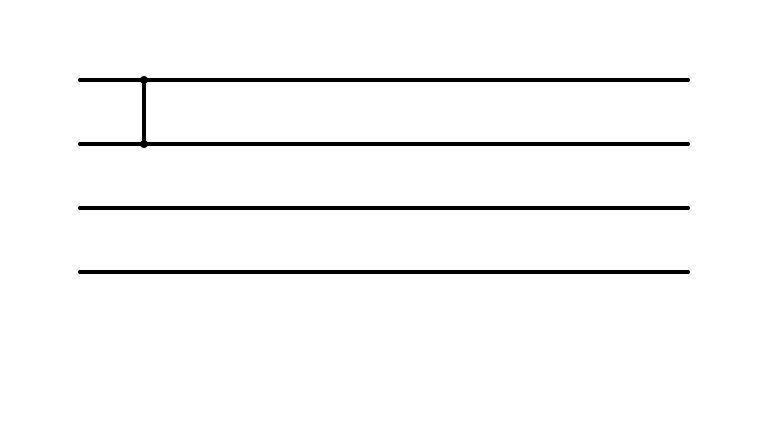
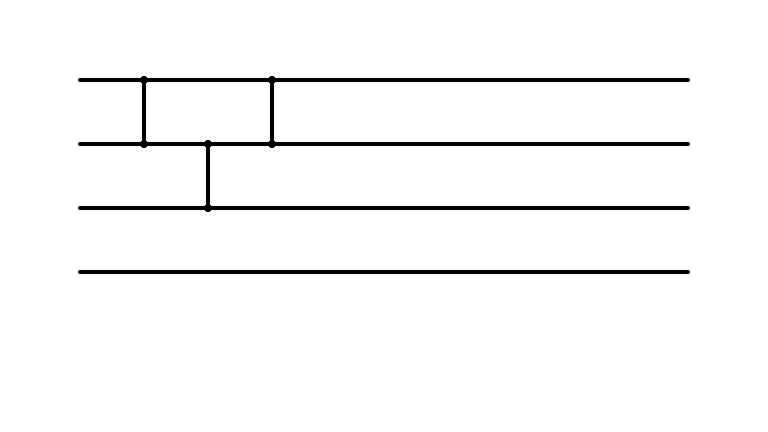
Insertion Sort: i = 2

Insertion Sort: i = 3

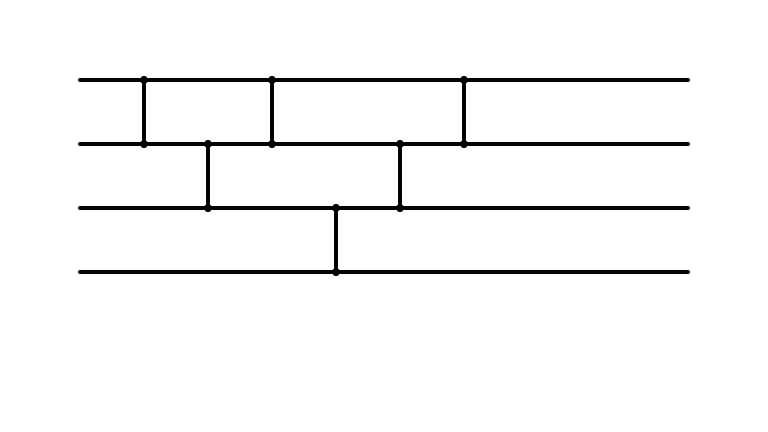
Which Operations can be Parallelized?

Parallelism

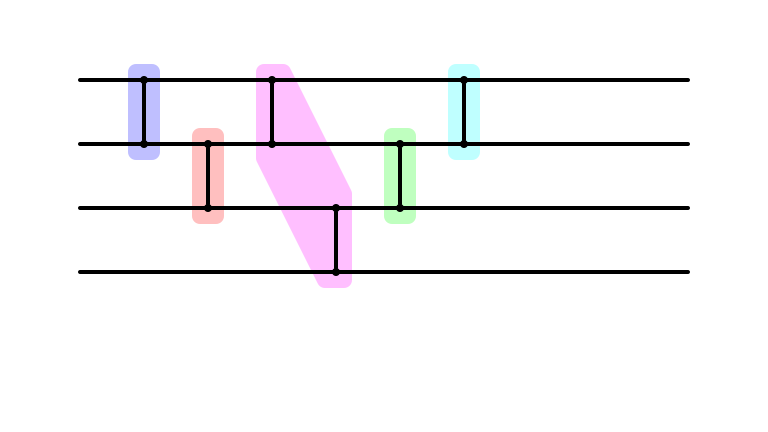
Cleaner Parallel Representation

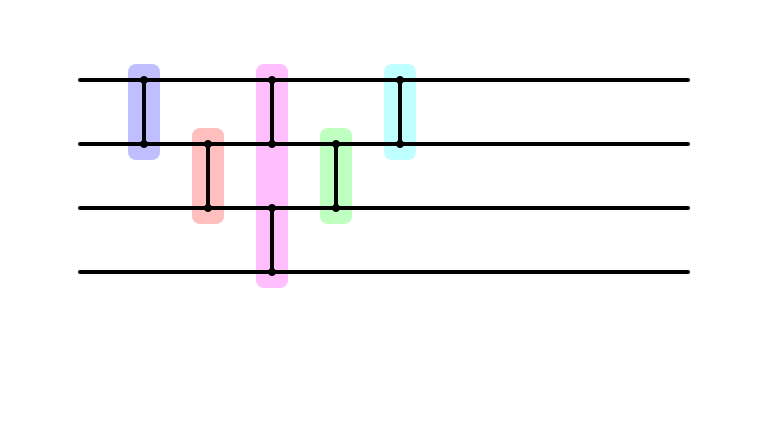
Depth

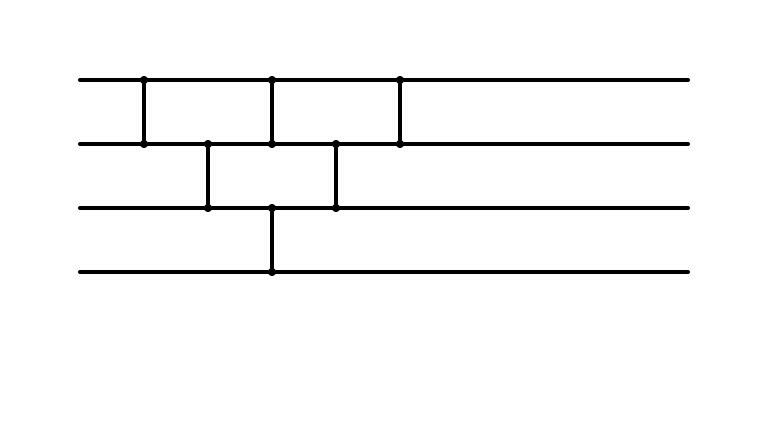
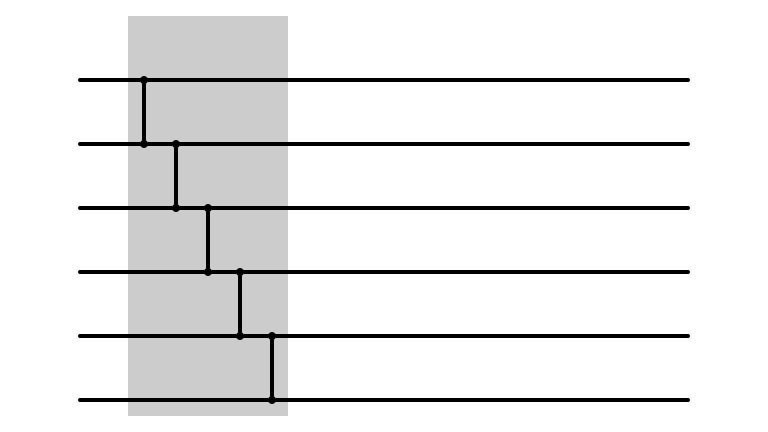
Insertion Sort: Larger Instance

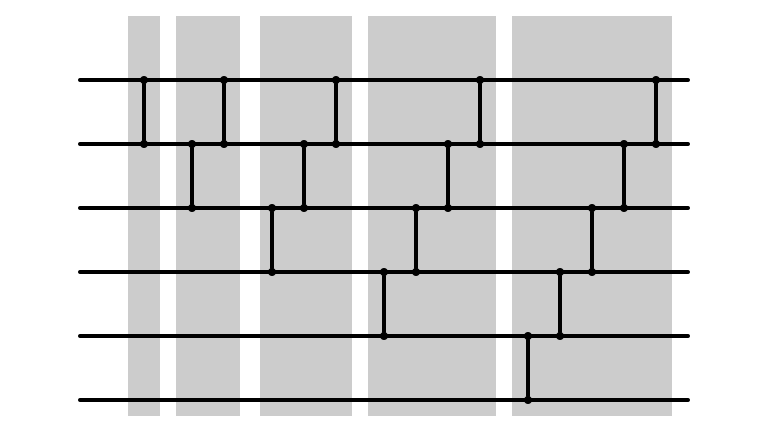
Done In Parallel?

Done In Parallel!

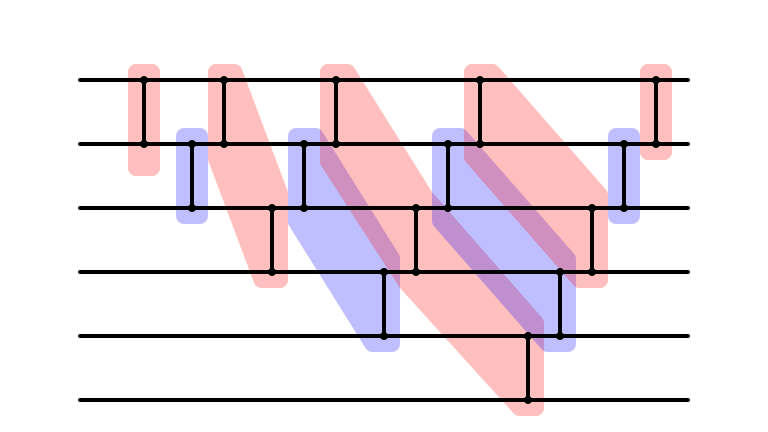
Cleaned Up

Parallel Depth?

Bubble Sort

Consider:

for (int m = data.length - 1; m > 0; --m) {
    for (int i = 0; i < m; ++i) {
        if (data[i] > data[i+1]) {
            swap(data, i, i+1)		
        }
    }
}

Can we make a sorting network corresponding to bubble sort?

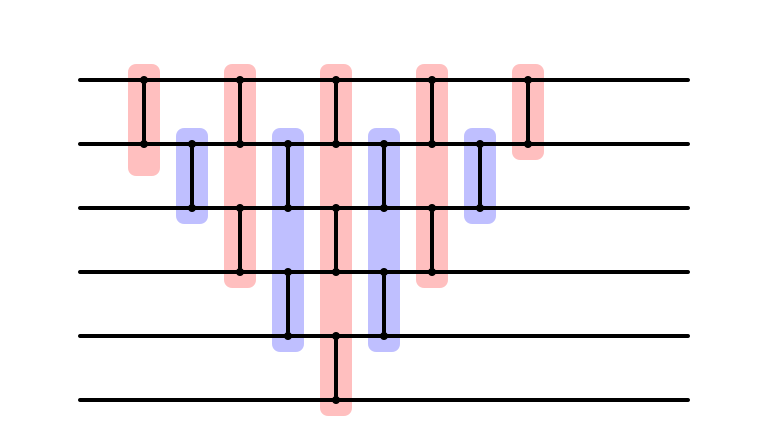
Bubble Sort: m = 6

Bubble Sort: m = 5

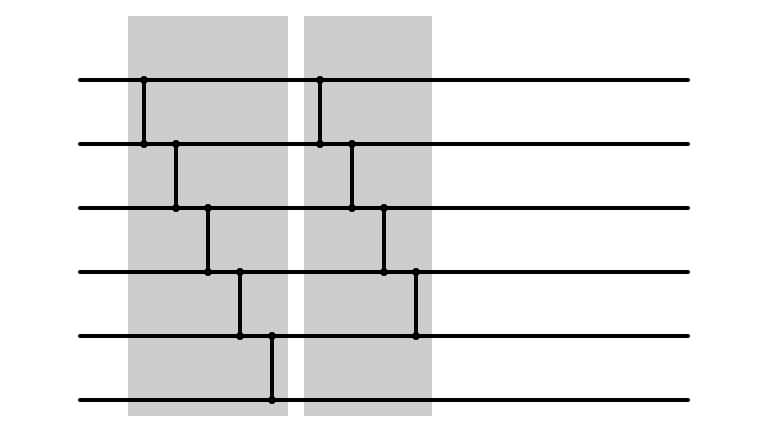
Bubble Sort: m = 4

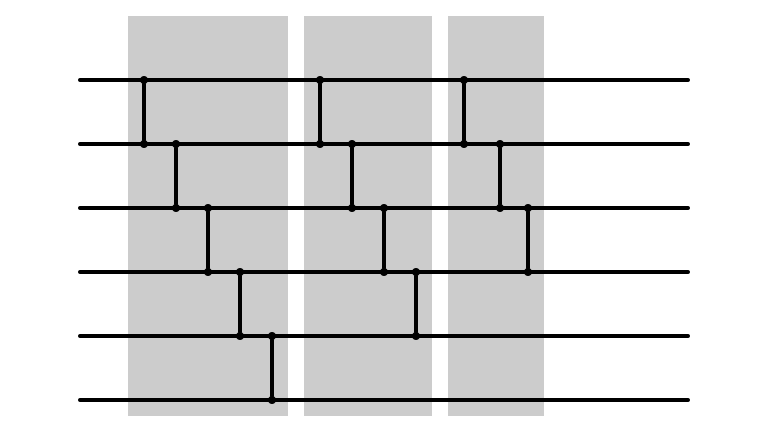
Bubble Sort: m = 3

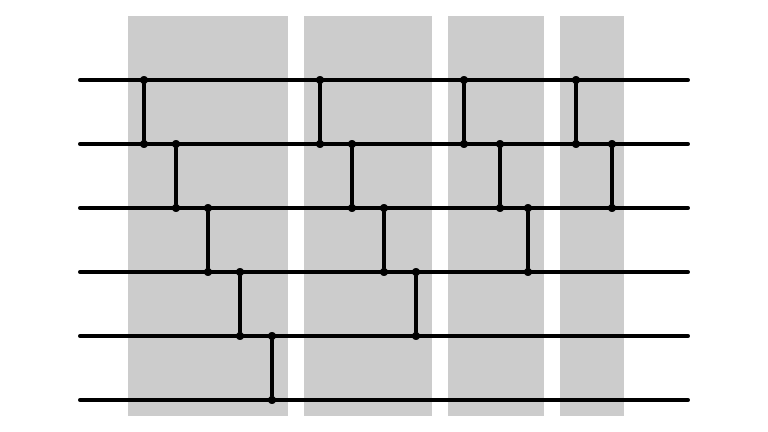
Bubble Sort: m = 2

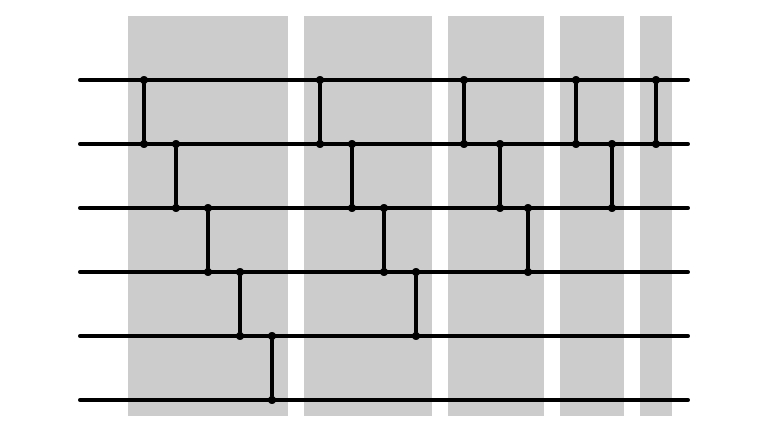
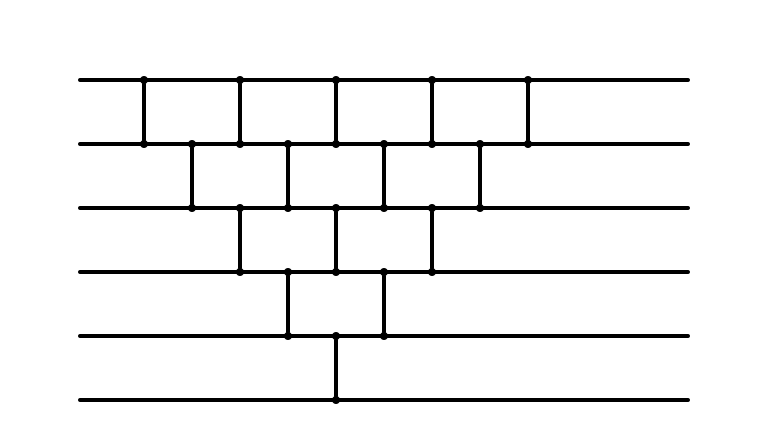
Bubble Sort Network

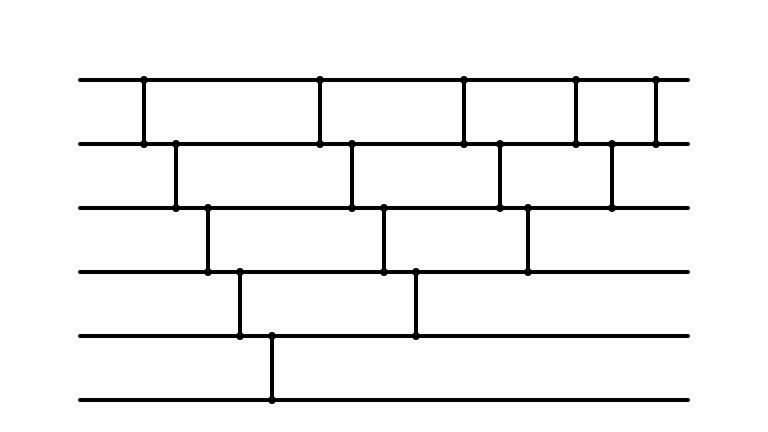
Bubble Sort Parallelized?

Does it Look Familiar?

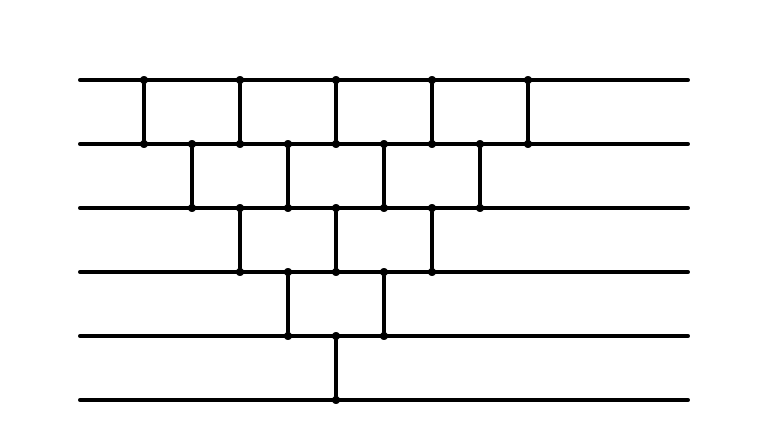
Huh

• Insertion sort and bubble sort perform precisely same operations
  • only differ in the order in which comparisons are made

• When fuly parallelized, both are same sorting network

• Parallel versions are reasonably efficient
  • depth $2 (n - 1) - 1 = 2 n - 3$

Applications

• Sorting networks can be efficiently implemented in hardware
  • can sort fixed number of items much faster than software sorting
• Depth corresponds to latency
  • smaller depth = faster computations

Activity

Find a minimum depth sorting networks for small $n$!

Minimum Depth for $n = 4$?

Smaller Depth for $n = 6$?

Current State

What is known:

• Optimal depth sorting networks for $n \leq 17$

What is not known:

• Optimal depth sorting networks for $n \geq 18$